2.3 Partiell integrering
Förberedande kurs i matematik 2
| Rad 9: | Rad 9: | ||
{{Info| | {{Info| | ||
'''Innehåll:''' | '''Innehåll:''' | ||
| - | * Partiell integration | + | * Partiell integration. |
}} | }} | ||
| Rad 48: | Rad 48: | ||
Det är viktigt att påpeka att metoden inte alltid leder till en integral som är lättare än den ursprungliga. Det kan också vara helt avgörande hur man väljer funktionerna <math>f</math> och <math>g</math>, vilket följande exempel visar. | Det är viktigt att påpeka att metoden inte alltid leder till en integral som är lättare än den ursprungliga. Det kan också vara helt avgörande hur man väljer funktionerna <math>f</math> och <math>g</math>, vilket följande exempel visar. | ||
| + | <div class="exempel"> | ||
| + | '''Exempel 1''' | ||
| - | + | Bestäm integralen <math>\,\int x \cdot \sin x \, dx\,</math>. | |
| + | <br> | ||
| + | <br> | ||
| + | Om man väljer <math>f=x</math> och <math>g=\sin x</math> får man <math>F=x^2/2</math> och <math>g'=\cos x</math>, och enligt formeln för partiell integration | ||
{{Fristående formel||<math>\int x \cdot \sin x \, dx = \frac{x^2}{2} \cdot \sin x - \int \frac{x^2}{2} \cdot \cos x \, dx\,\mbox{.}</math>}} | {{Fristående formel||<math>\int x \cdot \sin x \, dx = \frac{x^2}{2} \cdot \sin x - \int \frac{x^2}{2} \cdot \cos x \, dx\,\mbox{.}</math>}} | ||
| Rad 58: | Rad 63: | ||
{{Fristående formel||<math>\int x \cdot \sin x \, dx = - x \cdot \cos x - \int - 1 \cdot \cos x \, dx = - x\cos x + \sin x + C\,\mbox{.}</math>}} | {{Fristående formel||<math>\int x \cdot \sin x \, dx = - x \cdot \cos x - \int - 1 \cdot \cos x \, dx = - x\cos x + \sin x + C\,\mbox{.}</math>}} | ||
| - | + | </div> | |
<div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel | + | '''Exempel 2''' |
Bestäm integralen <math>\ \int x^2 \cdot \ln x \, dx\,</math>. | Bestäm integralen <math>\ \int x^2 \cdot \ln x \, dx\,</math>. | ||
| Rad 73: | Rad 78: | ||
<div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel | + | '''Exempel 3''' |
Bestäm integralen <math>\ \int x^2 e^x \, dx\,</math>. | Bestäm integralen <math>\ \int x^2 e^x \, dx\,</math>. | ||
| Rad 93: | Rad 98: | ||
<div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel | + | '''Exempel 4''' |
Bestäm integralen <math>\ \int e^x \cos x \, dx\,</math>. | Bestäm integralen <math>\ \int e^x \cos x \, dx\,</math>. | ||
<br> | <br> | ||
<br> | <br> | ||
| - | I en första partiell integrering väljer vi att integrera faktorn <math>e^x</math> och derivera faktorn <math>\cos x</math> | + | I en första partiell integrering väljer vi att integrera faktorn <math>e^x</math> och derivera faktorn <math>\cos x</math>, |
| - | + | ||
| - | + | ||
| - | {{Fristående formel||<math>\int e^x \cos x \, dx = e^x \cos x + \int e^x \sin x \, dx\,\mbox{.}</math>}} | + | {{Fristående formel||<math>\begin{align*}\int e^x \cos x \, dx &= e^x \cdot \cos x - \int e^x \cdot(-\sin x) \, dx\\[10pt] &= e^x \cos x + \int e^x \sin x \, dx\,\mbox{.}\end{align*}</math>}} |
Resultatet blev att vi väsentligen bytte ut faktorn <math>\cos x</math> mot <math>\sin x</math> i integralen. Om vi därför partialintegrerar en gång till (integrera <math>e^x</math> och derivera <math>\sin x</math>) då får vi att | Resultatet blev att vi väsentligen bytte ut faktorn <math>\cos x</math> mot <math>\sin x</math> i integralen. Om vi därför partialintegrerar en gång till (integrera <math>e^x</math> och derivera <math>\sin x</math>) då får vi att | ||
| Rad 121: | Rad 124: | ||
<div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel | + | '''Exempel 5''' |
Beräkna integralen <math>\ \int_{0}^{1} \frac{2x}{e^x} \, dx\,</math>. | Beräkna integralen <math>\ \int_{0}^{1} \frac{2x}{e^x} \, dx\,</math>. | ||
| Rad 137: | Rad 140: | ||
<div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel | + | '''Exempel 6''' |
Beräkna integralen <math>\ \int \ln \sqrt{x} \ dx\,</math>. | Beräkna integralen <math>\ \int \ln \sqrt{x} \ dx\,</math>. | ||
Nuvarande version
| Teori | Övningar |
Innehåll:
- Partiell integration.
Lärandemål:
Efter detta avsnitt ska du ha lärt dig att:
- Förstå härledningen av formeln för partiell integration.
- Lösa integrationsproblem som kräver partiell integration i ett eller två steg.
- Lösa integrationsproblem som kräver partiell integration följt av en substitution (eller tvärt om).
Partiell integration
Vid integrering av produkter kan man ibland använda sig av en metod som kallas partiell integration. Metoden bygger på att man använder deriveringsregeln för produkter baklänges. Om
 g)=f g)=f  g+f g+f g g . . |
Om man nu integrerar båda leden får man
 g= g= (f (f  g+f g+f g g )dx= )dx= f f  gdx+ gdx+ f f g g dx dx |
eller efter ommöblering
 f f  gdx=f gdx=f g− g− f f g g dx. dx. |
Detta ger oss formeln för partiell integration.
Partiell integration:
 f(x) f(x) g(x)dx=F(x) g(x)dx=F(x) g(x)− g(x)− F(x) F(x) g g (x)dx. (x)dx. |
Detta innebär i praktiken att man integrerar en produkt av funktioner genom att kalla den ena faktorn  f
f gdx
gdx  F
F g
g dx,
dx, 
Det är viktigt att påpeka att metoden inte alltid leder till en integral som är lättare än den ursprungliga. Det kan också vara helt avgörande hur man väljer funktionerna
Exempel 1
Bestäm integralen  x
x sinxdx
sinxdx
Om man väljer  2
2 =cosx
=cosx
 x x sinxdx=2x2 sinxdx=2x2 sinx− sinx− 2x2 2x2 cosxdx. cosxdx. |
Den nya integralen i högerledet är i detta fall inte enklare än den ursprungliga integralen.
Om man i stället väljer  =1
=1
 x x sinxdx=−x sinxdx=−x cosx− cosx− −1 −1 cosxdx=−xcosx+sinx+C. cosxdx=−xcosx+sinx+C. |
Exempel 2
Bestäm integralen  x2
x2 lnxdx
lnxdx
Sätt  3
3 =1
=1 x
x
 x2 x2 lnxdx=3x3 lnxdx=3x3 lnx− lnx− 3x3 3x3 x1dx=3x3 x1dx=3x3 lnx−31 lnx−31 x2dx=3x3 x2dx=3x3 lnx−31 lnx−31 3x3+C=31x3(lnx−31)+C. 3x3+C=31x3(lnx−31)+C. |
Exempel 3
Bestäm integralen  x2exdx
x2exdx
Sätt  =2x
=2x
 x2exdx=x2ex− x2exdx=x2ex− 2xexdx. 2xexdx. |
Här krävs ytterligare partiell integration för att lösa den nya integralen  2xexdx
2xexdx  =2
=2
 2xexdx=2xex− 2xexdx=2xex− 2exdx=2xex−2ex+C. 2exdx=2xex−2ex+C. |
Den ursprungliga integralen blir alltså
 x2exdx=x2ex−2xex+2ex+C. x2exdx=x2ex−2xex+2ex+C. |
Exempel 4
Bestäm integralen  excosxdx
excosxdx
I en första partiell integrering väljer vi att integrera faktorn
 excosxdx=ex excosxdx=ex cosx− cosx− ex ex (−sinx)dx=excosx+ (−sinx)dx=excosx+ exsinxdx. exsinxdx. |
Resultatet blev att vi väsentligen bytte ut faktorn
 exsinxdx=exsinx− exsinxdx=exsinx− excosxdx. excosxdx. |
Den ursprungliga integralen dyker här alltså upp igen. Vi får sammantaget:
 excosxdx=excosx+exsinx− excosxdx=excosx+exsinx− excosxdx excosxdx |
och samlar vi integralerna i ena ledet fås att
 excosxdx=21ex(cosx+sinx)+C. excosxdx=21ex(cosx+sinx)+C. |
Trots att de partiella integrationerna i detta fall inte ledde till någon enklare integral kom vi alltså fram till en ekvation där den ursprungliga integralen kunde ”lösas ut”. Detta är inte helt ovanligt när integranden är en produkt av trigonometriska funktioner och/eller exponentialfunktioner.
Exempel 5
Beräkna integralen  01ex2xdx
01ex2xdx
Integralen kan skrivas om som
 01ex2xdx= 01ex2xdx= 012x 012x e−xdx. e−xdx. |
Sätt nu
 012x 012x e−xdx= e−xdx= −2xe−x −2xe−x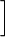 10+ 10+ 012e−xdx= 012e−xdx= −2xe−x −2xe−x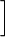 10+ 10+ −2e−x −2e−x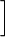 10=(−2 10=(−2 e−1)−0+(−2 e−1)−0+(−2 e−1)−(−2)=−e2−e2+2=2−e4. e−1)−(−2)=−e2−e2+2=2−e4. |
Exempel 6
Beräkna integralen  ln
ln x dx
x dx
Vi utför först en variabelsubstitution  x
x  2
2 x=dx
x=dx 2u
2u
 ln ln xdx= xdx= lnu lnu 2udu. 2udu. |
Sedan partialintegrerar vi. Sätt
 lnu lnu 2udu=u2lnu− 2udu=u2lnu− u2 u2 u1du=u2lnu− u1du=u2lnu− udu=u2lnu−2u2+C=xln udu=u2lnu−2u2+C=xln x−x2+C=x x−x2+C=x ln ln x−21 x−21 +C. +C. |
Anm. Ett alternativt tillvägagångssätt är att skriva om den ursprungliga integranden som  x=21lnx
x=21lnx  lnx
lnx
