Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution 4.3:2b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.3:2b moved to Solution 4.3:2b: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
If we write the angle
 +
<math>\frac{7\pi }{5}</math>
 +
as
 +
 
 +
 
 +
<math>\frac{7\pi }{5}=\frac{5\pi +2\pi }{5}=\pi +\frac{2\pi }{5}</math>
 +
 
 +
 
 +
we see that
 +
<math>\frac{7\pi }{5}</math>
 +
is an angle in the third quadrant.
 +
 
<center> [[Image:4_3_2_b.gif]] </center>
<center> [[Image:4_3_2_b.gif]] </center>
-
<center> [[Image:4_3_2b.gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
the line
 +
<math>x=\cos \frac{7\pi }{5}</math>
 +
 +
The angle between
 +
<math>0</math>
 +
and
 +
<math>\pi </math>
 +
which has the same x-coordinate as the angle
 +
<math>{7\pi }/{5}\;</math>, and hence the same cosine value, is the reflection of the angle
 +
<math>{7\pi }/{5}\;</math>
 +
in the
 +
<math>x</math>
 +
-axis, i.e.
 +
<math>v=\pi -\frac{2\pi }{5}=\frac{3\pi }{5}</math>.

Revision as of 10:34, 29 September 2008

If we write the angle 57 as


57=55+2=+52


we see that 57 is an angle in the third quadrant.

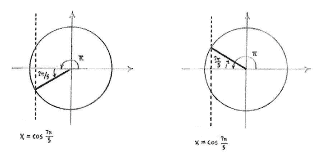
Image:4_3_2_b.gif


the line x=cos57

The angle between 0 and which has the same x-coordinate as the angle 75, and hence the same cosine value, is the reflection of the angle 75 in the x -axis, i.e. v=−52=53.

Retrieved from "http://wiki.math.se/wikis/2009/bridgecourse1-ImperialCollege/index.php/Solution_4.3:2b"