Processing Math: Done
Solution 4.3:3c
From Förberedande kurs i matematik 1
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
| - | With the help of the Pythagorean identity, we can express | + | With the help of the Pythagorean identity, we can express <math>\cos v</math> in terms of <math>\sin v</math>, |
| - | <math>\cos v</math> | + | |
| - | in terms of | + | |
| - | <math>\ | + | |
| + | {{Displayed math||<math>\cos^2 v + \sin^2 v = 1\qquad\Leftrightarrow\qquad \cos v = \pm\sqrt{1-\sin^2 v}\,\textrm{.}</math>}} | ||
| - | <math>\ | + | In addition, we know that the angle <math>v</math> lies between <math>-\pi/2</math> |
| + | and <math>\pi/2</math>, i.e. either in the first or fourth quadrant, where angles always have a positive ''x''-coordinate (cosine value); thus, we can conclude that | ||
| - | + | {{Displayed math||<math>\cos v = \sqrt{1-\sin^2 v} = \sqrt{1-a^2}\,\textrm{.}</math>}} | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | <math>\cos v=\sqrt{1-\ | + | |
Current revision
With the help of the Pythagorean identity, we can express
 cosv= cosv=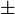 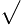 1−sin2v. 1−sin2v. |
In addition, we know that the angle 
 2
2
 2
2
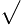 1−sin2v= 1−sin2v=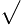 1−a2. 1−a2. |
