3.1 Roots
From Förberedande kurs i matematik 1
Innehåll:
- Kvadratrot och n:te rot
- Rotlagar
Lärandemål:
Efter detta avsnitt ska du ha lärt dig att:
- Skriva om ett rotuttryck i potensform.
- Beräkna kvadratroten ur några enkla heltal.
- Kvadratroten ur ett negativt tal inte är definierad.
- Kvadratroten ur ett tal betecknar den positiva roten.
- Hantera rotlagarna i förenkling av rotuttryck.
- Veta när rotlagarna är giltiga (icke-negativa radikander).
- Förenkla rotuttryck med kvadratrötter i nämnaren.
- Veta när n:te roten ur ett negativt tal är definierad (n udda).
Kvadratrötter
right
Symbolen  a
a
Ekvationen  2=4
2=4 (−2)=4
(−2)=4 4
4  4=
4=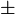 2
2  4
4
Kvadratroten  a
a 
Kvadratroten ur 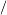 2
2
Det är därför fel att påstå att  4=
4=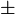 2
2
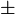 2
2
Exempel 1
 0=0
0=0 02=0 och 0=0
0=00 är inte negativ. 100=10
100=10 102=10 och 10=100
10=10010 är ett positivt tal.-
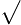 0
0 25=0
25=0 5
5 0 och 52=0
52=0 5
5 0
0 5=0
5=0 25
250 är positiv. 5
5  2
2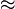 1
1 4142
4142 1 och 4142
4142 1
1 4142
4142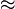 2
21 är positiv. 4142
4142- Ekvationen
x2=2 har lösningarnax= och 2
2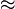 1
1 414
414 x=− . 2
2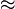 −1
−1 414
414  −4
−4 x som uppfyllerx2=−4 .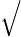 (−7)2=7
(−7)2=7 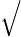 (−7)2=
(−7)2=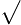 (−7)
(−7) (−7)=
(−7)= 49=
49= 7
7 7=7
7=7
När man räknar med kvadratrötter kan det vara bra att känna till några räkneregler. Eftersom  a=a1
a=a1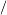 2
2
 9 9 4=(9 4=(9 4)1 4)1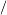 2=91 2=91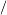 2 2 41 41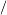 2= 2= 9 9  4. 4. |
På detta sätt kan vi få fram följande räkneregler för kvadratrötter,
som gäller för alla reella tal  b
b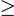 0:
0:
 ab ab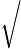 baa baa b= b= a a  b= b= b b a= a=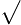 a2b a2b |
(Vi måste dock vid divisionen ovan som vanligt förutsätta att b inte är 0.)
Exempel 2
 64
64 81=
81= 64
64
 81=8
81=8 9=72
9=72 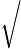 925=
925= 9
9 25=53
25=53  18
18
 2=
2= 18
18 2=
2= 36=6
36=6  3
3 75=
75=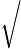 375=
375= 25=5
25=5  12=
12= 4
4 3=
3= 4
4
 3=2
3=2 3
3
Observera att räknereglerna ovan förutsätter att 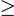 0
0 a
a  b
b
 −1 −1  −1= −1=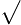 (−1) (−1) (−1)= (−1)= 1=1 1=1 |
men ser då att något inte stämmer. Anledningen är att  −1
−1
Högre ordningars rötter
Kubikroten ur ett tal  3a
3a
Exempel 3
 38=2
38=2 2 . 2
2 2=8
2=8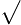 30
30 027=0
027=0 3
3 0 . 3
3 0
0 3
3 0
0 3=0
3=0 027
027 3−8=−2
3−8=−2 (−2) . (−2)
(−2) (−2)=−8
(−2)=−8
Notera att, till skillnad från kvadratrötter, är kubikrötter även definierade för negativa tal.
Det går sedan att för positiva heltal
- om
n är jämn ocha är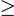 0
0 na
na n gånger blira , - om
n är udda så är na
na n gånger blira .
Roten  na
na 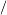 n
n
Exempel 4
 4625=5
4625=5 5 . 5
5 5
5 5=625
5=625 5−243=−3
5−243=−3 (−3) . (−3)
(−3) (−3)
(−3) (−3)
(−3) (−3)=−243
(−3)=−243 6−17
6−17 6 är jämn och−17 är ett negativt tal.
För  b
b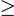 0
0
 nab nab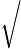 nbaa nbaa nb= nb= na na  nb= nb= nb nb na= na= nanb nanb |
Förenkling av rotuttryck
Ofta kan man genom att använda räknereglerna för rötter förenkla rotuttryck väsentligt. Liksom vid potensräkning handlar det ofta om att bryta ner uttryck i så "små" rötter som möjligt. Exempelvis gör man gärna omskrivningen
 8= 8= 4 4 2= 2= 4 4  2=2 2=2 2 2 |
eftersom man då kan förenkla t.ex.
 8=22 8=22 2= 2= 2. 2. |
Genom att skriva rotuttryck i termer av "små" rötter kan man också addera rötter av "samma sort", t.ex.
 8+ 8+ 2=2 2=2 2+ 2+ 2=(2+1) 2=(2+1) 2=3 2=3 2. 2. |
Exempel 5
 8
8 18=
18= 2
2 9
9 2
2 4=
4= 2
2 3
3 3
3 2
2 2
2 2=
2=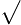 2
2 32
32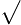 2
2 22=3
22=3 22
22 2=32
2=326  72=2
72=2 3
3 8
8 9=2
9=2 3
3 2
2 2
2 2
2 3
3 3=2
3=2 3
3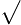 22
22 32
32 2=2
2=2 32
32 3
3 2=
2= 2
2  45+
45+ 20=
20= 9
9 5+
5+ 4
4 5=
5=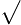 32
32 5+
5+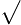 22
22 5=3
5=3 5+2
5+2 5
5
=(3+2)  5=5
5=5 5
5  50+2
50+2 3−
3− 32+
32+ 27=
27= 5
5 10+2
10+2 3−
3− 2
2 16+
16+ 3
3 9
9
=  5
5 2
2 5+2
5+2 3−
3− 2
2 4
4 4+
4+ 3
3 3
3 3
3
= 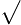 52
52 2+2
2+2 3−
3−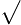 22
22 22
22 2+
2+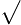 3
3 32
32
=5  2+2
2+2 3−2
3−2 2
2 2+3
2+3 3
3
=(5−4)  2+(2+3)
2+(2+3) 3
3
=  2+5
2+5 3
3  3122
3122
 33=
33= 33
33 42
42
 33=2
33=2
 33
33 33
33
 34=2
34=2 34=2
34=2 32
32 2=2
2=2 32
32
 32
32
 32
32 32=22
32=22
 32=
32= 32
32(  3+
3+ 2)(
2)( 3−
3− 2)=(
2)=( 3)2−(
3)2−( 2)2=3−2=1
2)2=3−2=1 - där vi använt konjugatregeln
(a+b)(a−b)=a2−b2 med \displaystyle a=\sqrt{3} och \displaystyle b=\sqrt{2}.
- där vi använt konjugatregeln
Rationella rotuttryck
När rötter förekommer i ett rationellt uttryck vill man ofta undvika rötter i nämnaren (eftersom det är svårt vid handräkning att dividera med irrationella tal). Genom att förlänga med \displaystyle \sqrt{2} kan man exempelvis göra omskrivningen
\displaystyle \frac{1}{\sqrt{2}}
= \frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}
= \frac{\sqrt{2}}{2}
|
vilket oftast är att föredra.
I andra fall kan man utnyttja konjugatregeln, \displaystyle (a+b)(a-b) = a^2 - b^2, och förlänga med nämnarens s.k. konjugerade uttryck. På så sätt försvinner rottecknen från nämnaren genom kvadreringen, t.ex.
\displaystyle \begin{align*}
\frac{\sqrt{3}}{\sqrt{2}+1}
&= \frac{\sqrt{3}}{\sqrt{2}+1} \cdot \frac{\sqrt{2}-1}{\sqrt{2}-1}
= \frac{\sqrt{3}\,(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}\\[4pt]
&= \frac{\sqrt{3}\cdot\sqrt{2} - \sqrt{3}\cdot1}{(\sqrt{2}\,)^2 - 1^2 }
= \frac{\sqrt{3 \cdot 2} - \sqrt{3}}{ 2 - 1 }
= \frac{\sqrt{6} - \sqrt{3}}{ 1 }
= \sqrt{6} - \sqrt{3}\mbox{.}
\end{align*}
|
Exempel 6
- \displaystyle \frac{10\sqrt{3}}{\sqrt{5}} = \frac{10\sqrt{3}\cdot\sqrt{5}}{\sqrt{5}\cdot\sqrt{5}} = \frac{10\sqrt{15}}{5} = 2\sqrt{15}
- \displaystyle \frac{1+\sqrt{3}}{\sqrt{2}} = \frac{(1+\sqrt{3})\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} = \frac{\sqrt{2}+\sqrt{6}}{2}
- \displaystyle \frac{3}{\sqrt{2}-2} = \frac{3(\sqrt{2}+2)}{(\sqrt{2}-2)(\sqrt{2}+2)} = \frac{3\sqrt{2}+6}{(\sqrt{2}\,)^2-2^2} = \frac{3\sqrt{2}+6}{2-4} = -\frac{3\sqrt{2}+6}{2}
- \displaystyle \frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}
= \frac{\sqrt{2}\,(\sqrt{6}-\sqrt{3}\,)}{(\sqrt{6}+\sqrt{3}\,)
(\sqrt{6}-\sqrt{3}\,)}
= \frac{\sqrt{2}\,\sqrt{6}-\sqrt{2}\,\sqrt{3}}{(\sqrt{6}\,)^2
-(\sqrt{3}\,)^2}\vphantom{\Biggl(}
\displaystyle \phantom{\frac{\sqrt{2}}{\sqrt{6}+\sqrt{3}}\vphantom{\Biggl(}}{} = \frac{\sqrt{2}\,\sqrt{2\cdot 3}-\sqrt{2}\,\sqrt{3}}{6-3} = \frac{2\sqrt{3}-\sqrt{2}\,\sqrt{3}}{3} = \frac{(2-\sqrt{2}\,)\sqrt{3}}{3} \vphantom{\displaystyle\frac{a^{\textstyle b^{\textstyle c}}}{b}}
Råd för inläsning
Grund- och slutprov
Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
Tänk på att:
Kvadratroten ur ett tal är alltid icke-negativ (dvs. positiv eller lika med noll)!
Rotlagarna är egentligen specialfall av potenslagarna.
Exempelvis: \displaystyle \sqrt{x}=x^{1/2}.
Lästips
För dig som vill fördjupa dig ytterligare eller behöver en längre förklaring
Läs mer om kvadratrötter i engelska Wikipedia
Hur vet man att roten ur 2 inte är ett bråktal?
Länktips
