Inlämningsuppgift

Matematik för naturvetare 15hp

Versionen från 20 september 2007 kl. 14.48 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring		Nuvarande version (20 september 2007 kl. 15.44) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag)
(7 mellanliggande versioner visas inte.)
Rad 22:		Rad 22:
	$\displaystyle{ \left\{ \begin{matrix} \log_x \left( y+\frac{y^2}{4} \right) &=& 3 \\ \log_y ( x^2) &=& 1 \end{matrix} \right. }$		$\displaystyle{ \left\{ \begin{matrix} \log_x \left( y+\frac{y^2}{4} \right) &=& 3 \\ \log_y ( x^2) &=& 1 \end{matrix} \right. }$
		+
		+
		+
		+	==Uppgift 4==
		+
		+	Lös matrisekvationen
		+
		+	$$AX=B$$
		+
		+	där $X$ är en matris av typ $2\times2$ och
		+
		+	$$A=\pmatrix{1&2\\3&4}$$
		+	$$B=\pmatrix{1&1\\5&1}$$
		+
		+
		+
		+	==Uppgift 5==
		+
		+	En viss fakultet har tre sorters studenter; matematikstuderande, fysiker samt de som inte studerar något alls.
		+	Antalet studenter i respektive grupp kallar vi $S_1$, $S_2$ och $S_3$.
		+
		+
		+	Varje år så tar 10% av matematikerna och 20% av fysikerna paus och slutar studera (men är kvar på fakulteten),
		+	och det tillkommer 20% till matematikerna och 40% till fysikerna från de som inte studerar.
		+	Dessutom så inser vissa fysiker att matematik är jätteviktigt, så 20% av fysikerna flyttar över till
		+	matematiklinjen.
		+
		+	Vi kan beskriva detta med hjälp av en övergångsmatris $A$ så att $X_{t+1} = AX_t$ där $X_0 = \pmatrix{S_1\\S_2\\S_3}$.
		+
		+	'''a)'''
		+
		+	Bestäm $A$
		+
		+
		+	Antag att vi har $S_1=100$ matematikstudenter, $S_2=200$ fysikstudenter samt $S_3=50$ studenter som inte studerar.
		+
		+
		+	'''b)'''
		+
		+	Hur är fördelningen efter ett år?
		+
		+
		+	'''c)'''
		+
		+	Hur är fördelningen efter 10 år? (Avrunda till närmaste heltal.)
		+
		+
		+	'''d)'''
		+
		+	Undersök om det finns någon stabil fördelning och bestäm denna i så fall.

---

Nuvarande version

Dessa inlämningsuppgifter är en del av examinationen av momentet "Linjär algebra, 3 hp". Du kan lösa uppgifterna när som helst, men för att kunna lämna in ett lösningsförslag så måste samtliga grundprov och slutprov för Dag 7 - Dag 10 vara godkända. Efter att du lämnat in ett lösningsförslag så kommer du att grupperas med två andra (det kan ta lite tid) och ni skall sedan titta på varandras lösningar och i ett gruppforum diskutera er fram till en gemnsam gruppinlämning.

Innehåll 1 Uppgift 1 2 Uppgift 2 3 Uppgift 3 4 Uppgift 4 5 Uppgift 5

[redigera] Uppgift 1

Använd t.ex. de Moivres formel och binomialteoremet för att härleda en formel som uttrycker $\cos5x$ som ett polynom i $\cos x$, eller mer precist bestäm konstanterna $A,B,C$ så att $\cos 5x=A(\cos x)^5+B(\cos x)^3+C\cos x$

[redigera] Uppgift 2

Låt $x,y,z$ vara tre reella tal som är sinsemellan olika, dvs $x\ne y$ $x\ne z$ $y\ne z$. Visa att

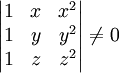
[redigera] Uppgift 3

Lös ekvationssystemet

$\displaystyle{ \left\{ \begin{matrix} \log_x \left( y+\frac{y^2}{4} \right) &=& 3 \\ \log_y ( x^2) &=& 1 \end{matrix} \right. }$

[redigera] Uppgift 4

Lös matrisekvationen

$$AX=B$$

där $X$ är en matris av typ $2\times2$ och

$$A=\pmatrix{1&2\\3&4}$$ $$B=\pmatrix{1&1\\5&1}$$

[redigera] Uppgift 5

En viss fakultet har tre sorters studenter; matematikstuderande, fysiker samt de som inte studerar något alls. Antalet studenter i respektive grupp kallar vi $S_1$, $S_2$ och $S_3$.

Varje år så tar 10% av matematikerna och 20% av fysikerna paus och slutar studera (men är kvar på fakulteten), och det tillkommer 20% till matematikerna och 40% till fysikerna från de som inte studerar. Dessutom så inser vissa fysiker att matematik är jätteviktigt, så 20% av fysikerna flyttar över till matematiklinjen.

Vi kan beskriva detta med hjälp av en övergångsmatris $A$ så att $X_{t+1} = AX_t$ där $X_0 = \pmatrix{S_1\\S_2\\S_3}$.

a)

Bestäm $A$

Antag att vi har $S_1=100$ matematikstudenter, $S_2=200$ fysikstudenter samt $S_3=50$ studenter som inte studerar.

b)

Hur är fördelningen efter ett år?

c)

Hur är fördelningen efter 10 år? (Avrunda till närmaste heltal.)

d)

Undersök om det finns någon stabil fördelning och bestäm denna i så fall.