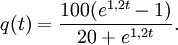Lösningar 20
Matematik för naturvetare 15hp
| Versionen från 2 oktober 2007 kl. 13.35 (redigera) Clas Löfwall (Diskussion | bidrag) (Ny sida: ==Lösningar till några övningar till lektion 20== Tillbaka till lösningarna) ← Gå till föregående ändring |
Versionen från 26 oktober 2007 kl. 10.27 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 1: | Rad 1: | ||
| ==Lösningar till några övningar till lektion 20== | ==Lösningar till några övningar till lektion 20== | ||
| + | |||
| + | |||
| + | 13.2. Ekvationen har separabla variabler och kan skrivas | ||
| + | $e^{-y}y'=-2x$, vilken kan skrivas <math> | ||
| + | \frac{d}{dx}(-e^{-y})=\frac{d}{dx}(-x^2),</math> | ||
| + | som ger $e^{-y}=x^2+C$, där $C$ är en konstant. Alltså är | ||
| + | $y=-\ln(x^2+C)$. Sätter vi $x=0$ så får vi $0=-\ln C$, varav $C=1$. | ||
| + | Lösningen är således $y=-\ln(x^2+1)$. | ||
| + | |||
| + | |||
| + | |||
| + | 13.4. Separation av variablerna ger $y'/(1-y)=x$, som kan skrivas | ||
| + | $D(-\ln(1-y))=D(x^2/2)$, där $D$ står för derivatan med avseende på | ||
| + | $x$. Alltså är $\ln(1-y)=-x^2/2+D$, där $D$ är en konstant, varav | ||
| + | $y=1-e^{-x^2/2+D}=1-Ce^{-x^2/2}$, där $C=e^{D}$. Villkoret $y(0)=0$ | ||
| + | ger $C=1$, så att $y=1-e^{-x^2/2}$. | ||
| + | |||
| + | |||
| + | |||
| + | 13.6. Separation av variablerna ger $y'/(1+y^2)=1/\tan x=\cos x/\sin x$. | ||
| + | En primitiv funktion till HL är $\ln|\sin x|$ och vi får $\arctan | ||
| + | y=\ln|\sin x|+C$. Villkoret $y(¹/2)=1$ ger $\arctan 1=\ln 1+C$, så | ||
| + | att $C=¹/4$. Lösningen är $y=\tan(¹/4+\ln|\sin x|)$. | ||
| + | |||
| + | |||
| + | |||
| + | 13.8. Vi har $v(t)=h'(t)$ och får DE:n $h'(t)=0,012h(t)$. Lösningen | ||
| + | är $h(t)=Ce^{0,012t}$. Enligt texten är $h(0)=1$ cm, så | ||
| + | $h(t)=e^{0,012t}$ cm, där tiden $t$ mäts i timmar. Ekvationen | ||
| + | $205=e^{0,012t}$ har lösningen $t\approx 440$ timmar. | ||
| + | |||
| + | |||
| + | |||
| + | 13.10.a. Låt $T(t)$ vara temperaturen som funktion av tiden $t$ efter | ||
| + | bullens uttagande från ugnen. Om rumstemperaturen är $T_{r}$ så får vi | ||
| + | DE:n $T'(t)=k(T(t)-T_{r})$. Separation av variablerna ger | ||
| + | $T'(t)/(T(t)-T_{r})=k$, varav $\ln(T(t)-T_{r})=kt+D$. Detta ger | ||
| + | $T(t)=T_{r}+e^{kt+D}=T_{r}+Ce^{kt}$. Vi har $T(0)=200$, så $200=20+C$, | ||
| + | varav $C=180$. Vidare är $152=20+180e^{k\cdot 1}$ om vi mäter $t$ i | ||
| + | minuter. Härav $k=\ln(132/180)\approx -0,31$, så att <math> | ||
| + | T(t)=20+180e^{-0,31t}.</math> | ||
| + | |||
| + | |||
| + | |||
| + | b. Vi får ekvationen $20+180e^{-0,31t}=35$, som ger | ||
| + | $t=(\ln(15/180))/(-0,31)\approx 8$ minuter. | ||
| + | |||
| + | |||
| + | |||
| + | 13.35. Här måste det vara ett litet fel i texten: Rimligen är det | ||
| + | $b+q$ som är koncentrationen av B efter tiden $t$. | ||
| + | Separation av variablerna ger <math> | ||
| + | \frac{q'(t)}{(a-q)(b+q)}=k.</math> | ||
| + | Partialbråksuppdelning av VL ger <math> | ||
| + | \frac{1}{a+b}\left(\frac{1}{a-q}+\frac{1}{b+q}\right)q'(t)=k</math> | ||
| + | varför <math> | ||
| + | -\ln(a-q)+\ln(b+q)=k(a+b)t+C=Kt+C.</math> | ||
| + | När $t=0$ är $q=0$, så $C=-\ln a+\ln b=\ln (b/a)=\ln (5/100)=-\ln | ||
| + | 20$. För $t=1$ är $q=10$, så $-\ln(100-10)+\ln(5+10)=K\cdot 1-\ln 20$, | ||
| + | varav $K=\ln 20-\ln 90+\ln 15=\ln(300/90)=\ln(10/3)\approx 1,2$. Löser | ||
| + | vi ekvationen <math> | ||
| + | \frac{5+q}{100-q}=0,05e^{1,2t}</math> | ||
| + | så får vi <math> | ||
| + | q(t)=\frac{100(e^{1,2t}-1)}{20+e^{1,2t}}.</math> | ||
| + | |||
| + | |||
| + | |||
| [[Exempellösningar|Tillbaka till lösningarna]] | [[Exempellösningar|Tillbaka till lösningarna]] | ||
Versionen från 26 oktober 2007 kl. 10.27
Lösningar till några övningar till lektion 20
13.2. Ekvationen har separabla variabler och kan skrivas
$e^{-y}y'=-2x$, vilken kan skrivas 
som ger $e^{-y}=x^2+C$, där $C$ är en konstant. Alltså är
$y=-\ln(x^2+C)$. Sätter vi $x=0$ så får vi $0=-\ln C$, varav $C=1$.
Lösningen är således $y=-\ln(x^2+1)$.
13.4. Separation av variablerna ger $y'/(1-y)=x$, som kan skrivas $D(-\ln(1-y))=D(x^2/2)$, där $D$ står för derivatan med avseende på $x$. Alltså är $\ln(1-y)=-x^2/2+D$, där $D$ är en konstant, varav $y=1-e^{-x^2/2+D}=1-Ce^{-x^2/2}$, där $C=e^{D}$. Villkoret $y(0)=0$ ger $C=1$, så att $y=1-e^{-x^2/2}$.
13.6. Separation av variablerna ger $y'/(1+y^2)=1/\tan x=\cos x/\sin x$. En primitiv funktion till HL är $\ln|\sin x|$ och vi får $\arctan y=\ln|\sin x|+C$. Villkoret $y(¹/2)=1$ ger $\arctan 1=\ln 1+C$, så att $C=¹/4$. Lösningen är $y=\tan(¹/4+\ln|\sin x|)$.
13.8. Vi har $v(t)=h'(t)$ och får DE:n $h'(t)=0,012h(t)$. Lösningen är $h(t)=Ce^{0,012t}$. Enligt texten är $h(0)=1$ cm, så $h(t)=e^{0,012t}$ cm, där tiden $t$ mäts i timmar. Ekvationen $205=e^{0,012t}$ har lösningen $t\approx 440$ timmar.
13.10.a. Låt $T(t)$ vara temperaturen som funktion av tiden $t$ efter bullens uttagande från ugnen. Om rumstemperaturen är $T_{r}$ så får vi DE:n $T'(t)=k(T(t)-T_{r})$. Separation av variablerna ger $T'(t)/(T(t)-T_{r})=k$, varav $\ln(T(t)-T_{r})=kt+D$. Detta ger $T(t)=T_{r}+e^{kt+D}=T_{r}+Ce^{kt}$. Vi har $T(0)=200$, så $200=20+C$, varav $C=180$. Vidare är $152=20+180e^{k\cdot 1}$ om vi mäter $t$ i minuter. Härav $k=\ln(132/180)\approx -0,31$, så att T(t) = 20 + 180e − 0,31t.
b. Vi får ekvationen $20+180e^{-0,31t}=35$, som ger $t=(\ln(15/180))/(-0,31)\approx 8$ minuter.
13.35. Här måste det vara ett litet fel i texten: Rimligen är det
$b+q$ som är koncentrationen av B efter tiden $t$.
Separation av variablerna ger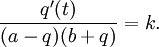 
Partialbråksuppdelning av VL ger 
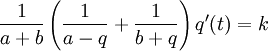varför − ln(a − q) + ln(b + q) = k(a + b)t + C = Kt + C.
När $t=0$ är $q=0$, så $C=-\ln a+\ln b=\ln (b/a)=\ln (5/100)=-\ln
20$. För $t=1$ är $q=10$, så $-\ln(100-10)+\ln(5+10)=K\cdot 1-\ln 20$,
varav $K=\ln 20-\ln 90+\ln 15=\ln(300/90)=\ln(10/3)\approx 1,2$. Löser
vi ekvationen 
så får vi 
