Lösningar 7

Matematik för naturvetare 15hp

---

Versionen från 24 augusti 2007 kl. 19.08

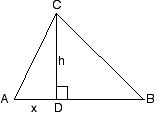
4.22. För den som inte har sett cosinussatsen tidigare (eller glömt den) kommer här ett bevis. I triangeln $\triangle ABC$ nedan har vi dragit höjden från hörnet $C$ mot sidan $AB$. Beteckna fotpunkten med $D$ och sätt $h=|CD|$, $x=|AD|$. Pythagoras sats på de två rätvinkliga trianglarna $\triangle ADC$ och $\triangle DBC$ ger $b^2=h^2+x^2$ respektive $a^2=h^2+(c-x)^2$. Alltså får vi

$a^2=b^2-x^2+(c-x)^2=b^2+c^2-2cx.$

Men enligt "triangeldefinitionen" av cosinus är $\cos A=|AD|/|AC|=x/b$, så $x=b\cos A$ och insättning ger

$a^2=b^2+c^2-2bc\cos A.$

Om fotpunkten $D$ för höjden från $C$ inte ligger mellan $A$ och $B$ (vilket är fallet då $A$ eller $B$ är trubbig), så får man modifiera beviset en smula, men det får du göra själv!

4.23. Sätt in definitionen av tangens.

4.25.

$\frac{1-\cos^2x}{\sin 2x}=\frac{\sin^2x}{2\sin x\cos x}=\frac{\sin x}{2\cos x}=\frac{1}{2}\,\tan x$

enligt trigonometriska ettan och formeln för dubbla vinkeln för sinus.

4.26. Ett uttryck av formen $a\sin x+b\cos x$ kan man alltid skriva om på formen $A\sin(x+\alpha)$ för några tal $A$ och $\alpha$. Den här typen av omskrivningar är viktiga i bl a vågrörelseläran och vi går därför igenom den här. Additionsformeln ger

$A\sin(x+\alpha)=(A\cos\alpha)\sin x+(A\sin\alpha)\cos x,$

så vi vill hitta $A$ och $\alpha$ så att $A\cos\alpha=a,\quad A\sin\alpha=b$. Den trigonometriska ettan ger

$A^2=A^2(\cos^2\alpha+\sin^2\alpha)=(A\cos\alpha)^2+(A\sin\alpha)^2=a^2+b^2,$

dvs $A=±\sqrt{a^2+b^2}$. Normalt väljer man här plustecknet och när man har bestämt $A$ så får man $\alpha$ ur sambanden $\cos\alpha=a/A,\sin\alpha=b/A$. En funktion av formen $f(x)=a\sin x+b\cos x$ är alltså en något modifierad sinusvåg. Talen $A$ och $\alpha$ kallas amplitud respektive fas. Lägg märke till att amplituden betyder det största värde som $f(x)$ kan anta. Fasen betyder hur mycket förskjuten sinusvågen $f(x)$ är i förhållande till den "enkla" vågen $y=\sin x$.

I fallet $\sin x+\cos x$ är $a=b=1$, så $A=\sqrt{1^2+1^2}=\sqrt 2$. Fasen $\alpha$ bestäms ur $\cos\alpha=\sin\alpha=1/\sqrt 2$, som ger $\alpha=\pi/4$ (det finns förstås oändligt många lösningar, men det räcker att ta en av dem, t ex den som ligger mellan 0 och $2\pi$).

4.30. Använder vi formeln för dubbla vinkeln så får vi ekvationen

$2\sin x\cos^2x=2\sin^3x,\quad\mbox{dvs}\quad \sin x(\cos^2x-\sin^2x)=0.$

Detta ger $\sin x=0$ eller $\cos^2x-\sin^2x=0$. Den förra ekvationen har lösningarna $x=n\pi$ och den senare löser man enklast genom att skriva den som $\cos 2x=0$, som ger $2x=\pi/2+n\pi$, dvs $x=\pi/4+n\pi/2$.

En anmärking: När man har kommit till $2\sin x\cos^2x=2\sin^3x$ så är det lätt hänt att man förkortar med $2\sin x$ och får ekvationen $\cos^2x=\sin^2x$. Förkortningen är helt i sin ordning om $\sin x\not=0$, men om $\sin x=0$ så innebär den division med 0. Var alltid försiktig vid division med uttryck som kan vara 0!

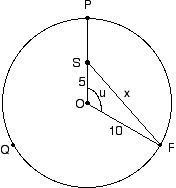
4.31. I figuren nedan är $P$ den punkt där fågeln fångar flugan, $Q$ den punkt där flugan är när fågeln börjar flyga och $R$ den punkt där den är när fågeln flugit 5 m, då den befinner sig i $S$. Punkten $O$ är cirkelns medelpunkt, dvs den punkt där flugsnapparen sitter från början. Det är alltsä längden $x$ av sträckan $SR$ vi skall beräkna.

Eftersom flugan flyger hälften så fort som fågeln, så är bågen $QP$ hälften så lång som sträckan $OP$, dvs 5 m. Alltså är bågen $RP$ $5/2$ m och vinkeln $u=\wedge QOR=(5/2)/10=1/4$ (radianer). Cosinussatsen ger

$x^2=5^2+10^2-2\cdot 5\cdot 10\cdot\cos (1/4),\quad\mbox{varav} \quad x\approx 5,3 \quad\mbox{meter.}$

Här är en anmärkning om radianmåttet på sin plats! Att en vinkel har måttet $\alpha$ radianer innebär att den på enhetscirkeln upptar en båge som är $\alpha$ längdenheter lång. Om man i stället placerar vinkeln med spetsen i medelpunkten i en cirkel med radie $r$, så blir motsvarande båge $r\alpha$.

4.33.c) Svaret är inte $5\pi/3$, som man kanske skulle tro i förstone. Vi har ju nämligen $a=\tan x$ om och endast om $x=\arctan a$ och $-\pi/2<x<\pi/2$. Nu är ju $5\pi/3=2\pi -\pi/3$, så $\tan (5\pi/3)=\tan(-\pi/3)$ och då $-\pi/2<-\pi/3<\pi/2$, så att $\arctan(\tan(5\pi/3))=\arctan(\tan(-\pi/3))=-\pi/3$.

e) Vi har $\sin(-3\pi/4)=\cos(\pi/2-(-3\pi/4))=\cos(5\pi/4)$ och $a=\cos x$ om och endast om $x=\arccos x$ och $0\le x\le \pi$. Talet $5\pi/4$ ligger utanför det här intervallet, men $\cos(5\pi/4)=\cos(2\pi-3\pi/4)=\cos(-3\pi/4)=\cos(3\pi/4)$, där $0\le 3\pi/4\le \pi$. Alltså är $\arccos(\sin(-3\pi/4))=\arccos(\cos(3\pi/4))=3\pi/4$.

f) Observera att $a=\sin x$ om och endast om $x=\arcsin x$ och $-\pi/2\le x\le \pi/2$. Vi har $\sin(8\pi/3)=\sin(2\pi/3+2\pi)=\sin(2\pi/3)=\sin(\pi-\pi/3)=\sin(\pi/3)$, så att $\arcsin(\sin(8\pi/3))=\arcsin(\sin(\pi/3))=\pi/3$.

4.34. För att $\arcsin 2x$ skall vara definierat måste $-1\le 2x\le 1$, vilket betyder $-1/2\le x\le 1/2$. Detta är alltså definitionsmängden. Värdemängden är densamma som får $\arcsin x$, dvs $\left[-\pi/2,\pi/2\right]$.