Lösningar 5
Matematik för naturvetare 15hp
| Versionen från 27 augusti 2007 kl. 14.41 (redigera) Clas Löfwall (Diskussion | bidrag) (Ny sida: ==Lösningar till några övningar till Lektion 5== Tillbaka till lösningarna) ← Gå till föregående ändring |
Nuvarande version (27 augusti 2007 kl. 14.42) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) |
||
| Rad 1: | Rad 1: | ||
| ==Lösningar till några övningar till Lektion 5== | ==Lösningar till några övningar till Lektion 5== | ||
| [[Exempellösningar | Tillbaka till lösningarna]] | [[Exempellösningar | Tillbaka till lösningarna]] | ||
| + | |||
| + | '''3.1.c)''' | ||
| + | |||
| + | Här får man $y=±1/x$, så till varje värde på $x$ hör ''två'' | ||
| + | värden på $y$. Sambandet uttrycker således inte $y$ som funktion av | ||
| + | $x$. | ||
| + | |||
| + | |||
| + | |||
| + | '''3.1 d)''' | ||
| + | |||
| + | Om vi betraktar $y$ som obekant, så har ekvationen $y^3=x^2+1$ | ||
| + | bara en enda rot, nämligen $y=\root3\of{x^2+1}$. Sambandet uttrycker | ||
| + | därför $y$ som funktion av $x$. | ||
| + | |||
| + | |||
| + | |||
| + | '''3.1 f)''' | ||
| + | |||
| + | Om $x=|y|$, så är $y=±x$, dvs sambandet uttrycker inte $y$ som | ||
| + | funktion av $x$. | ||
| + | |||
| + | |||
| + | '''3.1 i)''' | ||
| + | |||
| + | När $x=0$ kan $y$ vara vad som helst, så sambandet ger inte $y$ som | ||
| + | funktion av $x$. | ||
| + | |||
| + | |||
| + | |||
| + | '''3.4.c)''' | ||
| + | |||
| + | |||
| + | $$f(2-a)=(2-a)-2(2-a)^2=2-a-2(4-4a+a^2)=-2a^2+7a-6$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''3.4 e)''' | ||
| + | |||
| + | <math> | ||
| + | f\left(\frac{1}{2x+1}\right)=\frac{1}{2x+1}-2\cdot\left(\frac{1}{2x+1}\right)^2= | ||
| + | \frac{2x+1-2}{(2x+1)^2}=\frac{2x-1}{(2x+1)^2}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''3.4 f)''' | ||
| + | |||
| + | $$ | ||
| + | f(x+1)-f(x-1)=x+1-2(x+1)^2-(x-1-2(x-1)^2) | ||
| + | =x+1-2x^2-4x-2-x+1+2x^2-4x+2 | ||
| + | =-8x+2$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''3.10.d)''' | ||
| + | |||
| + | Eftersom t ex $f(1)=f(-1)$ så saknas invers. | ||
| + | |||
| + | |||
| + | |||
| + | '''3.10 e)''' | ||
| + | |||
| + | För $x\ge 0$ är $y=x^2$ och för $x<0$ är $y=x(-x)=-x^2$. Rita grafen! Man ser att funktionen är strängt växande, så funktionen har en invers. | ||
| + | För $y\ge 0$ har vi $x=f^{-1}(y)=\sqrt y$. Antag att $y<0$; Då måste $x<0$ eftersom $y\ge0$ för $x\ge0$. Vi har alltså att $y=-x^2$ om $y<0$ och alltså $x^2=-y$ vilket ger att $x=-\sqrt {-y}$ eftersom $x<0$. Sammantaget gäller alltså att $f^{-1}(y)=\sqrt y$ för $y\ge0$ och $f^{-1}(y)=-\sqrt{-y}$ för $y<0$. | ||
Nuvarande version
[redigera] Lösningar till några övningar till Lektion 5
3.1.c)
Här får man $y=±1/x$, så till varje värde på $x$ hör två värden på $y$. Sambandet uttrycker således inte $y$ som funktion av $x$.
3.1 d)
Om vi betraktar $y$ som obekant, så har ekvationen $y^3=x^2+1$ bara en enda rot, nämligen $y=\root3\of{x^2+1}$. Sambandet uttrycker därför $y$ som funktion av $x$.
3.1 f)
Om $x=|y|$, så är $y=±x$, dvs sambandet uttrycker inte $y$ som funktion av $x$.
3.1 i)
När $x=0$ kan $y$ vara vad som helst, så sambandet ger inte $y$ som funktion av $x$.
3.4.c)
$$f(2-a)=(2-a)-2(2-a)^2=2-a-2(4-4a+a^2)=-2a^2+7a-6$$
3.4 e)
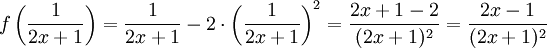
3.4 f)
$$ f(x+1)-f(x-1)=x+1-2(x+1)^2-(x-1-2(x-1)^2) =x+1-2x^2-4x-2-x+1+2x^2-4x+2 =-8x+2$$
3.10.d)
Eftersom t ex $f(1)=f(-1)$ så saknas invers.
3.10 e)
För $x\ge 0$ är $y=x^2$ och för $x<0$ är $y=x(-x)=-x^2$. Rita grafen! Man ser att funktionen är strängt växande, så funktionen har en invers. För $y\ge 0$ har vi $x=f^{-1}(y)=\sqrt y$. Antag att $y<0$; Då måste $x<0$ eftersom $y\ge0$ för $x\ge0$. Vi har alltså att $y=-x^2$ om $y<0$ och alltså $x^2=-y$ vilket ger att $x=-\sqrt {-y}$ eftersom $x<0$. Sammantaget gäller alltså att $f^{-1}(y)=\sqrt y$ för $y\ge0$ och $f^{-1}(y)=-\sqrt{-y}$ för $y<0$.

