Inlämningsuppgift
Matematik för naturvetare 15hp
(Skillnad mellan versioner)
| Versionen från 20 september 2007 kl. 14.40 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 20 september 2007 kl. 14.43 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 11: | Rad 11: | ||
| \begin{vmatrix}1&x&x^2\\1&y&y^2\\1&z&z^2\end{vmatrix}\ne0 | \begin{vmatrix}1&x&x^2\\1&y&y^2\\1&z&z^2\end{vmatrix}\ne0 | ||
| </math> | </math> | ||
| + | |||
| + | |||
| + | ==Uppgift 3== | ||
| + | |||
| + | Lös ekvationssystemet | ||
| + | |||
| + | $\displaystyle{ \left\{ \begin{matrix} \log_x \left( y+\frac{y^2}{4} \right) &=& 3 \\ \log_y ( x^2) &=& 1 \end{matrix} \right. }$ | ||
Versionen från 20 september 2007 kl. 14.43
Uppgift 1
Använd t.ex. de Moivres formel och binomialteoremet för att härleda en formel som uttrycker $\cos5x$ som ett polynom i $\cos x$, eller mer precist bestäm konstanterna $A,B,C$ så att $\cos 5x=A(\cos x)^5+B(\cos x)^3+C\cos x$
Uppgift 2
Låt $x,y,z$ vara tre reella tal som är sinsemellan olika, dvs $x\ne y$ $x\ne z$ $y\ne z$. Visa att
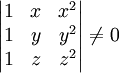
Uppgift 3
Lös ekvationssystemet
$\displaystyle{ \left\{ \begin{matrix} \log_x \left( y+\frac{y^2}{4} \right) &=& 3 \\ \log_y ( x^2) &=& 1 \end{matrix} \right. }$

