Lösningar 13
Matematik för naturvetare 15hp
| Versionen från 2 oktober 2007 kl. 12.57 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 2 oktober 2007 kl. 13.07 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 4: | Rad 4: | ||
| - | 6.1.c) Differenskvoten är \begin{eqnarray*} | + | '''6.1.c)''' |
| + | |||
| + | Differenskvoten är | ||
| + | |||
| + | |||
| + | <math>\begin{array}{ccc} | ||
| \frac{f(x+h)-f(x)}{h}&=&\frac{1}{h}\cdot\left(\frac{1}{x+h}-\frac{1}{x}\right) | \frac{f(x+h)-f(x)}{h}&=&\frac{1}{h}\cdot\left(\frac{1}{x+h}-\frac{1}{x}\right) | ||
| = | = | ||
| \frac{1}{h}\cdot\frac{x-(x+h)}{x(x+h)}\\ | \frac{1}{h}\cdot\frac{x-(x+h)}{x(x+h)}\\ | ||
| &=& | &=& | ||
| - | -\frac{h}{hx(x+h)}=-\frac{1}{x(x+h)}.\end{eqnarray*} | + | -\frac{h}{hx(x+h)}=-\frac{1}{x(x+h)}\end{array}</math> |
| - | Detta ger \[ | + | |
| + | |||
| + | |||
| + | Detta ger | ||
| + | |||
| + | |||
| + | <math> | ||
| f'(x)=\lim_{h\to 0}\left(-\frac{1}{x(x+h)}\right)= | f'(x)=\lim_{h\to 0}\left(-\frac{1}{x(x+h)}\right)= | ||
| - | -\frac{1}{x\cdot x}=-\frac{1}{x^2}.\] | + | -\frac{1}{x\cdot x}=-\frac{1}{x^2}</math> |
| + | |||
| + | |||
| + | |||
| + | '''6.1. d)''' | ||
| + | |||
| + | Differenskvoten är | ||
| - | \vskip 2mm | ||
| - | d) Differenskvoten är \begin{eqnarray*} | + | <math>\begin{array}{ccc} |
| \frac{f(x+h)-f(x)}{h}&=&\frac{\sqrt{x+h}-\sqrt x}{h}= | \frac{f(x+h)-f(x)}{h}&=&\frac{\sqrt{x+h}-\sqrt x}{h}= | ||
| \frac{(\sqrt{x+h}-\sqrt x)(\sqrt{x+h}+\sqrt x)}{h(\sqrt{x+h}+\sqrt | \frac{(\sqrt{x+h}-\sqrt x)(\sqrt{x+h}+\sqrt x)}{h(\sqrt{x+h}+\sqrt | ||
| Rad 22: | Rad 38: | ||
| &=& | &=& | ||
| \frac{(x+h)-x}{h(\sqrt{x+h}+\sqrt x)}=\frac{h}{h(\sqrt{x+h}+\sqrt x)}= | \frac{(x+h)-x}{h(\sqrt{x+h}+\sqrt x)}=\frac{h}{h(\sqrt{x+h}+\sqrt x)}= | ||
| - | \frac{1}{\sqrt{x+h}+\sqrt x}\end{eqnarray*} | + | \frac{1}{\sqrt{x+h}+\sqrt x}\end{array}</math> |
| + | |||
| + | |||
| + | |||
| där vi använde knepet att förlänga med $\sqrt{x+h}+\sqrt x$. Alltså | där vi använde knepet att förlänga med $\sqrt{x+h}+\sqrt x$. Alltså | ||
| - | är \[ | + | är |
| + | |||
| + | |||
| + | <math> | ||
| f'(x)=\lim_{h\to 0}\frac{1}{\sqrt{x+h}+\sqrt x}= | f'(x)=\lim_{h\to 0}\frac{1}{\sqrt{x+h}+\sqrt x}= | ||
| - | \frac{1}{\sqrt x+\sqrt x}=\frac{1}{2\sqrt x}.\] | + | \frac{1}{\sqrt x+\sqrt x}=\frac{1}{2\sqrt x}</math> |
| + | |||
| + | |||
| + | |||
| - | \vskip 2mm | + | '''6.2.d)''' |
| - | 6.2.d) Den här uppgiften är intressant på så sätt att man kan beräkna | + | Den här uppgiften är intressant på så sätt att man kan beräkna |
| derivatan på två olika sätt. Antingen använder man produktregeln på | derivatan på två olika sätt. Antingen använder man produktregeln på | ||
| - | båda termerna: \begin{eqnarray*} | + | båda termerna: |
| + | |||
| + | |||
| + | <math>\begin{array}{ccc} | ||
| f'(x)&=&D(\cos x)\cos x+\cos xD(\cos x)+D(\sin x)\sin x+\sin xD(\sin | f'(x)&=&D(\cos x)\cos x+\cos xD(\cos x)+D(\sin x)\sin x+\sin xD(\sin | ||
| x)\\ | x)\\ | ||
| &=& | &=& | ||
| - | -\sin x\cos x-\sin x\cos x+\cos x\sin x+\cos x\sin x=0\end{eqnarray*} | + | -\sin x\cos x-\sin x\cos x+\cos x\sin x+\cos x\sin x=0\end{array}</math> |
| - | eller så anvnder man först trigonometriska ettan, som ger $f(x)=1$ för | + | |
| - | alla $x$. Alltså är $f'(x)=0$. Det är ju skönt att resultatet blit | + | |
| - | detsamma med de två metoderna! | + | |
| + | eller så använder man först trigonometriska ettan, som ger $f(x)=1$ för | ||
| + | alla $x$. Alltså är $f'(x)=0$. | ||
| + | |||
| + | |||
| - | \vskip 2mm | + | '''6.4.a)''' |
| - | 6.4.a) Lägg först märke till att $\sin x^2$ skall tolkas som | + | Lägg först märke till att $\sin x^2$ skall tolkas som |
| $\sin(x^2)$ och alltså {\it inte} som $(\sin x)^2$! Om vi sätter | $\sin(x^2)$ och alltså {\it inte} som $(\sin x)^2$! Om vi sätter | ||
| $u(v)=\sin v$ och $v(x)=x^2$, så är $f(x)=\sin x^2=u(v(x))$ och enligt | $u(v)=\sin v$ och $v(x)=x^2$, så är $f(x)=\sin x^2=u(v(x))$ och enligt | ||
| - | kedjeregeln är \[ | + | kedjeregeln är |
| - | f'(x)=u'(v(x))v'(x)=\cos v(x)\cdot 2x=2x\cos x^2.\] | + | |
| - | \vskip 2mm | ||
| - | b) Det enklaste sättet att räkna ut derivatan är förstås att | + | <math> |
| + | f'(x)=u'(v(x))v'(x)=\cos v(x)\cdot 2x=2x\cos x^2</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''6.4.b)''' | ||
| + | |||
| + | Det enklaste sättet att räkna ut derivatan är förstås att | ||
| observera att $f(x)=\sin(\arcsin x)=x$, så att $f'(x)=1$. men det går | observera att $f(x)=\sin(\arcsin x)=x$, så att $f'(x)=1$. men det går | ||
| även bra att använda kedjeregeln. Sätt $u(v)=\sin v$ och $v(x)=\arcsin | även bra att använda kedjeregeln. Sätt $u(v)=\sin v$ och $v(x)=\arcsin | ||
| - | x$. Då är \begin{eqnarray*} | + | x$. Då är |
| + | |||
| + | |||
| + | <math>\begin{array}{ccc} | ||
| f'(x)&=&u'(v(x))v'(x)=\cos v(x)\cdot\frac{1}{\sqrt{1-x^2}}= | f'(x)&=&u'(v(x))v'(x)=\cos v(x)\cdot\frac{1}{\sqrt{1-x^2}}= | ||
| \cos(\arcsin x)\cdot\frac{1}{\sqrt{1-x^2}}\\ | \cos(\arcsin x)\cdot\frac{1}{\sqrt{1-x^2}}\\ | ||
| &=& | &=& | ||
| \sqrt{1-\sin^2(\arcsin x)}\cdot\frac{1}{\sqrt{1-x^2}}= | \sqrt{1-\sin^2(\arcsin x)}\cdot\frac{1}{\sqrt{1-x^2}}= | ||
| - | \sqrt{1-x^2}\cdot\frac{1}{\sqrt{1-x^2}}=1.\end{eqnarray*} | + | \sqrt{1-x^2}\cdot\frac{1}{\sqrt{1-x^2}}=1\end{array}</math> |
| + | |||
| + | |||
| + | |||
| (Det andra sättet är ju väsentligen härledningen av derivatan av | (Det andra sättet är ju väsentligen härledningen av derivatan av | ||
| arcussinus.) | arcussinus.) | ||
| - | \vskip 2mm | ||
| - | 6.5.b) Derivatan är \begin{eqnarray*} | + | |
| + | '''6.5.b)''' | ||
| + | |||
| + | Derivatan är | ||
| + | |||
| + | |||
| + | <math>\begin{array}{ccc} | ||
| D\left(\frac{x\ln x}{x^2+1}\right)&=&\frac{D(x\ln x)(x^2+1)-x\ln | D\left(\frac{x\ln x}{x^2+1}\right)&=&\frac{D(x\ln x)(x^2+1)-x\ln | ||
| xD(x^2+1)}{(x^2+1)^2}\\ | xD(x^2+1)}{(x^2+1)^2}\\ | ||
| Rad 71: | Rad 119: | ||
| \frac{(\ln x+x\cdot 1/x)(x^2+1)-x\ln x\cdot 2x}{(x^2+1)^2}\\ | \frac{(\ln x+x\cdot 1/x)(x^2+1)-x\ln x\cdot 2x}{(x^2+1)^2}\\ | ||
| &=& | &=& | ||
| - | \frac{(\ln x+1)(x^2+1)-2x^2\ln x}{(x^2+1)^2}\end{eqnarray*} | + | \frac{(\ln x+1)(x^2+1)-2x^2\ln x}{(x^2+1)^2}\end{array}</math> |
| - | så att \[ | + | |
| - | f'(1)=\frac{(0+1)\cdot (1+1)-2\cdot 0}{(1+1)^2}=\frac{1}{2}.\] | + | |
| - | \vskip 2mm | ||
| - | d) Här måste man använda kedjeregeln. Sätt $u(v)=\ln |v|$ och | + | |
| - | $v(x)=\arctan x$, så att $f(x)=u(v(x))$. Då är \[ | + | så att |
| + | |||
| + | |||
| + | <math> | ||
| + | f'(1)=\frac{(0+1)\cdot (1+1)-2\cdot 0}{(1+1)^2}=\frac{1}{2}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''6.5.d)''' | ||
| + | |||
| + | Här måste man använda kedjeregeln. Sätt $u(v)=\ln |v|$ och | ||
| + | $v(x)=\arctan x$, så att $f(x)=u(v(x))$. Då är | ||
| + | |||
| + | |||
| + | <math> | ||
| f'(x)=u'(v(x))v'(x)=\frac{1}{v(x)}\cdot\frac{1}{1+x^2}= | f'(x)=u'(v(x))v'(x)=\frac{1}{v(x)}\cdot\frac{1}{1+x^2}= | ||
| - | \frac{1}{(1+x^2)\arctan x}.\] | + | \frac{1}{(1+x^2)\arctan x}</math> |
| + | |||
| + | |||
| - | \vskip 2mm | + | '''6.6.b)''' |
| - | 6.6.b) Vi börjar med att förenkla: $\ln|xe^{2x}|=\ln(|x|\cdot | + | Vi börjar med att förenkla: $\ln|xe^{2x}|=\ln(|x|\cdot |
| |e^{2x}|)=\ln |x|+\ln e^{2x}=\ln |x|+2x$ (observera att $e^{2x}>0$ för | |e^{2x}|)=\ln |x|+\ln e^{2x}=\ln |x|+2x$ (observera att $e^{2x}>0$ för | ||
| alla $x$, så vi kan ta bort absolutbeloppstecknen). Derivatan är | alla $x$, så vi kan ta bort absolutbeloppstecknen). Derivatan är | ||
| $1/x+2$ med ett enda nollställe $x=-1/2$. | $1/x+2$ med ett enda nollställe $x=-1/2$. | ||
| - | \vskip 2mm | ||
| - | c) Kvotregeln ger \begin{eqnarray*} | + | |
| + | '''6.6.c)''' | ||
| + | |||
| + | Kvotregeln ger | ||
| + | |||
| + | |||
| + | <math>\begin{array}{ccc} | ||
| D\left(\frac{2x}{1+x^2}\right)&=&\frac{D(2x)(1+x^2)-2xD(1+x^2)}{(1+x^2)^2}= | D\left(\frac{2x}{1+x^2}\right)&=&\frac{D(2x)(1+x^2)-2xD(1+x^2)}{(1+x^2)^2}= | ||
| \frac{2(1+x^2)-2x\cdot 2x}{(1+x^2)^2}\\ | \frac{2(1+x^2)-2x\cdot 2x}{(1+x^2)^2}\\ | ||
| &=& | &=& | ||
| - | \frac{2-2x^2}{(1+x^2)^2}.\end{eqnarray*} | + | \frac{2-2x^2}{(1+x^2)^2}\end{array}</math> |
| + | |||
| + | |||
| + | |||
| Nollställena är således $x=±1$. | Nollställena är således $x=±1$. | ||
| - | \vskip 2mm | ||
| - | d) Sätt $u(v)=\arctan v$ och $v(x)=1-x^2$. Enligt kedjeregeln är derivatan \[ | + | |
| + | '''6.6.d)''' | ||
| + | |||
| + | Sätt $u(v)=\arctan v$ och $v(x)=1-x^2$. Enligt kedjeregeln är derivatan | ||
| + | |||
| + | |||
| + | <math> | ||
| f'(x)=u'(v(x))v'(x)=\frac{1}{1+v(x)^2}\cdot (-2x)= | f'(x)=u'(v(x))v'(x)=\frac{1}{1+v(x)^2}\cdot (-2x)= | ||
| - | \frac{-2x}{1+(1-x^2)^2}.\] | + | \frac{-2x}{1+(1-x^2)^2}</math> |
| + | |||
| + | |||
| + | |||
| Det finns alltså ett enda nollställe, nämligen $x=0$. | Det finns alltså ett enda nollställe, nämligen $x=0$. | ||
| - | \vskip 2mm | ||
| - | 6.7. Vi börjar med att fundera över hur vinkeln mellan en linje | + | |
| + | '''6.7.''' | ||
| + | |||
| + | Vi börjar med att fundera över hur vinkeln mellan en linje | ||
| $y=kx+m$ och $x$-axeln beror på konstanterna $k$ och $m$. Om $k=0$ så | $y=kx+m$ och $x$-axeln beror på konstanterna $k$ och $m$. Om $k=0$ så | ||
| är linjen parallell med $x$-axeln och i så fall skär de varandra bara | är linjen parallell med $x$-axeln och i så fall skär de varandra bara | ||
| Rad 116: | Rad 195: | ||
| =k/1=k$. | =k/1=k$. | ||
| - | \vskip 2mm | + | |
| \begin{center}\includegraphics{Fig1dag13.jpg}\end{center} | \begin{center}\includegraphics{Fig1dag13.jpg}\end{center} | ||
Versionen från 2 oktober 2007 kl. 13.07
Lösningar till några övningar till lektion 12
6.1.c)
Differenskvoten är
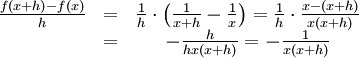
Detta ger
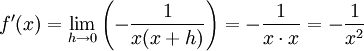
6.1. d)
Differenskvoten är
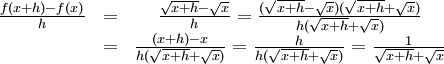
där vi använde knepet att förlänga med $\sqrt{x+h}+\sqrt x$. Alltså är
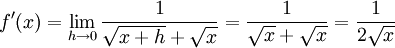
6.2.d)
Den här uppgiften är intressant på så sätt att man kan beräkna derivatan på två olika sätt. Antingen använder man produktregeln på båda termerna:
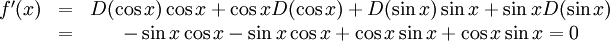
eller så använder man först trigonometriska ettan, som ger $f(x)=1$ för alla $x$. Alltså är $f'(x)=0$.
6.4.a)
Lägg först märke till att $\sin x^2$ skall tolkas som $\sin(x^2)$ och alltså {\it inte} som $(\sin x)^2$! Om vi sätter $u(v)=\sin v$ och $v(x)=x^2$, så är $f(x)=\sin x^2=u(v(x))$ och enligt kedjeregeln är
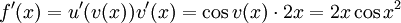
6.4.b)
Det enklaste sättet att räkna ut derivatan är förstås att observera att $f(x)=\sin(\arcsin x)=x$, så att $f'(x)=1$. men det går även bra att använda kedjeregeln. Sätt $u(v)=\sin v$ och $v(x)=\arcsin x$. Då är
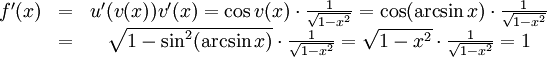
(Det andra sättet är ju väsentligen härledningen av derivatan av arcussinus.)
6.5.b)
Derivatan är
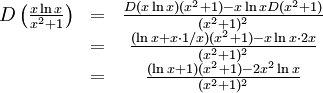
så att
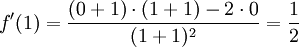
6.5.d)
Här måste man använda kedjeregeln. Sätt $u(v)=\ln |v|$ och $v(x)=\arctan x$, så att $f(x)=u(v(x))$. Då är

6.6.b)
Vi börjar med att förenkla: $\ln|xe^{2x}|=\ln(|x|\cdot |e^{2x}|)=\ln |x|+\ln e^{2x}=\ln |x|+2x$ (observera att $e^{2x}>0$ för alla $x$, så vi kan ta bort absolutbeloppstecknen). Derivatan är $1/x+2$ med ett enda nollställe $x=-1/2$.
6.6.c)
Kvotregeln ger
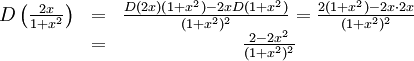
Nollställena är således $x=±1$.
6.6.d)
Sätt $u(v)=\arctan v$ och $v(x)=1-x^2$. Enligt kedjeregeln är derivatan
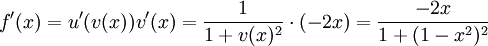
Det finns alltså ett enda nollställe, nämligen $x=0$.
6.7.
Vi börjar med att fundera över hur vinkeln mellan en linje $y=kx+m$ och $x$-axeln beror på konstanterna $k$ och $m$. Om $k=0$ så är linjen parallell med $x$-axeln och i så fall skär de varandra bara i fallet $m=0$ (i vilket fall de sammanfaller). Vinkeln är då 0. Antag att $k\not=0$ och beteckna skärningspunkten med $(a,0)$. Om $x$-koordinaten ökar med 1, så ökar $y$-koordinaten med $k$ (vilket är en minskning om $k<0$). I figuren nedan ser vi att $\tan\alpha =k/1=k$.
\begin{center}\includegraphics{Fig1dag13.jpg}\end{center}
\vskip 2mm
Riktningskoefficienten $k$ är lika med derivatan av $f$ för $x=2$, som är \[ f'(2)=3\cdot 3\cdot 2^2-3\cdot 2\cdot 2-25=-1.\] Vinkeln mellan tangenten och positiva $x$-axeln är således $3¹/4$, så den spetsiga vinkeln är $¹/4$.
\vskip 2mm
6.9. Enligt kedjeregeln är \[ f'(x)=\frac{1}{1+(x^2-4)^2}\cdot 2x,\quad\mbox{varför}\quad f'(2)=\frac{2\cdot 2}{1+0^2}=4.\] Eftersom $f(2)=\arctan(2^2-4)=0$ så är tangentens ekvation $y-0=4(x-2)$, dvs $y=4x-8$.
\vskip 2mm
6.11. Mellan kl 6 på morgonen och kl 6 på eftermiddagen har temperaturen ändrats med \begin{eqnarray*} T(18)-T(6)&=&12+6\sin\frac{¹(18-8)}{12}-12-6\sin\frac{¹(6-8)}{12}\\ &=& 6\sin\frac{5¹}{6}-6\sin\left(-\frac{¹}{6}\right)=3+3=6.\end{eqnarray*} Medeländringen är \[ \frac{T(18)-T(6)}{18-6}=\frac{6}{12}=\frac{1}{2}.\] Derivatan är \[ T'(t)=6\cdot\frac{¹}{12}\cos\left(\frac{¹(t-8)}{12}\right)= \frac{¹}{2}\cos\left(\frac{¹(t-8)}{12}\right).\] Förändringshastigheten kl 4 på morgonen är \[ T'(4)=\frac{¹}{2}\cos\left(\frac{¹(4-8)}{12}\right)= \frac{¹}{2}\cos\left(-\frac{¹}{3}\right)=\frac{¹}{4}.\] På samma sätt räknar man ut förändringshastigheten kl 8 på fm och 4 på em. Den är 0 då $¹(t-8)/12=±¹/2$, vilket ger $t=2$ eller $t=14$, dvs kl 2 på fm och em. Enheten är i alla fallen grader per timme.

