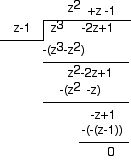Lösningar 6

Matematik för naturvetare 15hp

---

Versionen från 24 augusti 2007 kl. 16.26

[redigera] Lösningar till några övningar till Lektion 6

Tillbaka till lösningarna

4.1-3

Att bestämma nollställena till ett polynom $p(x)$ är ju detsamma som att lösa ekvationen $p(x)=0$ och max/minpunkter kan vi hitta med kvadratkomplettering.

a) Kvadratkomplettering ger

$\begin{array} p(x)&=&x^2+3x-4\\ &=&\left(x+\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2-4\\ &=&\left(x+\frac{3}{2}\right)^2-\frac{25}{4}. \end{array}$

Ekvationen $p(x)=0$ är alltså ekvivalent med

$\left(x+\frac{3}{2}\right)^2=\frac{25}{4},$

som ger

$x+\frac{3}{2}=±\frac{5}{2}\quad\mbox{och alltså}\quad x=-\frac{3}{2}±\frac{5}{2}.$

Rštterna är $x_{1}=-4$ och $x_{2}=1$. Enligt faktorsatsen är $p(x)$ delbart med $x-(-4)=x+4$ och $x-1$ och mycket riktigt är $p(x)=x^2+3x-4=(x+4)(x-1)$. Det minsta värde som $p$ kan anta är $-25/4$ eftersom $\left(x+\frac{3}{2}\right)^2\ge 0$ för alla $x$ och värdet $-25/4$ antas verkligen för $x=-3/2$.

b) Här får vi

$\begin{array} p(x)&=& 3x-1-2x^2=(-2)\left(x^2-\frac{3}{2}\, x+\frac{1}{2}\right) \\ &=& (-2)\left(\left(x-\frac{3}{4}\right)^2-\left(\frac{3}{4}\right)^2 +\frac{1}{2}\right)\\ &=&\frac{1}{8}-2\left(x-\frac{3}{4}\right)^2. \end{array}$

Ekvationen $p(x)=0$ kan skrivas $(x-3/4)^2=1/16$ som ger $x=3/4±1/4$. Rötterna är $x_{1}=1/2$ och $x_{2}=1$. Enligt faktorsatsen är $p(x)$ delbart med $x-1/2$ och $x-1$ och vi har

$p(x)=(-2)(x-1/2)(x-1)=(-2x+1)(x-1).$

Här har $p$ inget minsta värde, men väl ett största, nämligen $1/8$ som antas för $x=3/4$.

4.7.a)

4.8.a) Sätter vi $t=x^2$ så får vi ekvationen $2t^2-t-6=0$ eller $t^2-t/2-3=0$. Rötterna till denna är

$t=\frac{1}{4}±\sqrt{\frac{1}{16}+3}=\frac{1}{4}±\frac{7}{4},$

dvs $t_{1}=-6/4=-3/2$, $t_{2}=2$. För att lösa den ursprungliga ekvationen måste vi lösa $x^2=t_{1}$ och $x^2=2$. Här har $x^2=-3/2$ inga reella lösningar och $x^2=2$ ger $x=±\sqrt 2$.

b) Sätter vi $t=x^3$ så får vi $t^2-t-2=0$ med rötterna $t_{1}=-1$, $t_{2}=2$. Ekvationerna $x^3=-1$ och $x^3=2$ har rötterna $-1$ och $\root3\of 2$, som alltså är den givna ekvationens rötter.

4.9. Placera ett koordinatsystem så att origo ligger i markplanet och bergets topp på $y$-axeln där $y=24$. Kastparabeln har en ekvation av formen $p(x)=ax^2+bx+c$. Vi har $p(0)=24$, så $c=24$. Kvadratkomplettering ger $p(x)=a(x+b/2a)^2+24-b^2/4a$. Här måste $a<0$ eftersom $p$ har ett största värde. Detta antas för $x=5$, varför $b/2a=-5$. Värdet är 49, så $24-b^2/4a=49$. Detta ger $b^2/4a=-25$. Dividerar vi detta med $b/2a=-5$ så får vi $b=10$ och därefter $a=-1$. Parabelns ekvation är således $p(x)=-x^2+10x+24$. Kvadratkompletteringen har vi redan gjort, nämligen $p(x)=49-(x-5)^2$ och det återstår att lösa ekvationen $p(x)=0$. Vi får $x-5=±7$ och $x=-2$ eller $x=12$. Svaret är således att bollen faller i backen 12 meter från bergstoppen längs marken.

Bild:Fig2dag8

4.11.d) $4\cdot 10^x=e^{\ln 4}\cdot (e^{\ln 10})^x= e^{x\ln 10+\ln 4}$

4.14. Ett bekvämt sätt att lösa den här uppgiften är att översätta 8-logaritmer till 2-logaritmer, vilket är enkelt eftersom 8 är en potens av 2, $8=2^3$. Sätt $a=\log_{8}t$, så att $t=8^a$. Då är $t=(2^3)^a=2^{3a}$, så att $\log_{2}t=3a=3\log_{8} t$. Uppgiften går alltså ut på att bestämma $3\log_{2}x^2=6\log_{2}x$ för vissa värden på $x$.

4.15. Vi skall lösa ekvationen $\log_{25}(x+2)=\log_{5}x$ och får

$x+2=25^{\log_{25}(x+2)}=25^{\log_{5}x}=(5^2)^{\log_{5}x}=(5^{\log_{5}x})^2=x^2.$

Andragradsekvationen $x^2=x+2$ har två rötter, $x=-1$ och $x=2$. Bara den senare duger (varför?), så svaret är $x=2$.

4.18.b) Vi har $\sin a=\sin b$ om och endast om $a=b+2n^\pi$ eller $a=¹-b+2n¹$. Alltså $3v=2v+2n\pi$ eller $3v=¹-2v+2n¹$, dvs $v=2n\pi$ eller $v=\pi/5+2n¹/5$ för $n\in{\bf Z}$.

c) Använd att $\cos u=\sin (\pi/2-u)$ och fortsätt som i a).

e) Ekvationen kan skrivas som $\cos v(\sin v-1)=0$, $\sin v\not=0$. Då måste antingen $\cos v=0$ eller $\sin v-1=0$.