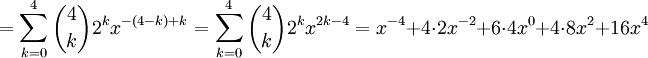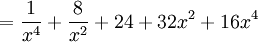Lösningar 4
Matematik för naturvetare 15hp
[redigera] Lösningar till några övningar till Lektion 4
2.2.d)
Ledning: Talen 2, 4, 16 och 256 osv är potenser av 2.
2.5
Beteckna radien från början med $R_{0}$ och radien efter 42 dagar med $R$. Motsvarande volymer är $V_{0}=4\pi R_{0}^3/3$ respektive $V=4\pi R^3/3$. 42 dagar är 3 14-dagarsperioder, så $V=2\cdot 2\cdot 2\cdot V_{0}=8V_{0}$. Härav får vi $R^3=8R_{0}^3$ och $R=2R_{0}$.
2.9
Om det $n$:te talet är $a_{n}$ och kvoten $k$, så gäller $a_{n}=a_{1}k^{n-1}$. Alltså är $a_{3}=a_{1}k^2$, vilket ger $7=a_{1}(-1/2)^2$ och $a_{1}=28$. Det sjätte talet blir $a_{6}=28(-1/2)^5=-7/8$.
2.12
Låt organismens vikt från början vara $m$. Efter en matning väger den
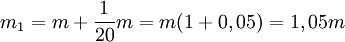
och efter två matningar (dvs efter en timme)
m2 = m1 + 0,05m1 = 1,052m
osv, så att efter n matningar (och alltså n-1 timmar) $$ m_{n}=1,05^nm$$ För att få reda på när den har fördubblat sin vikt måste vi lösa ekvationen $1,05^n=2$, som ger $n=\ln 2/\ln 1,05\approx 14,2$. Svaret är alltså efter 15:e matningen, dvs efter 14 timmar (i facit står det 15 timmar).
2.19 b)
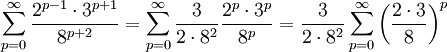
Detta är en geometrisk serie med första term 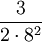 och kvot $(2\cdot 3)/8=3/4$. Eftersom
kvoten ligger mellan $-1$ och 1 så är serien konvergent och dess
summa är
och kvot $(2\cdot 3)/8=3/4$. Eftersom
kvoten ligger mellan $-1$ och 1 så är serien konvergent och dess
summa är
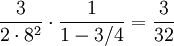
2.19 d)
Som den står är serien inte geometrisk, men man kan dela upp den i två geometriska serier:

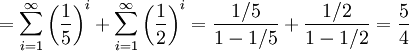
Observera att seriernas kvoter $1/5$ och $1/2$ ligger mellan $-1$ och 1 så att serierna är konvergenta.
2.19 e)
Sätt $k=t+2$:
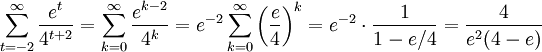
eftersom kvoten $e/4$ ligger mellan $-1$ och 1.
2.19 f)
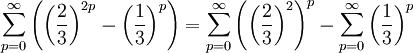
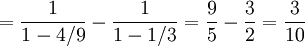
eftersom kvoterna $4/9$ och $1/3$ ligger mellan $-1$ och 1.
2.32.c)
Binomialsatsen ger