Lösningar 8

Matematik för naturvetare 15hp

Hoppa till: navigering, sök

[redigera] Lösningar till några övningar till lektion 8

Tillbaka till lösningarna


1.44.a)

Kvadratkomplettering ger $(z+2)^2+1=0$, varav $(z+2)^2=-1$ och $z+2=±i$ (undvik att skriva $±\sqrt{-1}$). Rötterna är $z=-2±i$.


1.44.b)

Kvadratkomplettering ger $(z-3)^2+4=0$, varav $(z-3)^2=-4$ och $z-3=±2i$. Rötterna är $z=3±2i$.


1.45.c)

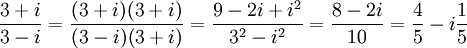
\frac{3+i}{3-i}=\frac{(3+i)(3+i)}{(3-i)(3+i)}=\frac{9-2i+i^2}{3^2-i^2}=\frac{8-2i}{10}=\frac{4}{5}-i\frac{1}{5}


1.45 d)

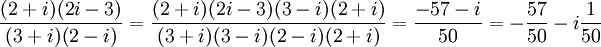
\frac{(2+i)(2i-3)}{(3+i)(2-i)}=\frac{(2+i)(2i-3)(3-i)(2+i)}{(3+i)(3-i) (2-i)(2+i)}=\frac{-57-i}{50}=-\frac{57}{50}-i\frac{1}{50}


1.46.a)

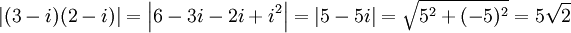
\left|(3-i)(2-i)\right|=\left|6-3i-2i+i^2\right|= \left|5-5i\right|=\sqrt{5^2+(-5)^2}=5\sqrt 2


1.46 b)

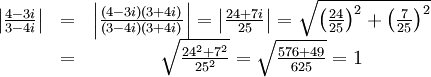
\begin{matrix} \left|\frac{4-3i}{3-4i}\right|&=&\left|\frac{(4-3i)(3+4i)}{(3-4i)(3+4i)}\right|= \left|\frac{24+7i}{25}\right|=\sqrt{\left(\frac{24}{25}\right)^2+ \left(\frac{7}{25}\right)^2}\\ &=&\sqrt{\frac{24^2+7^2}{25^2}}=\sqrt{\frac{576+49}{625}}=1\end{matrix}


Observera att talet kunde lösas enklare genom att utnyttja resultatet i övning 1.47 d). Det gäller nämligen att

| 4 − 3i | = | 3 − 4i |


13.21.a

Sätt $z=2-2i$. Då är $|z|=\sqrt{2^2+(-2)^2}=2\sqrt 2$. I figuren nedan ser man att argumentet är $-\pi/4$ eller $2\pi{}-\pi{}/4=7\pi{}/4$, så $z=2\sqrt 2(\cos(-\pi{}/4)+i\sin(-\pi{}/4))$.


13.21 b

Sätt $z=-1+i\sqrt 3$. Då är $|z|=\sqrt{(-1)^2+(\sqrt 3)^3}=\sqrt 4=2$. Med $u$ som i figuren är $\sin u=\sqrt 3/2$, så $u=\pi{}/3$ och $\arg z=2\pi{}/3$. Alltså är $z=2(\cos (2\pi{}/3)+i\sin(2\pi{}/3))$.


13.21 c

Sätt $z=\sqrt 2+i\sqrt 6$. Då är $|z|=\sqrt{(\sqrt 2)^2+(\sqrt 6)^2}=\sqrt 8=2\sqrt 2$. Med $v$ som i figuren (dvs $v=\arg z$) är $\sin v=\sqrt 6/2\sqrt 2=\sqrt 3/2$, dvs $\arg z=\pi{}/3$. Alltså är $z=2\sqrt 2(\cos(\pi{}/3)+i\sin(\pi{}/3))$.

Bild: Fig1dag22.jpg


13.22 a

Av $|i|=1$ och $\arg i=\pi{}/2$ följer $i=e^{i\pi{}/2}$.


13.22 b

$|-3|=3$ och $\arg (-3)=\pi{}$ ger $-3=3e^{i\pi{}}$.


13.22 c

$|-1-i|=\sqrt 2$ och $\arg(-1-i)=5\pi{}/4$ (rita figur!) ger $-1-i=\sqrt 2 e^{5\pi{}i/4}$.


13.22 d

$|-2i|=2$ och $\arg(-2i)=3\pi{}/2$ ger $-2i=2e^{3\pi{}i/2}$.


13.23

Bestäm först absolutbelopp och argument av $z_1$ och $z_2$:

$$ |z_1|=\sqrt{2^2+2^2}=2\sqrt 2, \quad |z_2|=\sqrt{(\sqrt 3)^2+(-1)^2}=2.$$

Vi har $\arg z_1=\pi{}/4$ (talet ligger ju på bisektrisen mellan axlarna, dvs linjen $\mathrm{Re}\, (z)=\mathrm{Im}\, (z)$). Låt $u$ vara vinkeln mellan positiva reella axeln och linjen mellan 0 och $z_2$. Då är $\sin u=1/2$, så $u=\pi{}/6$. Alltså kan vi ta $\arg z_2=-\pi{}/6$.


13.23 a

$|z_1\cdot z_2|=|z_1|\cdot |z_2|=4\sqrt 2$, $\arg(z_1\cdot z_2)=\arg z_1+\arg z_2=\pi{}/4-\pi{}/6=\pi{}/12$


13.23 b

$|\bar z_1\cdot z_2|=|\bar z_1|\cdot |z_2|=|z_1|\cdot |z_2|=4\sqrt 2$, $\arg(\bar z_1\cdot z_2)= \arg(\bar z_1)+\arg z_2=-\arg z_1+\arg z_2=-\pi{}/4-\pi{}/6=-5\pi{}/12$.


13.23 c

$|z_1/z_2|=|z_1|/|z_2|=\sqrt 2$, $\arg(z_1/z_2)=\arg z_1-\arg z_2=\pi{}/4+\pi{}/6=5\pi{}/12$


13.23 d

$|z_1^3|=|z_1|^3=(2\sqrt 2)^3=16\sqrt 2$, $\arg z_1^3=3\arg z_1=3\pi{}/4$


13.23 e

$|z_2^2/z_1|=|z_2|^2/|z_1|=2^2/2\sqrt 2=\sqrt 2$, $\arg(z_2^2/z_1)=2\arg z_2-\arg z_1=-2\pi{}/6-\pi{}/4=-7\pi{}/12$

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/L%C3%B6sningar_8
Personliga verktyg