1.1 Inledning till derivata

Sommarmatte 2

(Skillnad mellan versioner)

Hoppa till: navigering, sök

Nuvarande version

Innehåll:

Derivatans definition (översiktligt).
Derivatan av $\,x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x$.
Derivata av summa och differens.
Tangent och normal till kurvor.

Lärandemål:
Efter detta avsnitt ska du ha lärt dig att:

Förstå derivatan $\,f^{\,\prime}(a)\,$ som lutningen av kurvan $\,y=f(x)\,$ i punkten $\,x=a\,$.
Förstå derivatan som den momentana ändringstakten av en storhet (exempelvis fart, prisökning, o.s.v.).
Veta att det finns funktioner som inte är deriverbara (t.ex. $\,f(x)=\vert x\vert\,$ i $\,x=0\,$).
Kunna derivera $x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x\,$ samt summor/differenser av sådana termer.
Kunna bestämma tangent och normal till $y=f(x)$.
Veta att derivatan kan betecknas med $\,f^{\,\prime}(x)\,$ och $\,df/dx(x)\,$.

Övningar

[redigera] Inledning

När man studerar matematiska funktioner och deras grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.

Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde ($\,y\,$) ändras för varje enhets ökning av variabelvärdet ($\,x\,$). Om man känner till två punkter på en funktions graf kan man få ett mått på funktionens förändringsgrad mellan dessa punkter genom att beräkna ändringskvoten

$$\frac{\Delta y}{\Delta x}= \frac{\text{skillnad i y-led}}{\text{skillnad i x-led}}$$

Exempel 1

De linjära funktionerna $\,f(x)=x\,$ respektive $\,g(x)=-2x\,$ förändras på samma sätt hela tiden. Deras förändringsgrad är $\,1\,$ resp. $\,−2\,$, vilket vi känner till som linjernas respektive riktningskoefficient.

För en linjär funktion gäller alltså att funktionens förändringsgrad är samma som linjens riktningskoefficient.

Om man har en funktion där funktionsvärdet förändras med tiden är det naturligt att använda begreppet förändringshastighet, eftersom förändringsgraden här anger hur funktionsvärdet ändras per tidsenhet.

Om en bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, s km, efter t timmar beskrivas med funktionen $\,s(t)=80 t\,$. Funktionens förändringsgrad anger hur funktionsvärdet ändras per timme, vilket naturligtvis är detsamma som bilens hastighet, 80 km/h.

För icke-linjära funktioner gäller ju att lutningen på funktionskurvan ändras hela tiden och därmed också funktionens förändringsgrad. För att bestämma hur en sådan funktion förändras kan vi antingen ange funktionens genomsnittliga förändring (medelförändringen) mellan två punkter på funktionskurvan, eller den momentana förändringsgraden i en punkt på kurvan.

Exempel 2

För funktionen $\,f(x)=4x-x^2\,$ är $\,f(1)=3\,$, $\,f(2)=4\,$ och $\,f(4)=0\,$.

Medelförändringen (medellutningen) från $\,x = 1\,$ till $\,x = 2\,$ är $$\frac{\Delta y}{\Delta x}= \frac{f(2)-f(1)}{2-1} = \frac{4-3}{1}=1\,\mbox{,}$$ och funktionen ökar i detta intervall.
Medelförändringen från $\,x = 2\,$ till $\,x = 4\,$ är $$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(2)}{4-2}= \frac{0-4}{2}=-2\,\mbox{,}$$ och funktionen avtar i detta intervall.
Mellan $\,x = 1\,$ och $\,x = 4\,$ är medelförändringen $$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(1)}{4-1}= \frac{0-3}{3}=-1\,\mbox{.}$$ I genomsnitt är funktionen avtagande i detta intervall, även om funktionen både växer och avtar i intervallet.

[redigera] Derivatans definition

För att beräkna den momentana förändringsgraden hos en funktion, dvs. funktionskurvans lutning i en punkt $\,P\,$, tar vi temporärt hjälp av ytterligare en punkt $\,Q\,$ i närheten av $\,P\,$ och bildar ändringskvoten mellan $\,P\,$ och $\,Q\,$:

Ändringskvoten $$\frac{\Delta y}{\Delta x}= \frac{f(x+h)-f(x)}{(x+h)-x}= \frac{f(x+h)-f(x)}{h}$$

Om vi låter $\,Q\,$ närma sig $\,P\,$ (dvs. låter $\,h \rightarrow 0\,$) så kan vi lista ut vad värdet blir om punkterna sammanfaller och därmed få fram lutningen i punkten $\,P\,$. Vi kallar detta värde för derivatan av $\,f(x)\,$ i punkten $\,P\,$, vilket kan tolkas som den momentana förändringsgraden av $\,f(x)\,$ i punkten $\,P\,$.

Derivatan av en funktion $\,f(x)\,$ betecknas $\,f^{\,\prime}(x)\,$ och kan formellt definieras så här:

Derivatan av en funktion $\,f(x)\,$, definieras som $$f^{\,\prime}(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \,.$$ Om $\,f^{\,\prime}(x_0)\,$ existerar, säger man att $\,f(x)\,$ är deriverbar i punkten $\,x=x_0\,$.

Olika symboler för derivatan förekommer, t.ex.

Funktion	Derivata
$f(x)$	$f^{\,\prime}(x)$
$y$	$y^{\,\prime}$
$y$	$Dy$
$y$	$\displaystyle\frac{dy}{dx}$
$s(t)$	$\dot s(t)$

[redigera] Derivatans tecken

Derivatans tecken (+/−) visar oss om funktionens graf lutar uppåt eller nedåt, dvs. om funktionen är växande eller avtagande:

$f^{\,\prime}(x)>0\,$ (positiv lutning) medför att $\,f(x)\,$ är växande.
$f^{\,\prime}(x)<0\,$ (negativ lutning) medför att $\,f(x)\,$ är avtagande.
$f^{\,\prime}(x)=0\,$ (ingen lutning) medför att $\,f(x)\,$ är stationär (horisontell).

Exempel 3

$f(2)=3\ $ betyder att funktionens värde är $\,3\,$ när $\,x=2\,$.
$f^{\,\prime}(2)=3\ $ betyder att derivatans värde är $\,3\,$ när $\,x=2\,$, vilket i sin tur betyder att funktionens graf har lutningen $\,3\,$ när $\,x=2\,$.

Exempel 4

I figuren kan man utläsa att

$\displaystyle\eqalign{f^{\,\prime}(a) &> 0\cr f(b) &= 0\cr f^{\,\prime}(c) &= 0\cr f(d) &= 0\cr f^{\,\prime}(e) &= 0\cr f(e) &< 0\cr f^{\,\prime}(g) &> 0} $

Notera betydelsen av $\,f(x)\,$ respektive $\,f^{\,\prime}(x)\,$.

Exempel 5

Temperaturen i en termos beskrivs av en funktion, där $\,T(t)\,$ är temperaturen i termosen efter $\,t\,$ minuter. Skriv följande med matematiska symboler:

Efter 10 minuter är temperaturen 80°.

$T(10)=80$
Efter 2 minuter sjunker temperaturen i termosen med 3° per minut.

$T'(2)=-3\,$ (funktionen är avtagande, varför derivatan är negativ)

Exempel 6

Funktionen $\,f(x)=|x|\,$ saknar derivata då $\,x=0\,$. Man kan nämligen inte bestämma hur funktionens graf lutar i punkten $\,(0,0)\,$ (se figuren nedan).

Man kan uttrycka detta på exempelvis något av följande sätt: "$\,f^{\,\prime}(0)\,$ existerar inte" , "$\,f^{\,\prime}(0)\,$ är ej definerad" eller "$\,f(x)\,$ är inte deriverbar i $\,x=0\,$".

[redigera] Deriveringsregler

Med hjälp av derivatans definition kan man bestämma derivatan för de vanliga funktionstyperna.

Exempel 7

Om $\,f(x)=x^2\,$ så får vi enligt definitionen av derivata ändringskvoten

$$\frac{(x+h)^2-x^2}{h}=\frac{x^2+2hx+h^2-x^2}{h} = \frac{h(2x+h)}{h} = 2x + h\,\mbox{.}$$

Om vi sedan låter $\,h\,$ gå mot noll så ser vi att lutningen i punkten blir $\,2x\,$. Vi har därmed visat att lutningen i en godtycklig punkt på kurvan $\,y=x^2\,$ är $\,2x\,$, dvs. derivatan av $\,x^2\,$ är $\,2x\,$.

På liknande sätt kan man härleda allmänna deriveringsregler:

Funktion	Derivata
$x^n$	$n \cdot x^{n-1}$
$\ln x$	$1/x$
$e^x$	$e^x$
$\sin x$	$\cos x$
$\cos x$	$-\sin x$
$\tan x$	$1/\cos^2 x$

Dessutom gäller för summor och differenser av funktionsuttryck att $$D(f(x) +g(x))= f^{\,\prime}(x) + g'(x)\,\mbox{.}$$

Samt, om k är en konstant, att $$D(k \cdot f(x)) = k \cdot f^{\,\prime}(x)\,\mbox{.}$$

Exempel 8

$D(2x^3 - 4x + 10 - \sin x) = 6x^2 - 4 + 0 - \cos x\,$.
$ y= 3 \ln x + 2e^x \quad$ ger att $\quad\displaystyle y'= 3 \cdot\frac{1}{x} + 2 e^x = \frac{3}{x} + 2 e^x\,$.
$\displaystyle \frac{d}{dx}\Bigl(\frac{3x^2}{5} - \frac{x^3}{2}\Bigr) = \frac{d}{dx}\bigl({\textstyle\frac{3}{5}}x^2 - {\textstyle\frac{1}{2}}x^3\bigr)= {\textstyle\frac{3}{5}}\cdot 2x - {\textstyle\frac{1}{2}}\cdot 3x^2= {\textstyle\frac{6}{5}}x - {\textstyle\frac{3}{2}}x^2\,$.
$\displaystyle s(t)= v_0t + \frac{at^2}{2} \quad$ ger att $\quad\displaystyle s'(t)=v_0 + \frac{2at}{2} = v_0 + at\,$.

Exempel 9

$\displaystyle f(x) = \frac{1}{x} = x^{-1} \quad$ ger att $\quad\displaystyle f^{\,\prime}(x) = -1 \cdot x^{-2} = -\frac{1}{x^2}\,$.
$\displaystyle f(x)= \frac{1}{3x^2} = {\textstyle\frac{1}{3}}\cdot x^{-2} \quad$ ger att $\quad\displaystyle f^{\,\prime}(x) = {\textstyle\frac{1}{3}}\cdot(-2)x^{-3} = -\frac{2}{3} \cdot x^{-3} = -\frac{2}{3x^3}\,$.
$\displaystyle g(t) = \frac{t^2 - 2t + 1}{t} = t -2 + \frac{1}{t} \quad$ ger att $\quad\displaystyle g'(t) = 1 - \frac{1}{t^2}\,$.
$\displaystyle y = \Bigl( x^2 + \frac{1}{x} \Bigr)^2 = (x^2)^2 + 2 \cdot x^2 \cdot \frac{1}{x} + \Bigl(\frac{1}{x} \Bigr)^2 = x^4 + 2x + x^{-2}$
$\qquad\quad$ ger att $\quad\displaystyle y' =4x^3 + 2 -2x^{-3} = 4x^3 + 2 - \frac{2}{x^3}\,$.

Exempel 10

Funktionen $\,f(x)=x^2 + x^{-2}\,$ har derivatan $$f^{\,\prime}(x) = 2x^1 -2x^{-3} = 2x - \frac{2}{x^3}\,\mbox{.}$$ Detta betyder exempelvis att $\,f^{\,\prime}(2) = 2\cdot 2 - 2/2^3= 4- \frac{1}{4} = \frac{15}{4}\,$ och att $\,f^{\,\prime}(-1) = 2 \cdot (-1) - 2/(-1)^3 = -2 + 2 = 0\,$. Däremot är derivatan $\,f'(0)\,$ inte definierad.

Exempel 11

Ett föremål rör sig enligt $\,s(t) = t^3 -4t^2 +5t\,$, där $\,s(t)\,$ km är avståndet från startpunkten efter $\,t\,$ timmar. Beräkna $\,s'(3)\,$ och förklara vad värdet står för.

Tidsderivatan ges av $$s'(t) = 3t^2 - 8t +5\qquad\text{vilket ger att}\qquad s'(3) = 3 \cdot 3^2 - 8 \cdot 3 + 5 = 8\,\mbox{.}$$ Detta kan tolkas som att efter 3 timmar är föremålets hastighet 8 km/h.

Exempel 12

Totalkostnaden $\,T\,$ kr för tillverkning av $\,x\,$ gummidräkter ges av funktionen $$ T(x) = 40000 + 370x -0{,}09x^2 \quad \text{för} \ 0 \le x \le 200\,\mbox{.}$$ Beräkna och förklara innebörden av nedanstående uttryck.

$T(120)$

$T(120)=40000 + 370 \cdot 120 - 0{,}09 \cdot 120^2 = 83104\,$.
Totalkostnaden för att tillverka 120 gummidräkter är 83104 kr.
$T'(120)$

Derivatan ges av $\,T^{\,\prime}(x)= 370 - 0{,}18x\,$ och därför är $\,T^{\,\prime}(120) = 370 - 0{,}18 \cdot 120 \approx 348\,$.
Marginalkostnaden ("kostnaden för att tillverka ytterligare 1 enhet") vid 120 tillverkade gummidräkter är approximativt 348 kr.

[redigera] Tangenter och normaler

En tangent till en kurva är en rät linje som tangerar kurvan.

En normal till en kurva är en rät linje som är vinkelrät mot kurvan i en viss punkt på kurvan (och därmed också vinkelrät mot kurvans tangent i denna punkt).

För vinkelräta linjer gäller att produkten av deras riktningskoefficienter är $\,–1\,$, dvs. om tangentens riktningskoefficient betecknas $\,k_T\,$ och normalens $\,k_N\,$ så är $\,k_T \cdot k_N = -1\,$. Eftersom vi kan bestämma lutningen på en kurva med hjälp av derivatan så kan vi också bestämma ekvationen för en tangent eller en normal om vi känner till funktionsuttrycket för kurvan.

Exempel 13

Bestäm ekvationen för tangenten respektive normalen till kurvan $\,y=x^2 + 1\,$ i punkten $\,(1,2)\,$.

Vi skriver tangentens ekvation som $\,y = kx + m\,$. Eftersom den ska tangera kurvan i $\,x=1\,$ har vi att $\,k= y'(1)\,$, dvs.

$\qquad y' = 2x\,,\qquad y'(1) = 2\cdot 1 = 2\,$.

Tangentlinjen ska också passerar genom punkten $\,(1,2)\,$ och därför måste $\,(1,2)\,$ uppfylla tangentens ekvation

$\qquad 2 = 2 \cdot 1 + m \quad \Leftrightarrow \quad m = 0\,$.

Tangentens ekvation är alltså $\,y=2x\,$.

Riktningskoefficienten för normalen är $\displaystyle k_N = -\frac{1}{k_T} = -\frac{1}{2}$ .

Vidare går normalen också genom punkten $\,(1, 2)\,$ , dvs.

$\qquad\displaystyle 2= -\frac{1}{2}\cdot 1 + m \quad \Leftrightarrow \quad m = \frac{5}{2}\,$.

Normalen har ekvationen $\,\displaystyle y= -\frac{x}{2} + \frac{5}{2} = \frac{5-x}{2}\,$.

Exempel 14

Kurvan $\,y = 2 \, e^x - 3x\,$ har en tangent vars riktningskoefficient är $\,–1\,$. Bestäm tangeringspunkten.

Derivatan av högerledet är $\,y' = 2 \, e^x -3\,$ och i tangeringspunkten ska derivatan vara lika med $\,-1\,$, dvs. $\,y' = -1\,$, och detta ger oss ekvationen $$2 \, e^x - 3=-1 $$ som har lösningen $\,x=0\,$. I punkten $\,x=0\,$ har kurvan $\,y\,$-värdet $\,y(0) = 2 \, e^0 - 3 \cdot 0 = 2\,$ och därmed är tangeringspunkten $\,(0,2)\,$.

Den här artikeln är hämtad från http://wiki.math.se/wikis/sf0601_0701/index.php/1.1_Inledning_till_derivata

1.1 Inledning till derivata

Sommarmatte 2

Nuvarande version

[redigera] Inledning

[redigera] Derivatans definition

[redigera] Derivatans tecken

[redigera] Deriveringsregler

[redigera] Tangenter och normaler

Visningar

Personliga verktyg

Navigering

Sök

Verktygslåda

+__NOTOC__
 <table><tr><td width="600">
-<div class="inforuta">
+{{Info|
 '''Innehåll:'''
-* alt 1
+* Derivatans definition (översiktligt).
-* alt 2
+* Derivatan av $\,x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x$.
-</div>
+* Derivata av summa och differens.
+* Tangent och normal till kurvor.
+}}
+{{Info|
+'''Lärandemål:'''<br>
+Efter detta avsnitt ska du ha lärt dig att: <br>
+* Förstå derivatan $\,f^{\,\prime}(a)\,$ som lutningen av kurvan $\,y&#061;f(x)\,$ i punkten $\,x&#061;a\,$.
+* Förstå derivatan som den momentana ändringstakten av en storhet (exempelvis fart, prisökning, o.s.v.).
+* Veta att det finns funktioner som inte är deriverbara (t.ex. $\,f(x)&#061;\vert x\vert\,$ i $\,x&#061;0\,$).
+* Kunna derivera $x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x\,$ samt summor/differenser av sådana termer.
+* Kunna bestämma tangent och normal till $y&#061;f(x)$.
+* Veta att derivatan kan betecknas med $\,f^{\,\prime}(x)\,$ och $\,df/dx(x)\,$.
+}}
 [[1.1 Övningar|Övningar]]
 <!-- huvudtexten -->
-=Teori=
 ==Inledning==
-När man studerar matematiska funktioner och dess grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.
+När man studerar matematiska funktioner och deras grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.
-Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde ($y$) ändras för varje enhets ökning av variabelvärdet ($x$).
+Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde ($\,y\,$) ändras för varje enhets ökning av variabelvärdet ($\,x\,$).
 Om man känner till två punkter på en funktions graf kan man få ett mått på funktionens förändringsgrad mellan dessa punkter genom att beräkna ändringskvoten
-$$\frac{\Delta y}{\Delta x}= \frac{\textrm{skillnad i y-led}}{\textrm{skillnad i x-led}}$$
+$$\frac{\Delta y}{\Delta x}= \frac{\text{skillnad i y-led}}{\text{skillnad i x-led}}$$
 <div class="exempel">
 '''Exempel 1'''
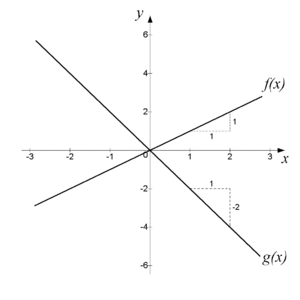
-De linjära funktionerna  $f(x)=x$ respektive $g(x)=-2x$  förändras på samma sätt hela tiden. Deras förändringsgrad är $1$ resp. $−2$, vilket vi känner till som linjernas respektive riktningskoefficient.
+De linjära funktionerna  $\,f(x)=x\,$ respektive $\,g(x)=-2x\,$ förändras på samma sätt hela tiden. Deras förändringsgrad är $\,1\,$ resp. $\,−2\,$, vilket vi känner till som linjernas respektive riktningskoefficient.
 [[Bild:X&-2x.gif|300px|center]]
 Om man har en funktion där funktionsvärdet förändras med tiden är det naturligt att använda begreppet förändringshastighet, eftersom förändringsgraden här anger hur funktionsvärdet ändras per tidsenhet.
-Om en bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, $s$ km,  efter $t$ timmar beskrivas med funktionen $s(t)=80 t$ .
+Om en bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, ''s'' km,  efter ''t'' timmar beskrivas med funktionen $\,s(t)=80 t\,$.
 Funktionens förändringsgrad anger hur funktionsvärdet ändras per timme, vilket naturligtvis är detsamma som bilens hastighet, 80 km/h.
 '''Exempel 2'''
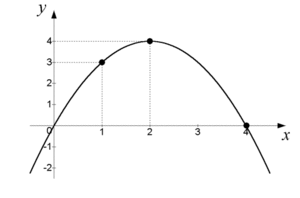
-För funktionen $f(x)=4x-x^2$ är $f(1)=3$ \, , \, $f(2)=4$  och $f(4)=0$ .
+För funktionen $\,f(x)=4x-x^2\,$ är $\,f(1)=3\,$,  $\,f(2)=4\,$ och $\,f(4)=0\,$.
-[[Bild:4x-x2.gif‎|200px|center]]
+[[Bild:4x-x2.gif‎|300px|center]]
-Medelförändringen (medellutningen) från $x = 1$ till $x = 2$ är
-$$\frac{\Delta y}{\Delta x}= \frac{f(2)-f(1)}{2-1} = \frac{4-3}{1}=1 \quad , \quad \textrm{funktionen ökar i detta intervall.}$$
-Medelförändringen från $x = 2$ till $x = 4$ är
+<ol type="a">
-$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(2)}{4-2}= \frac{0-4}{2}=-2 \quad , \quad \textrm{funktionen avtar i detta intervall.}$$
+  <li>Medelförändringen (medellutningen) från $\,x = 1\,$ till $\,x = 2\,$ är
+$$\frac{\Delta y}{\Delta x}= \frac{f(2)-f(1)}{2-1} = \frac{4-3}{1}=1\,\mbox{,}$$
+och funktionen ökar i detta intervall.<br><br></li>
-Mellan $x = 1$ och $x = 4$ är medelförändringen
+  <li>Medelförändringen från $\,x = 2\,$ till $\,x = 4\,$ är
-$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(1)}{4-1}= \frac{0-3}{3}=-1$$
+$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(2)}{4-2}= \frac{0-4}{2}=-2\,\mbox{,}$$
-dvs. i genomsnitt är funktionen avtagande i detta intervall (även om funktionen både växer och avtar i intervallet).
+och funktionen avtar i detta intervall.<br><br></li>
+  <li>Mellan $\,x = 1\,$ och $\,x = 4\,$ är medelförändringen
+$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(1)}{4-1}= \frac{0-3}{3}=-1\,\mbox{.}$$
+I genomsnitt är funktionen avtagande i detta intervall, även om funktionen både växer och avtar i intervallet.<br><br></li>
+</ol>
 </div>
 ==Derivatans definition==
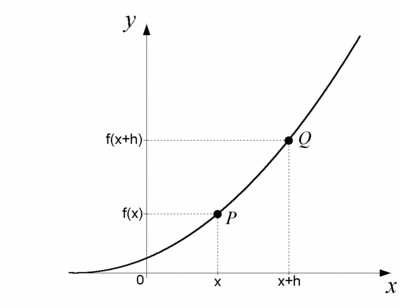
-För att beräkna den momentana förändringsgraden hos en funktion, dvs. funktionskurvans lutning i en punkt $P$, tar vi temporärt hjälp av ytterligare en punkt $Q$ i närheten av $P$ och bildar ändringskvoten mellan $P$ och $Q$:
+För att beräkna den momentana förändringsgraden hos en funktion, dvs. funktionskurvans lutning i en punkt $\,P\,$, tar vi temporärt hjälp av ytterligare en punkt $\,Q\,$ i närheten av $\,P\,$ och bildar ändringskvoten mellan $\,P\,$ och $\,Q\,$:
-<div class="exempel">
+[[Bild:Fxfx+h.gif|400px|center]]
-'''Exempel 3'''
-//illustration
+'''Ändringskvoten'''
 $$\frac{\Delta y}{\Delta x}= \frac{f(x+h)-f(x)}{(x+h)-x}= \frac{f(x+h)-f(x)}{h}$$
-</div>
-Om vi låter $Q$ närma sig $P (h \rightarrow 0)$ så kan vi lista ut vad värdet blir om punkterna sammanfaller och därmed få fram lutningen i punkten $P$. Vi kallar detta värde för $derivatan$ av $f(x)$ i punkten $P$, vilket kan tolkas som den momentana förändringsgraden av $f(x)$ i punkten $P$.
-Derivatan av en funktion $f(x)$ betecknas $f'(x)$  och kan formellt definieras så här:
-<div class="tips">
-$Derivatan$ av en funktion $f(x)$ , definieras som
-$$f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \,.$$
+Om vi låter $\,Q\,$ närma sig $\,P\,$ (dvs. låter $\,h \rightarrow 0\,$) så kan vi lista ut vad värdet blir om punkterna sammanfaller och därmed få fram lutningen i punkten $\,P\,$. Vi kallar detta värde för ''derivatan'' av $\,f(x)\,$ i punkten $\,P\,$, vilket kan tolkas som den momentana förändringsgraden av $\,f(x)\,$ i punkten $\,P\,$.
-Om $f'(x_0)$ existerar, säger man att $f(x)$ är $deriverbar$ i punkten $x_0$.
+Derivatan av en funktion $\,f(x)\,$ betecknas $\,f^{\,\prime}(x)\,$  och kan formellt definieras så här:
+<div class="regel">
+''Derivatan'' av en funktion $\,f(x)\,$, definieras som
+$$f^{\,\prime}(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \,.$$
+Om $\,f^{\,\prime}(x_0)\,$ existerar, säger man att $\,f(x)\,$ är ''deriverbar'' i punkten $\,x=x_0\,$.
 </div>
 !width="200" STYLE="border-bottom:2px solid grey;"|Derivata
 |-
-|$$f(x)$$
+|align="center" | $f(x)$
-|$$f'(x)$$
+|align="center" | $f^{\,\prime}(x)$
 |-
-|$$y$$
+|align="center" | $y$
-|$$y'$$
+|align="center" | $y^{\,\prime}$
 |-
-|$$y$$
+|align="center" | $y$
-|$$Dy$$
+|align="center" | $Dy$
 |-
-|$$y$$
+|align="center" | $y$
-|$$\frac{dy}{dx}$$
+|align="center" | $\displaystyle\frac{dy}{dx}$
 |-
-|$$s(t)$$
+|align="center" | $s(t)$
-|$$s'(t) \, , \, \frac{ds}{dt} \, , \, etc.$$
+|align="center" | $\dot s(t)$
 |}
 Derivatans tecken (+/−) visar oss om funktionens graf lutar uppåt eller nedåt, dvs. om funktionen är växande eller avtagande:
-{| class="wikitable" cellpadding="0px" cellspacing="0px" align="center"
-|-
+* $f^{\,\prime}(x)>0\,$ (positiv lutning) medför att $\,f(x)\,$ är växande.
-|width="100" style="text-align:left"|$$f'(x)>0$$
+* $f^{\,\prime}(x)<0\,$ (negativ lutning) medför att $\,f(x)\,$ är avtagande.
-|width="100" style="text-align:left"|(positiv lutning)
+* $f^{\,\prime}(x)=0\,$ (ingen lutning) medför att $\,f(x)\,$ är stationär (horisontell).
-|width="100" style="text-align:left"|$f(x)\, \mbox{är växande}$
-|-
-|width="100" style="text-align:left"|$$f'(x)<0$$
+<div class="exempel">
-|width="100" style="text-align:left"|(negativ lutning)
+'''Exempel 3'''
-|width="100" style="text-align:left"|$f(x) \, \mbox{är avtagande}$
-|-
+<ol type="a">
-|width="100" style="text-align:left"|$$f'(x)=0 $$
+  <li>$f(2)=3\ $ betyder att '''funktionens värde''' är $\,3\,$ när $\,x=2\,$.<br><br></li>
-|width="100" style="text-align:left"|(ingen lutning)
+  <li>$f^{\,\prime}(2)=3\ $ betyder att '''derivatans värde''' är $\,3\,$ när $\,x=2\,$, vilket i sin tur betyder att funktionens graf har lutningen $\,3\,$ när $\,x=2\,$.</li>
-|width="100" style="text-align:left"|$f(x)\,\mbox{är stationär (horistontell)}$
+</ol>
-|}
+</div>
 <div class="exempel">
 '''Exempel 4'''
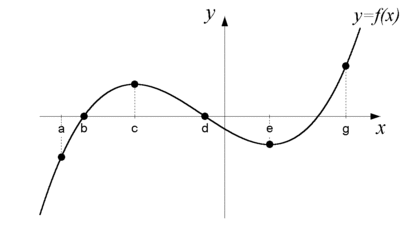
-$f(2)=3$ betyder att <u> funktionens värde </u> när $x=2$ är $3$
+I figuren kan man utläsa att
+{|
+|-
+| width=10% |
+| width=35% valign=center |
+$\displaystyle\eqalign{f^{\,\prime}(a) &> 0\cr f(b) &= 0\cr f^{\,\prime}(c) &= 0\cr  f(d) &= 0\cr f^{\,\prime}(e) &= 0\cr f(e) &< 0\cr f^{\,\prime}(g) &> 0} $
+| width=60% valign=top |
+[[Bild:F&f'.gif|400px]]
+| width=5% valign=top |
-$f'(2)=3$ betyder att <u> derivatans värde </u> när $x=2$ är $3$, vilket betyder att funktionens graf har lutningen $3$ när $x=2$
+|}
+Notera betydelsen av $\,f(x)\,$ respektive $\,f^{\,\prime}(x)\,$.
 </div>
 '''Exempel 5'''
-I figuren kan man utläsa att
+Temperaturen i en termos beskrivs av en funktion, där $\,T(t)\,$ är temperaturen i termosen efter $\,t\,$ minuter. Skriv följande med matematiska symboler:
-$$f'(a)>0$$
-$$f(b)=0$$
+<ol type="a">
-$$ f'(c) = 0 $$
+  <li>Efter 10&nbsp;minuter är temperaturen 80°.<br><br>
-$$ f(d) = 0 $$
+      $T(10)=80$<br><br></li>
-$$ f'(e) = 0 $$
+  <li>Efter 2&nbsp;minuter sjunker temperaturen i termosen med 3° per minut.<br><br>
-$$ f(e)<0$$
+      $T'(2)=-3\,$ (funktionen är avtagande, varför derivatan är negativ)<br><br></li>
-$$ f'(g) > 0 $$
+</ol>
+</div>
+<div class="exempel">
+'''Exempel 6'''
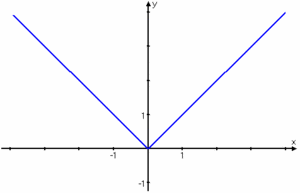
+Funktionen $\,f(x)=|x|\,$ saknar derivata då $\,x=0\,$. Man kan nämligen inte bestämma hur funktionens graf lutar i punkten $\,(0,0)\,$ (se figuren nedan).
+Man kan uttrycka detta på exempelvis något av följande sätt: "$\,f^{\,\prime}(0)\,$ existerar inte" , "$\,f^{\,\prime}(0)\,$ är ej definerad" eller "$\,f(x)\,$ är inte deriverbar i $\,x=0\,$".
-//Illustration
-Notera betydelsen av $f(x)$ respektive $f'(x)$.
+[[Bild:Absx.gif‎|300px|center]]
 </div>
+==Deriveringsregler==
+Med hjälp av derivatans definition kan man bestämma derivatan för de vanliga funktionstyperna.
 <div class="exempel">
-'''Exempel 6'''
+'''Exempel 7'''
-Temperaturen i en termos beskrivs av en funktion, där $T(t)$ är temperaturen i termosen efter $t$ minuter. Skriv följande med matematiska symboler:
+Om $\,f(x)=x^2\,$ så får vi enligt definitionen av derivata ändringskvoten
-<ol type="a">
+$$\frac{(x+h)^2-x^2}{h}=\frac{x^2+2hx+h^2-x^2}{h} = \frac{h(2x+h)}{h} = 2x + h\,\mbox{.}$$
-  <li>Efter $10$ minuter är temperaturen $80^\circ$
-  <li>Efter $2$ minuter sjunker temperaturen i termosen med $3^\circ$ per minut.
+Om vi sedan låter $\,h\,$ gå mot noll så ser vi att lutningen i punkten blir $\,2x\,$. Vi har därmed visat att lutningen i en godtycklig punkt på kurvan $\,y=x^2\,$ är $\,2x\,$, dvs. derivatan av $\,x^2\,$ är $\,2x\,$.
+</div>
+På liknande sätt kan man härleda allmänna deriveringsregler:
+{| BORDER="0" CELLPADDING="5" CELLSPACING="0" ALIGN="center"
+!width="200" style="border-bottom:2px solid grey;;"|Funktion
+!width="200" style="border-bottom:2px solid grey;"|Derivata
+|-
+|align="center"|$x^n$
+|align="center"|$n \cdot x^{n-1}$
+|-
+|align="center"|$\ln x$
+|align="center"|$1/x$
+|-
+|align="center"|$e^x$
+|align="center"|$e^x$
+|-
+|align="center"|$\sin x$
+|align="center"|$\cos x$
+|-
+|align="center"|$\cos x$
+|align="center"|$-\sin x$
+|-
+|align="center"|$\tan x$
+|align="center"|$1/\cos^2 x$
+|}
+Dessutom gäller för summor och differenser av funktionsuttryck att
+$$D(f(x) +g(x))= f^{\,\prime}(x) + g'(x)\,\mbox{.}$$
+Samt, om ''k'' är en konstant, att
+$$D(k \cdot f(x)) = k \cdot f^{\,\prime}(x)\,\mbox{.}$$
+<div class="exempel">
+'''Exempel 8'''
+<ol type="a">
+  <li> $D(2x^3 - 4x + 10 - \sin x) = 6x^2 - 4 + 0 - \cos x\,$. <br><br>
+  <li>$ y= 3 \ln x + 2e^x \quad$ ger att $\quad\displaystyle y'= 3 \cdot\frac{1}{x} + 2 e^x = \frac{3}{x} + 2 e^x\,$. <br><br>
+  <li>$\displaystyle \frac{d}{dx}\Bigl(\frac{3x^2}{5} - \frac{x^3}{2}\Bigr) = \frac{d}{dx}\bigl({\textstyle\frac{3}{5}}x^2 - {\textstyle\frac{1}{2}}x^3\bigr)= {\textstyle\frac{3}{5}}\cdot 2x - {\textstyle\frac{1}{2}}\cdot 3x^2= {\textstyle\frac{6}{5}}x - {\textstyle\frac{3}{2}}x^2\,$. <br><br>
+<li>$\displaystyle s(t)= v_0t + \frac{at^2}{2} \quad$ ger att $\quad\displaystyle s'(t)=v_0 + \frac{2at}{2} = v_0 + at\,$.
 </ol>
-''Lösning''
+</div>
+<div class="exempel">
+'''Exempel 9'''
 <ol type="a">
-  <li>$T(10)=80$
+  <li>$\displaystyle f(x) = \frac{1}{x} = x^{-1} \quad$ ger att $\quad\displaystyle f^{\,\prime}(x) = -1 \cdot x^{-2} = -\frac{1}{x^2}\,$. <br><br>
-  <li>$T'(2)=-3$ (funktionen är avtagande, varför derivatan är negativ)
+  <li>$\displaystyle f(x)= \frac{1}{3x^2} = {\textstyle\frac{1}{3}}\cdot x^{-2} \quad$ ger att $\quad\displaystyle f^{\,\prime}(x) = {\textstyle\frac{1}{3}}\cdot(-2)x^{-3} = -\frac{2}{3} \cdot x^{-3} = -\frac{2}{3x^3}\,$. <br><br>
+<li>$\displaystyle g(t) = \frac{t^2 - 2t + 1}{t} = t -2 + \frac{1}{t} \quad$ ger att $\quad\displaystyle g'(t) = 1 - \frac{1}{t^2}\,$. <br><br>
+<li>$\displaystyle y = \Bigl( x^2 + \frac{1}{x} \Bigr)^2 = (x^2)^2 + 2 \cdot x^2 \cdot \frac{1}{x} + \Bigl(\frac{1}{x} \Bigr)^2 = x^4 + 2x + x^{-2}$<br>
+$\qquad\quad$ ger att $\quad\displaystyle y' =4x^3 + 2 -2x^{-3} = 4x^3 + 2 - \frac{2}{x^3}\,$.
 </ol>
 <div class="exempel">
-'''Exempel 7'''
+'''Exempel 10'''
-Funktionen $ f(x)=|x|$ saknar derivata då $x=0$. Man kan nämligen inte bestämma hur funktionens graf lutar i punkten $(0,0)$ (se fig).<br>
+Funktionen $\,f(x)=x^2 + x^{-2}\,$ har derivatan
-Man kan uttrycka detta på exempelvis något av följande sätt: "$f´(0)$ existerar inte" , "$f'(0)$ är ej definerad" eller "$f(x)$ är inte deriverbar i $x=0$".
+$$f^{\,\prime}(x) = 2x^1 -2x^{-3} = 2x - \frac{2}{x^3}\,\mbox{.}$$
+Detta betyder exempelvis att $\,f^{\,\prime}(2) = 2\cdot 2 - 2/2^3= 4- \frac{1}{4} = \frac{15}{4}\,$ och att $\,f^{\,\prime}(-1) = 2 \cdot (-1) - 2/(-1)^3 = -2 + 2 = 0\,$. Däremot är derivatan $\,f'(0)\,$ inte definierad.
-//illustration
+</div>
+<div class="exempel">
+'''Exempel 11'''
+Ett föremål rör sig enligt $\,s(t) = t^3 -4t^2 +5t\,$, där $\,s(t)\,$ km är avståndet från startpunkten efter $\,t\,$ timmar.  Beräkna $\,s'(3)\,$ och förklara vad värdet står för.
+<br>
+<br>
+Tidsderivatan ges av
+$$s'(t) = 3t^2 - 8t +5\qquad\text{vilket ger att}\qquad s'(3) = 3 \cdot 3^2 - 8 \cdot 3 + 5 = 8\,\mbox{.}$$
+Detta kan tolkas som att efter 3 timmar är föremålets hastighet 8 km/h.
+</div>
+<div class="exempel">
+'''Exempel 12'''
+Totalkostnaden $\,T\,$ kr för tillverkning av $\,x\,$ gummidräkter ges av funktionen
+$$ T(x) = 40000 + 370x -0{,}09x^2 \quad \text{för} \ 0 \le x \le 200\,\mbox{.}$$
+Beräkna och förklara innebörden av nedanstående uttryck.
+<br>
+<br>
+<ol type="a">
+  <li>$T(120)$<br><br>
+      $T(120)=40000 + 370 \cdot 120 - 0{,}09 \cdot 120^2 = 83104\,$.<br>
+      Totalkostnaden för att tillverka 120 gummidräkter är 83104 kr.<br><br>
+  <li>$T'(120)$<br><br>
+      Derivatan ges av $\,T^{\,\prime}(x)= 370 - 0{,}18x\,$ och därför är $\,T^{\,\prime}(120) = 370 - 0{,}18 \cdot 120 \approx 348\,$.<br>
+      Marginalkostnaden ("kostnaden för att tillverka ytterligare 1 enhet") vid 120 tillverkade gummidräkter är approximativt 348 kr.<br><br>
+</ol>
 </div>
+==Tangenter och normaler==
+En ''tangent'' till en kurva är en rät linje som tangerar kurvan.
-<div class="inforuta">
+En ''normal'' till en kurva är en rät linje som är vinkelrät mot kurvan i en viss punkt på kurvan (och därmed också vinkelrät mot kurvans tangent i denna punkt).
-'''Råd för inläsning'''
-'''Tänk på att:'''
+För vinkelräta linjer gäller att produkten av deras riktningskoefficienter är $\,–1\,$, dvs. om tangentens riktningskoefficient betecknas $\,k_T\,$ och normalens $\,k_N\,$ så är $\,k_T \cdot k_N = -1\,$. Eftersom vi kan bestämma lutningen på en kurva med hjälp av derivatan så kan vi också bestämma ekvationen för en tangent eller en normal om vi känner till funktionsuttrycket för kurvan.
-text
-'''Lästips'''
+<div class="exempel">
+'''Exempel 13'''
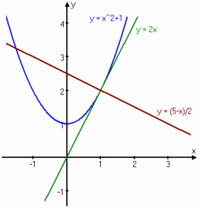
-stående
+Bestäm ekvationen för tangenten respektive normalen till kurvan $\,y=x^2 + 1\,$ i punkten $\,(1,2)\,$.
+<br>
+<br>
+[[Bild:Normal-tangent.gif‎|200px|right|]]
+Vi skriver tangentens ekvation som $\,y = kx + m\,$. Eftersom den ska tangera kurvan i $\,x=1\,$ har vi att $\,k= y'(1)\,$, dvs.
-'''Länktips'''
+$\qquad y' = 2x\,,\qquad y'(1) = 2\cdot 1 = 2\,$.
-stående
+Tangentlinjen ska också passerar genom punkten $\,(1,2)\,$ och därför måste $\,(1,2)\,$ uppfylla tangentens ekvation
-</div>
+$\qquad 2 = 2 \cdot 1 + m \quad \Leftrightarrow \quad m = 0\,$.
+Tangentens ekvation är alltså $\,y=2x\,$.
-''' © Copyright 2007, math.se'''
+Riktningskoefficienten för normalen är $\displaystyle k_N = -\frac{1}{k_T} = -\frac{1}{2}$ .
+Vidare går normalen också genom punkten $\,(1, 2)\,$ , dvs.
+$\qquad\displaystyle 2= -\frac{1}{2}\cdot 1 + m \quad \Leftrightarrow \quad m = \frac{5}{2}\,$.
+Normalen har ekvationen $\,\displaystyle y= -\frac{x}{2} + \frac{5}{2} = \frac{5-x}{2}\,$.
+</div>
+<div class="exempel">
+'''Exempel 14'''
+Kurvan $\,y = 2 \, e^x - 3x\,$ har en tangent vars riktningskoefficient är $\,–1\,$. Bestäm tangeringspunkten.
+<br>
+<br>
+Derivatan av högerledet är $\,y' = 2 \, e^x -3\,$ och i tangeringspunkten ska derivatan vara lika med $\,-1\,$, dvs.
+$\,y' = -1\,$, och detta  ger oss ekvationen
+$$2 \, e^x - 3=-1 $$
+som har lösningen $\,x=0\,$. I punkten $\,x=0\,$ har kurvan $\,y\,$-värdet $\,y(0) = 2 \, e^0 - 3 \cdot 0 = 2\,$ och därmed är tangeringspunkten $\,(0,2)\,$.
+</div>