1.1 Inledning till derivata

Sommarmatte 2

(Skillnad mellan versioner)

Hoppa till: navigering, sök

Versionen från 13 juni 2007 kl. 14.07

Innehåll:

Derivatans definition (översiktligt).
Derivatan av $\,x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x$.
Derivata av summa och differens.
Tangent och normal till kurvor.

Lärandemål:
Efter detta avsnitt ska du ha lärt dig att:

Förstå derivatan $\,f^{\,\prime}(a)\,$ som lutningen av kurvan $\,y=f(x)\,$ i punkten $\,x=a\,$.
Förstå derivatan som den momentana ändringstakten av en storhet (exempelvis fart, prisökning, o.s.v.).
Veta att det finns funktioner som inte är deriverbara (t.ex. $\,f(x)=\vert x\vert\,$ i $\,x=0\,$).
Kunna derivera $x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x\,$ samt summor/differenser av sådana termer.
Kunna bestämma tangent och normal till $y=f(x)$.
Veta att derivatan kan betecknas med $\,f^{\,\prime}(x)\,$ och $\,df/dx(x)\,$.

Övningar

Inledning

När man studerar matematiska funktioner och deras grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.

Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde ($\,y\,$) ändras för varje enhets ökning av variabelvärdet ($\,x\,$). Om man känner till två punkter på en funktions graf kan man få ett mått på funktionens förändringsgrad mellan dessa punkter genom att beräkna ändringskvoten

$$\frac{\Delta y}{\Delta x}= \frac{\text{skillnad i y-led}}{\text{skillnad i x-led}}$$

Exempel 1

De linjära funktionerna $\,f(x)=x\,$ respektive $\,g(x)=-2x\,$ förändras på samma sätt hela tiden. Deras förändringsgrad är $\,1\,$ resp. $\,−2\,$, vilket vi känner till som linjernas respektive riktningskoefficient.

För en linjär funktion gäller alltså att funktionens förändringsgrad är samma som linjens riktningskoefficient.

Om man har en funktion där funktionsvärdet förändras med tiden är det naturligt att använda begreppet förändringshastighet, eftersom förändringsgraden här anger hur funktionsvärdet ändras per tidsenhet.

Om en bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, s km, efter t timmar beskrivas med funktionen $\,s(t)=80 t\,$. Funktionens förändringsgrad anger hur funktionsvärdet ändras per timme, vilket naturligtvis är detsamma som bilens hastighet, 80 km/h.

För icke-linjära funktioner gäller ju att lutningen på funktionskurvan ändras hela tiden och därmed också funktionens förändringsgrad. För att bestämma hur en sådan funktion förändras kan vi antingen ange funktionens genomsnittliga förändring (medelförändringen) mellan två punkter på funktionskurvan, eller den momentana förändringsgraden i en punkt på kurvan.

Exempel 2

För funktionen $\,f(x)=4x-x^2\,$ är $\,f(1)=3\,$, $\,f(2)=4\,$ och $\,f(4)=0\,$.

Medelförändringen (medellutningen) från $\,x = 1\,$ till $\,x = 2\,$ är $$\frac{\Delta y}{\Delta x}= \frac{f(2)-f(1)}{2-1} = \frac{4-3}{1}=1\,\mbox{,}$$ och funktionen ökar i detta intervall.
Medelförändringen från $\,x = 2\,$ till $\,x = 4\,$ är $$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(2)}{4-2}= \frac{0-4}{2}=-2\,\mbox{,}$$ och funktionen avtar i detta intervall.
Mellan $\,x = 1\,$ och $\,x = 4\,$ är medelförändringen $$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(1)}{4-1}= \frac{0-3}{3}=-1\,\mbox{.}$$ I genomsnitt är funktionen avtagande i detta intervall, även om funktionen både växer och avtar i intervallet.

Derivatans definition

För att beräkna den momentana förändringsgraden hos en funktion, dvs. funktionskurvans lutning i en punkt $\,P\,$, tar vi temporärt hjälp av ytterligare en punkt $\,Q\,$ i närheten av $\,P\,$ och bildar ändringskvoten mellan $\,P\,$ och $\,Q\,$:

Derivatans definition: $$\frac{\Delta y}{\Delta x}= \frac{f(x+h)-f(x)}{(x+h)-x}= \frac{f(x+h)-f(x)}{h}$$

Om vi låter $\,Q\,$ närma sig $\,P\,$ (dvs. låter $\,h \rightarrow 0\,$) så kan vi lista ut vad värdet blir om punkterna sammanfaller och därmed få fram lutningen i punkten $\,P\,$. Vi kallar detta värde för derivatan av $\,f(x)\,$ i punkten $\,P\,$, vilket kan tolkas som den momentana förändringsgraden av $\,f(x)\,$ i punkten $\,P\,$.

Derivatan av en funktion $\,f(x)\,$ betecknas $\,f^{\,\prime}(x)\,$ och kan formellt definieras så här:

Derivatan av en funktion $\,f(x)\,$, definieras som $$f^{\,\prime}(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \,.$$ Om $\,f^{\,\prime}(x_0)\,$ existerar, säger man att $\,f(x)\,$ är deriverbar i punkten $\,x=x_0\,$.

Olika symboler för derivatan förekommer, t.ex.

Funktion	Derivata
$f(x)$	$f^{\,\prime}(x)$
$y$	$y^{\,\prime}$
$y$	$Dy$
$y$	$\displaystyle\frac{dy}{dx}$
$s(t)$	$\dot s(t)$

Derivatans tecken

Derivatans tecken (+/−) visar oss om funktionens graf lutar uppåt eller nedåt, dvs. om funktionen är växande eller avtagande:

$f^{\,\prime}(x)>0\,$ (positiv lutning) medför att $\,f(x)\,$ är växande.
$f^{\,\prime}(x)<0\,$ (negativ lutning) medför att $\,f(x)\,$ är avtagande.
$f^{\,\prime}(x)=0\,$ (ingen lutning) medför att $\,f(x)\,$ är stationär (horisontell).

Exempel 3

$f(2)=3\ $ betyder att funktionens värde är $\,3\,$ när $\,x=2\,$.
$f^{\,\prime}(2)=3\ $ betyder att derivatans värde är $\,3\,$ när $\,x=2\,$, vilket i sin tur betyder att funktionens graf har lutningen $\,3\,$ när $\,x=2\,$.

Exempel 4

I figuren kan man utläsa att

$\displaystyle\eqalign{f^{\,\prime}(a) &> 0\cr f(b) &= 0\cr f^{\,\prime}(c) &= 0\cr f(d) &= 0\cr f^{\,\prime}(e) &= 0\cr f(e) &< 0\cr f^{\,\prime}(g) &> 0} $

Notera betydelsen av $\,f(x)\,$ respektive $\,f^{\,\prime}(x)\,$.

Exempel 5

Temperaturen i en termos beskrivs av en funktion, där $\,T(t)\,$ är temperaturen i termosen efter $\,t\,$ minuter. Skriv följande med matematiska symboler:

Efter 10 minuter är temperaturen 80°.

$T(10)=80$
Efter 2 minuter sjunker temperaturen i termosen med 3° per minut.

$T'(2)=-3\,$ (funktionen är avtagande, varför derivatan är negativ)

Exempel 6

Funktionen $\,f(x)=|x|\,$ saknar derivata då $\,x=0\,$. Man kan nämligen inte bestämma hur funktionens graf lutar i punkten $\,(0,0)\,$ (se figuren nedan).

Man kan uttrycka detta på exempelvis något av följande sätt: "$\,f^{\,\prime}(0)\,$ existerar inte" , "$\,f^{\,\prime}(0)\,$ är ej definerad" eller "$\,f(x)\,$ är inte deriverbar i $\,x=0\,$".

Den här artikeln är hämtad från http://wiki.math.se/wikis/sf0601_0701/index.php/1.1_Inledning_till_derivata

 '''Lärandemål:'''<br>
 Efter detta avsnitt ska du ha lärt dig att: <br>
-* Förstå derivatan $\,f'(a)\,$ som lutningen av kurvan $\,y&#061;f(x)\,$ i punkten $\,x&#061;a\,$.
+* Förstå derivatan $\,f^{\,\prime}(a)\,$ som lutningen av kurvan $\,y&#061;f(x)\,$ i punkten $\,x&#061;a\,$.
-* Förstå derivatan som den momentana ändringstakten av en storhet (exempelvis fart, prisökning, ... ).
+* Förstå derivatan som den momentana ändringstakten av en storhet (exempelvis fart, prisökning, o.s.v.).
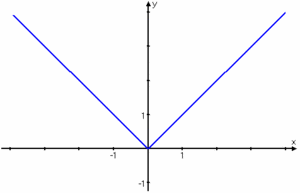
 * Veta att det finns funktioner som inte är deriverbara (t.ex. $\,f(x)&#061;\vert x\vert\,$ i $\,x&#061;0\,$).
-* Kunna derivera $x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x\,$ samt summor/differenser av sådan termer.
+* Kunna derivera $x^\alpha\,$, $\,\ln x\,$, $\,e^x\,$, $\,\cos x\,$, $\,\sin x\,$ och $\,\tan x\,$ samt summor/differenser av sådana termer.
 * Kunna bestämma tangent och normal till $y&#061;f(x)$.
-* Veta att derivatan kan betecknas med $f'(x)\,$ och $df/dx(x)$.
+* Veta att derivatan kan betecknas med $\,f^{\,\prime}(x)\,$ och $\,df/dx(x)\,$.
 }}
 ==Inledning==
-När man studerar matematiska funktioner och dess grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.
+När man studerar matematiska funktioner och deras grafer är ett av de viktigaste områdena studiet av en funktions förändring, dvs. om en funktion ökar eller minskar samt i vilken takt detta sker.
-Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde ($y$) ändras för varje enhets ökning av variabelvärdet ($x$).
+Man använder sig här av begreppet förändringsgrad (eller förändringshastighet), vilket är ett mått på hur funktionens värde ($\,y\,$) ändras för varje enhets ökning av variabelvärdet ($\,x\,$).
 Om man känner till två punkter på en funktions graf kan man få ett mått på funktionens förändringsgrad mellan dessa punkter genom att beräkna ändringskvoten
-$$\frac{\Delta y}{\Delta x}= \frac{\textrm{skillnad i y-led}}{\textrm{skillnad i x-led}}$$
+$$\frac{\Delta y}{\Delta x}= \frac{\text{skillnad i y-led}}{\text{skillnad i x-led}}$$
 <div class="exempel">
 '''Exempel 1'''
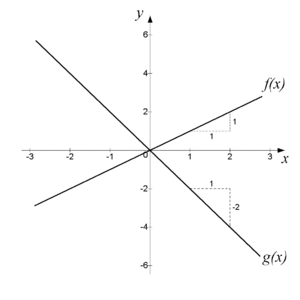
-De linjära funktionerna  $f(x)=x$ respektive $g(x)=-2x$  förändras på samma sätt hela tiden. Deras förändringsgrad är $1$ resp. $−2$, vilket vi känner till som linjernas respektive riktningskoefficient.
+De linjära funktionerna  $\,f(x)=x\,$ respektive $\,g(x)=-2x\,$ förändras på samma sätt hela tiden. Deras förändringsgrad är $\,1\,$ resp. $\,−2\,$, vilket vi känner till som linjernas respektive riktningskoefficient.
 [[Bild:X&-2x.gif|300px|center]]
 Om man har en funktion där funktionsvärdet förändras med tiden är det naturligt att använda begreppet förändringshastighet, eftersom förändringsgraden här anger hur funktionsvärdet ändras per tidsenhet.
-Om en bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, $s$ km,  efter $t$ timmar beskrivas med funktionen $s(t)=80 t$ .
+Om en bil rör sig med hastigheten 80 km/h så kan den tillryggalagda sträckan, ''s'' km,  efter ''t'' timmar beskrivas med funktionen $\,s(t)=80 t\,$.
 Funktionens förändringsgrad anger hur funktionsvärdet ändras per timme, vilket naturligtvis är detsamma som bilens hastighet, 80 km/h.
 '''Exempel 2'''
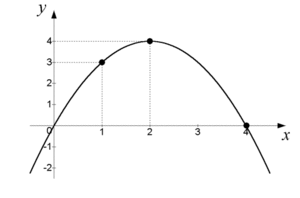
-För funktionen $f(x)=4x-x^2$ är $f(1)=3$ ,  $f(2)=4$  och $f(4)=0$ .
+För funktionen $\,f(x)=4x-x^2\,$ är $\,f(1)=3\,$,  $\,f(2)=4\,$ och $\,f(4)=0\,$.
 [[Bild:4x-x2.gif‎|300px|center]]
-Medelförändringen (medellutningen) från $x = 1$ till $x = 2$ är
-$$\frac{\Delta y}{\Delta x}= \frac{f(2)-f(1)}{2-1} = \frac{4-3}{1}=1 \quad , \quad \textrm{funktionen ökar i detta intervall.}$$
-Medelförändringen från $x = 2$ till $x = 4$ är
+<ol type="a">
-$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(2)}{4-2}= \frac{0-4}{2}=-2 \quad , \quad \textrm{funktionen avtar i detta intervall.}$$
+  <li>Medelförändringen (medellutningen) från $\,x = 1\,$ till $\,x = 2\,$ är
+$$\frac{\Delta y}{\Delta x}= \frac{f(2)-f(1)}{2-1} = \frac{4-3}{1}=1\,\mbox{,}$$
+och funktionen ökar i detta intervall.<br><br></li>
-Mellan $x = 1$ och $x = 4$ är medelförändringen
+  <li>Medelförändringen från $\,x = 2\,$ till $\,x = 4\,$ är
-$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(1)}{4-1}= \frac{0-3}{3}=-1$$
+$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(2)}{4-2}= \frac{0-4}{2}=-2\,\mbox{,}$$
-dvs. i genomsnitt är funktionen avtagande i detta intervall (även om funktionen både växer och avtar i intervallet).
+och funktionen avtar i detta intervall.<br><br></li>
+  <li>Mellan $\,x = 1\,$ och $\,x = 4\,$ är medelförändringen
+$$\frac{\Delta y}{\Delta x}= \frac{f(4)-f(1)}{4-1}= \frac{0-3}{3}=-1\,\mbox{.}$$
+I genomsnitt är funktionen avtagande i detta intervall, även om funktionen både växer och avtar i intervallet.<br><br></li>
+</ol>
 </div>
 ==Derivatans definition==
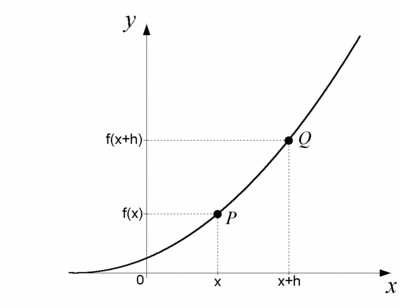
-För att beräkna den momentana förändringsgraden hos en funktion, dvs. funktionskurvans lutning i en punkt $P$, tar vi temporärt hjälp av ytterligare en punkt $Q$ i närheten av $P$ och bildar ändringskvoten mellan $P$ och $Q$:
+För att beräkna den momentana förändringsgraden hos en funktion, dvs. funktionskurvans lutning i en punkt $\,P\,$, tar vi temporärt hjälp av ytterligare en punkt $\,Q\,$ i närheten av $\,P\,$ och bildar ändringskvoten mellan $\,P\,$ och $\,Q\,$:
 [[Bild:Fxfx+h.gif|400px|center]]
 </div>
-Om vi låter $Q$ närma sig $P (h \rightarrow 0)$ så kan vi lista ut vad värdet blir om punkterna sammanfaller och därmed få fram lutningen i punkten $P$. Vi kallar detta värde för $derivatan$ av $f(x)$ i punkten $P$, vilket kan tolkas som den momentana förändringsgraden av $f(x)$ i punkten $P$.
+Om vi låter $\,Q\,$ närma sig $\,P\,$ (dvs. låter $\,h \rightarrow 0\,$) så kan vi lista ut vad värdet blir om punkterna sammanfaller och därmed få fram lutningen i punkten $\,P\,$. Vi kallar detta värde för ''derivatan'' av $\,f(x)\,$ i punkten $\,P\,$, vilket kan tolkas som den momentana förändringsgraden av $\,f(x)\,$ i punkten $\,P\,$.
-Derivatan av en funktion $f(x)$ betecknas $f'(x)$  och kan formellt definieras så här:
+Derivatan av en funktion $\,f(x)\,$ betecknas $\,f^{\,\prime}(x)\,$  och kan formellt definieras så här:
 <div class="tips">
+''Derivatan'' av en funktion $\,f(x)\,$, definieras som
-$Derivatan$ av en funktion $f(x)$ , definieras som
+$$f^{\,\prime}(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \,.$$
+Om $\,f^{\,\prime}(x_0)\,$ existerar, säger man att $\,f(x)\,$ är ''deriverbar'' i punkten $\,x=x_0\,$.
-$$f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \,.$$
-Om $f'(x_0)$ existerar, säger man att $f(x)$ är $deriverbar$ i punkten $x_0$.
 </div>
 !width="200" STYLE="border-bottom:2px solid grey;"|Derivata
 |-
-|$$f(x)$$
+|align="center" | $f(x)$
-|$$f'(x)$$
+|align="center" | $f^{\,\prime}(x)$
 |-
-|$$y$$
+|align="center" | $y$
-|$$y'$$
+|align="center" | $y^{\,\prime}$
 |-
-|$$y$$
+|align="center" | $y$
-|$$Dy$$
+|align="center" | $Dy$
 |-
-|$$y$$
+|align="center" | $y$
-|$$\frac{dy}{dx}$$
+|align="center" | $\displaystyle\frac{dy}{dx}$
 |-
-|$$s(t)$$
+|align="center" | $s(t)$
-|$$s'(t) \, , \, \frac{ds}{dt} \, , \, etc.$$
+|align="center" | $\dot s(t)$
 |}
 Derivatans tecken (+/−) visar oss om funktionens graf lutar uppåt eller nedåt, dvs. om funktionen är växande eller avtagande:
-{| class="wikitable" cellpadding="0px" cellspacing="0px" align="center"
-|-
+* $f^{\,\prime}(x)>0\,$ (positiv lutning) medför att $\,f(x)\,$ är växande.
-|width="100" style="text-align:left"|$$f'(x)>0$$
+* $f^{\,\prime}(x)<0\,$ (negativ lutning) medför att $\,f(x)\,$ är avtagande.
-|width="100" style="text-align:left"|(positiv lutning)
+* $f^{\,\prime}(x)=0\,$ (ingen lutning) medför att $\,f(x)\,$ är stationär (horisontell).
-|width="100" style="text-align:left"|$f(x)\, \mbox{är växande}$
-|-
-|width="100" style="text-align:left"|$$f'(x)<0$$
-|width="100" style="text-align:left"|(negativ lutning)
-|width="100" style="text-align:left"|$f(x) \, \mbox{är avtagande}$
-|-
-|width="100" style="text-align:left"|$$f'(x)=0 $$
-|width="100" style="text-align:left"|(ingen lutning)
-|width="100" style="text-align:left"|$f(x)\,\mbox{är stationär (horistontell)}$
-|}
 <div class="exempel">
 '''Exempel 3'''
-$f(2)=3$ betyder att <u> funktionens värde </u> när $x=2$ är $3$
+<ol type="a">
+  <li>$f(2)=3\ $ betyder att '''funktionens värde''' är $\,3\,$ när $\,x=2\,$.<br><br></li>
+  <li>$f^{\,\prime}(2)=3\ $ betyder att '''derivatans värde''' är $\,3\,$ när $\,x=2\,$, vilket i sin tur betyder att funktionens graf har lutningen $\,3\,$ när $\,x=2\,$.</li>
-$f'(2)=3$ betyder att <u> derivatans värde </u> när $x=2$ är $3$, vilket betyder att funktionens graf har lutningen $3$ när $x=2$
+</ol>
 </div>
 {|
 |-
-| width=35% valign=top |
+| width=10% |
-$$f'(a)>0$$
+| width=35% valign=center |
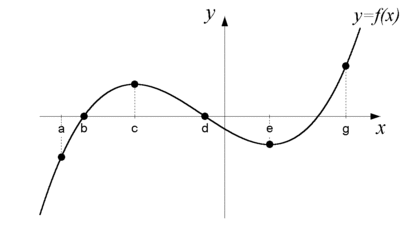
-$$f(b)=0$$
+$\displaystyle\eqalign{f^{\,\prime}(a) &> 0\cr f(b) &= 0\cr f^{\,\prime}(c) &= 0\cr  f(d) &= 0\cr f^{\,\prime}(e) &= 0\cr f(e) &< 0\cr f^{\,\prime}(g) &> 0} $
-$$ f'(c) = 0 $$
-$$ f(d) = 0 $$
-$$ f'(e) = 0 $$
-$$ f(e)<0$$
-$$ f'(g) > 0 $$
 | width=60% valign=top |
 [[Bild:F&f'.gif|400px]]
 |}
-Notera betydelsen av $f(x)$ respektive $f'(x)$.
+Notera betydelsen av $\,f(x)\,$ respektive $\,f^{\,\prime}(x)\,$.
 </div>
 '''Exempel 5'''
-Temperaturen i en termos beskrivs av en funktion, där $T(t)$ är temperaturen i termosen efter $t$ minuter. Skriv följande med matematiska symboler:
+Temperaturen i en termos beskrivs av en funktion, där $\,T(t)\,$ är temperaturen i termosen efter $\,t\,$ minuter. Skriv följande med matematiska symboler:
 <ol type="a">
-  <li>Efter $10$ minuter är temperaturen $80^\circ$
+  <li>Efter 10&nbsp;minuter är temperaturen 80°.<br><br>
-  <li>Efter $2$ minuter sjunker temperaturen i termosen med $3^\circ$ per minut.
+      $T(10)=80$<br><br></li>
+  <li>Efter 2&nbsp;minuter sjunker temperaturen i termosen med 3° per minut.<br><br>
+      $T'(2)=-3\,$ (funktionen är avtagande, varför derivatan är negativ)<br><br></li>
 </ol>
-'''Lösning'''
-<ol type="a">
-  <li>$T(10)=80$
-  <li>$T'(2)=-3$ (funktionen är avtagande, varför derivatan är negativ)
-</ol>
 </div>
 '''Exempel 6'''
-Funktionen $ f(x)=|x|$ saknar derivata då $x=0$. Man kan nämligen inte bestämma hur funktionens graf lutar i punkten $(0,0)$ (se fig).<br>
+Funktionen $\,f(x)=|x|\,$ saknar derivata då $\,x=0\,$. Man kan nämligen inte bestämma hur funktionens graf lutar i punkten $\,(0,0)\,$ (se figuren nedan).
-Man kan uttrycka detta på exempelvis något av följande sätt: "$f´(0)$ existerar inte" , "$f'(0)$ är ej definerad" eller "$f(x)$ är inte deriverbar i $x=0$".
+Man kan uttrycka detta på exempelvis något av följande sätt: "$\,f^{\,\prime}(0)\,$ existerar inte" , "$\,f^{\,\prime}(0)\,$ är ej definerad" eller "$\,f(x)\,$ är inte deriverbar i $\,x=0\,$".

1.1 Inledning till derivata

Sommarmatte 2

Versionen från 13 juni 2007 kl. 14.07

Inledning

Derivatans definition

Derivatans tecken

Visningar

Personliga verktyg

Navigering

Sök

Verktygslåda