1.1 Inledning till derivata
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 13 juni 2007 kl. 14.07 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) m (flyttade 1.1 Inledning derivata till 1.1 Inledning till derivata) ← Gå till föregående ändring |
Versionen från 13 juni 2007 kl. 14.39 (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) (Lagt till avsnitten "Deriveringsregler" och "Tangenter och normaler") Gå till nästa ändring → |
||
| Rad 185: | Rad 185: | ||
| </div> | </div> | ||
| + | ==Deriveringsregler== | ||
| + | Med hjälp av derivatans definition kan man bestämma derivatan för de vanliga funktionstyperna. | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 1''' | ||
| + | |||
| + | Om $\,f(x)=x^2\,$ så får vi enligt definitionen av derivata ändringskvoten | ||
| + | |||
| + | $$\frac{(x+h)^2-x^2}{h}=\frac{x^2+2hx+h^2-x^2}{h} = \frac{h(2x+h)}{h} = 2x + h\,\mbox{.}$$ | ||
| + | |||
| + | Om vi sedan låter $\,h\,$ gå mot noll så ser vi att lutningen i punkten blir $\,2x\,$. Vi har därmed visat att lutningen i en godtycklig punkt på kurvan $\,y=x^2\,$ är $\,2x\,$, dvs. derivatan av $\,x^2\,$ är $\,2x\,$. | ||
| + | </div> | ||
| + | |||
| + | På liknande sätt kan man härleda allmänna deriveringsregler: | ||
| + | |||
| + | {| BORDER="0" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | ||
| + | !width="200" style="border-bottom:2px solid grey;;"|Funktion | ||
| + | !width="200" style="border-bottom:2px solid grey;"|Derivata | ||
| + | |- | ||
| + | |align="center"|$x^n$ | ||
| + | |align="center"|$n \cdot x^{n-1}$ | ||
| + | |- | ||
| + | |align="center"|$\ln x$ | ||
| + | |align="center"|$1/x$ | ||
| + | |- | ||
| + | |align="center"|$e^x$ | ||
| + | |align="center"|$e^x$ | ||
| + | |- | ||
| + | |align="center"|$\sin x$ | ||
| + | |align="center"|$\cos x$ | ||
| + | |- | ||
| + | |align="center"|$\cos x$ | ||
| + | |align="center"|$-\sin x$ | ||
| + | |- | ||
| + | |align="center"|$\tan x$ | ||
| + | |align="center"|$1/\cos^2 x$ | ||
| + | |} | ||
| + | |||
| + | |||
| + | Dessutom gäller för summor och differenser av funktionsuttryck att | ||
| + | $$D(f(x) +g(x))= f'(x) + g'(x)\,\mbox{.}$$ | ||
| + | |||
| + | Samt, om ''k'' är en konstant, att | ||
| + | $$D(k \cdot f(x)) = k \cdot f'(x)\,\mbox{.}$$ | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 2''' | ||
| + | <ol type="a"> | ||
| + | <li> $D(2x^3 - 4x + 10 - \sin x) = 6x^2 - 4 + 0 - \cos x$ <br><br> | ||
| + | <li>$ y= 3 \ln x + 2e^x \quad$ ger att $\,\displaystyle y'= 3 \cdot\frac{1}{x} + 2 e^x = \frac{3}{x} + 2 e^x$ <br><br> | ||
| + | <li>$\displaystyle \frac{d}{dx}\Bigl(\frac{3x^2}{5} - \frac{x^3}{2}\Bigr) = \frac{d}{dx}\bigl({\textstyle\frac{3}{5}}x^2 - {\textstyle\frac{1}{2}}x^3\bigr)= {\textstyle\frac{3}{5}}\cdot 2x - {\\textstyle\frac{1}{2}}\cdot 3x^2= {\textstyle\frac{6}{5}}x - {\textstyle\frac{3}{2}}x^2$ <br><br> | ||
| + | <li>$\displaystyle s(t)= v_0t + \frac{at^2}{2} \quad$ ger att $\displaystyle s'(t)=v_0 + \frac{2at}{2} = v_0 + at$ | ||
| + | </ol> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 3''' | ||
| + | <ol type="a"> | ||
| + | <li>$\displaystyle f(x) = \frac{1}{x} = x^{-1} \quad$ ger att $\displaystyle f'(x) = -1 \cdot x^{-2} = -\frac{1}{x^2}$ <br><br> | ||
| + | <li>$\displaystyle f(x)= \frac{1}{3x^2} = \frac{1}{3} \cdot x^{-2} \quad$ ger att $\displaystyle f'(x) = {\textstyle\frac{1}{3}}\cdot(-2)x^{-3} = -\frac{2}{3} \cdot x^{-3} = -\frac{2}{3x^3} $ <br><br> | ||
| + | <li>$\displaystyle g(t) = \frac{t^2 - 2t + 1}{t} = t -2 + \frac{1}{t} \quad$ ger att $g'(t) = 1 - \frac{1}{t^2}$ <br><br> | ||
| + | <li>$\displaystyle y = \left( x^2 + \frac{1}{x} \right)^2 = (x^2)^2 + 2 \cdot x^2 \cdot \frac{1}{x} + \left(\frac{1}{x} \right)^2 = x^4 + 2x + x^{-2} \quad$<br> | ||
| + | $\qquad\quad$ ger att $\displaystyle y' =4x^3 + 2 -2x^{-3} = 4x^3 + 2 - \frac{2}{x^3}$ | ||
| + | </ol> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 4''' | ||
| + | |||
| + | Funktionen $\,f(x)=x^2 + x^{-2}\,$ har derivatan $\displaystyle \,f'(x) = 2x^1 -2x^{-3} = 2x - \frac{2}{x^3}$. Detta betyder att | ||
| + | |||
| + | * $\displaystyle f'(2) = 2\cdot 2 - \frac{2}{2^3}= 4- \frac{1}{4} = \frac{15}{4}$<br><br> | ||
| + | * $\displaystyle f'(-1) = 2 \cdot (-1) - \frac{2}{(-1)^3} = -2 + 2 = 0$<br><br> | ||
| + | * $ f'(0) =$ ej def. | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 5''' | ||
| + | |||
| + | Ett föremål rör sig enligt $\,s(t) = t^3 -4t^2 +5t\,$, där $\,s(t)\,$ km är avståndet från startpunkten efter $\,t\,$ timmar. Beräkna $\,s'(3)\,$ och förklara vad värdet står för. | ||
| + | <br> | ||
| + | <br> | ||
| + | Tidsderivatan ges av | ||
| + | $$s'(t) = 3t^2 - 8t +5\qquad\text{vilket ger att}\qquad s'(3) = 3 \cdot 3^2 - 8 \cdot 3 + 5 = 8\,\mbox{.}$$ | ||
| + | Detta kan tolkas som att efter 3 timmar är föremålets hastighet 8 km/h. | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 6''' | ||
| + | |||
| + | Totalkostnaden $\,T\,$ kr för tillverkning av $\,x\,$ gummidräkter ges av funktionen | ||
| + | $$ T(x) = 40000 + 370x -0{,}09x^2 \quad \text{för} \ 0 \le x \le 200\,\mbox{.}$$ | ||
| + | |||
| + | Beräkna och förklara | ||
| + | <ol type="a"> | ||
| + | <li>$T(120)$<br><br> | ||
| + | $T(120)=40000 + 370 \cdot 120 - 0{,}09 \cdot 120^2 = 83104$ <br> | ||
| + | Totalkostnaden för att tillverka 120 gummidräkter är 83104 kr. <br><br> | ||
| + | <li>$T'(120)$<br><br> | ||
| + | $T'(x)= 370 - 0{,}18x$ <br> | ||
| + | $T'(120) = 370 - 0{,}18 \cdot 120 \approx 348$ <br> | ||
| + | Marginalkostnaden ("kostnaden för att tillverka ytterligare 1 enhet") vid 120 tillverkade gummidräkter är approximativt 348 kr.<br><br> | ||
| + | </ol> | ||
| + | |||
| + | </div> | ||
| + | |||
| + | ==Tangenter och normaler== | ||
| + | En ''tangent'' till en kurva är en rät linje som tangerar kurvan. | ||
| + | |||
| + | En ''normal'' till en kurva är en rät linje som är vinkelrät mot kurvan i en viss punkt på kurvan (och därmed också vinkelrät mot kurvans tangent i denna punkt). | ||
| + | |||
| + | För vinkelräta linjer gäller att produkten av deras riktningskoefficienter är $\,–1\,$, dvs. om tangentens riktningskoefficient betecknas $\,k_T\,$ och normalens $\,k_N\,$ så är $\,k_T \cdot k_N = -1\,$. Eftersom vi kan bestämma lutningen på en kurva med hjälp av derivatan så kan vi också bestämma ekvationen för en tangent eller normal om vi känner till funktionsuttrycket för kurvan. | ||
| + | |||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 7''' | ||
| + | |||
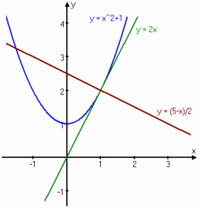
| + | Bestäm ekvationen för tangenten respektive normalen till kurvan $\,y=x^2 + 1\,$ i punkten $\,(1,2)\,$. | ||
| + | |||
| + | |||
| + | '''Lösning''' | ||
| + | |||
| + | [[Bild:Normal-tangent.gif|200px|right|]] | ||
| + | Tangentens ekvation är $\,y = kx + m\,$, där $\,k= y'(1)\,$. | ||
| + | |||
| + | $y' = 2x\,,\qquad y'(1) = 2\cdot 1 = 2\,$. | ||
| + | |||
| + | Eftersom linjen också passerar punkten $\,(1,2)\,$ har vi att | ||
| + | |||
| + | $2 = 2 \cdot 1 + m \quad \rightarrow \quad m = 0\,$. | ||
| + | |||
| + | Tangentens ekvation är alltså $\,y=2x\,$. | ||
| + | |||
| + | |||
| + | Riktningskoefficienten för normalen är $\displaystyle k_N = -\frac{1}{k_T} = -\frac{1}{2}$ . | ||
| + | |||
| + | Normalen går också genom punkten $\,(1, 2)\,$ , dvs. | ||
| + | |||
| + | $2= -\displaystyle \frac{1}{2}\cdot 1 + m \quad \rightarrow \quad m = \displaystyle \frac{5}{2}\,$. | ||
| + | |||
| + | Normalen har ekvationen $\,y= -\displaystyle \frac{x}{2} + \displaystyle \frac{5}{2} = \displaystyle \frac{5-x}{2}\,$. | ||
| + | |||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 8''' | ||
| + | |||
| + | Kurvan $\,y = 2 \, e^x - 3x\,$ har en tangent vars riktningskoefficient är $\,–1\,$. Bestäm tangeringspunkten. | ||
| + | |||
| + | |||
| + | '''Lösning''' | ||
| + | |||
| + | $y' = 2 \, e^x -3$ | ||
| + | |||
| + | $ y' = -1 \quad \rightarrow \quad 2 \, e^x = 2 \quad \rightarrow \quad x=0$ | ||
| + | |||
| + | $ y(0) = 2 \, e^0 - 3 \cdot 0 = 2 $ | ||
| + | |||
| + | Tangeringspunkten är $\,(0,2)\,$. | ||
| + | |||
| + | </div> | ||