1.1 Inledning till derivata
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 13 juni 2007 kl. 14.39 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Lagt till avsnitten "Deriveringsregler" och "Tangenter och normaler") ← Gå till föregående ändring |
Versionen från 14 juni 2007 kl. 08.13 (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst) Gå till nästa ändring → |
||
| Rad 189: | Rad 189: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 1''' | + | '''Exempel 7''' |
| Om $\,f(x)=x^2\,$ så får vi enligt definitionen av derivata ändringskvoten | Om $\,f(x)=x^2\,$ så får vi enligt definitionen av derivata ändringskvoten | ||
| Rad 225: | Rad 225: | ||
| Dessutom gäller för summor och differenser av funktionsuttryck att | Dessutom gäller för summor och differenser av funktionsuttryck att | ||
| - | $$D(f(x) +g(x))= f'(x) + g'(x)\,\mbox{.}$$ | + | $$D(f(x) +g(x))= f^{\,\prime}(x) + g'(x)\,\mbox{.}$$ |
| Samt, om ''k'' är en konstant, att | Samt, om ''k'' är en konstant, att | ||
| - | $$D(k \cdot f(x)) = k \cdot f'(x)\,\mbox{.}$$ | + | $$D(k \cdot f(x)) = k \cdot f^{\,\prime}(x)\,\mbox{.}$$ |
| + | |||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 2''' | + | '''Exempel 8''' |
| <ol type="a"> | <ol type="a"> | ||
| - | <li> $D(2x^3 - 4x + 10 - \sin x) = 6x^2 - 4 + 0 - \cos x$ <br><br> | + | <li> $D(2x^3 - 4x + 10 - \sin x) = 6x^2 - 4 + 0 - \cos x\,$. <br><br> |
| - | <li>$ y= 3 \ln x + 2e^x \quad$ ger att $\,\displaystyle y'= 3 \cdot\frac{1}{x} + 2 e^x = \frac{3}{x} + 2 e^x$ <br><br> | + | <li>$ y= 3 \ln x + 2e^x \quad$ ger att $\quad\displaystyle y'= 3 \cdot\frac{1}{x} + 2 e^x = \frac{3}{x} + 2 e^x\,$. <br><br> |
| - | <li>$\displaystyle \frac{d}{dx}\Bigl(\frac{3x^2}{5} - \frac{x^3}{2}\Bigr) = \frac{d}{dx}\bigl({\textstyle\frac{3}{5}}x^2 - {\textstyle\frac{1}{2}}x^3\bigr)= {\textstyle\frac{3}{5}}\cdot 2x - {\\textstyle\frac{1}{2}}\cdot 3x^2= {\textstyle\frac{6}{5}}x - {\textstyle\frac{3}{2}}x^2$ <br><br> | + | <li>$\displaystyle \frac{d}{dx}\Bigl(\frac{3x^2}{5} - \frac{x^3}{2}\Bigr) = \frac{d}{dx}\bigl({\textstyle\frac{3}{5}}x^2 - {\textstyle\frac{1}{2}}x^3\bigr)= {\textstyle\frac{3}{5}}\cdot 2x - {\textstyle\frac{1}{2}}\cdot 3x^2= {\textstyle\frac{6}{5}}x - {\textstyle\frac{3}{2}}x^2\,$. <br><br> |
| - | <li>$\displaystyle s(t)= v_0t + \frac{at^2}{2} \quad$ ger att $\displaystyle s'(t)=v_0 + \frac{2at}{2} = v_0 + at$ | + | <li>$\displaystyle s(t)= v_0t + \frac{at^2}{2} \quad$ ger att $\quad\displaystyle s'(t)=v_0 + \frac{2at}{2} = v_0 + at\,$. |
| </ol> | </ol> | ||
| Rad 242: | Rad 243: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 3''' | + | '''Exempel 9''' |
| <ol type="a"> | <ol type="a"> | ||
| - | <li>$\displaystyle f(x) = \frac{1}{x} = x^{-1} \quad$ ger att $\displaystyle f'(x) = -1 \cdot x^{-2} = -\frac{1}{x^2}$ <br><br> | + | <li>$\displaystyle f(x) = \frac{1}{x} = x^{-1} \quad$ ger att $\quad\displaystyle f^{\,\prime}(x) = -1 \cdot x^{-2} = -\frac{1}{x^2}\,$. <br><br> |
| - | <li>$\displaystyle f(x)= \frac{1}{3x^2} = \frac{1}{3} \cdot x^{-2} \quad$ ger att $\displaystyle f'(x) = {\textstyle\frac{1}{3}}\cdot(-2)x^{-3} = -\frac{2}{3} \cdot x^{-3} = -\frac{2}{3x^3} $ <br><br> | + | <li>$\displaystyle f(x)= \frac{1}{3x^2} = {\textstyle\frac{1}{3}}\cdot x^{-2} \quad$ ger att $\quad\displaystyle f^{\,\prime}(x) = {\textstyle\frac{1}{3}}\cdot(-2)x^{-3} = -\frac{2}{3} \cdot x^{-3} = -\frac{2}{3x^3}\,$. <br><br> |
| - | <li>$\displaystyle g(t) = \frac{t^2 - 2t + 1}{t} = t -2 + \frac{1}{t} \quad$ ger att $g'(t) = 1 - \frac{1}{t^2}$ <br><br> | + | <li>$\displaystyle g(t) = \frac{t^2 - 2t + 1}{t} = t -2 + \frac{1}{t} \quad$ ger att $\quad\displaystyle g'(t) = 1 - \frac{1}{t^2}\,$. <br><br> |
| - | <li>$\displaystyle y = \left( x^2 + \frac{1}{x} \right)^2 = (x^2)^2 + 2 \cdot x^2 \cdot \frac{1}{x} + \left(\frac{1}{x} \right)^2 = x^4 + 2x + x^{-2} \quad$<br> | + | <li>$\displaystyle y = \Bigl( x^2 + \frac{1}{x} \Bigr)^2 = (x^2)^2 + 2 \cdot x^2 \cdot \frac{1}{x} + \Bigl(\frac{1}{x} \Bigr)^2 = x^4 + 2x + x^{-2}$<br> |
| - | $\qquad\quad$ ger att $\displaystyle y' =4x^3 + 2 -2x^{-3} = 4x^3 + 2 - \frac{2}{x^3}$ | + | $\qquad\quad$ ger att $\quad\displaystyle y' =4x^3 + 2 -2x^{-3} = 4x^3 + 2 - \frac{2}{x^3}\,$. |
| </ol> | </ol> | ||
| Rad 254: | Rad 255: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 4''' | + | '''Exempel 10''' |
| - | Funktionen $\,f(x)=x^2 + x^{-2}\,$ har derivatan $\displaystyle \,f'(x) = 2x^1 -2x^{-3} = 2x - \frac{2}{x^3}$. Detta betyder att | + | Funktionen $\,f(x)=x^2 + x^{-2}\,$ har derivatan |
| - | + | $$f^{\,\prime}(x) = 2x^1 -2x^{-3} = 2x - \frac{2}{x^3}\,\mbox{.}$$ | |
| - | * $\displaystyle f'(2) = 2\cdot 2 - \frac{2}{2^3}= 4- \frac{1}{4} = \frac{15}{4}$<br><br> | + | Detta betyder exempelvis att $\,f^{\,\prime}(2) = 2\cdot 2 - 2/2^3= 4- \frac{1}{4} = \frac{15}{4}\,$ och att $\,f^{\,\prime}(-1) = 2 \cdot (-1) - 2/(-1)^3 = -2 + 2 = 0\,$. Däremot är derivatan $\,f'(0)\,$ inte definierad. |
| - | * $\displaystyle f'(-1) = 2 \cdot (-1) - \frac{2}{(-1)^3} = -2 + 2 = 0$<br><br> | + | |
| - | * $ f'(0) =$ ej def. | + | |
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 5''' | + | '''Exempel 11''' |
| Ett föremål rör sig enligt $\,s(t) = t^3 -4t^2 +5t\,$, där $\,s(t)\,$ km är avståndet från startpunkten efter $\,t\,$ timmar. Beräkna $\,s'(3)\,$ och förklara vad värdet står för. | Ett föremål rör sig enligt $\,s(t) = t^3 -4t^2 +5t\,$, där $\,s(t)\,$ km är avståndet från startpunkten efter $\,t\,$ timmar. Beräkna $\,s'(3)\,$ och förklara vad värdet står för. | ||
| Rad 277: | Rad 276: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 6''' | + | '''Exempel 12''' |
| Totalkostnaden $\,T\,$ kr för tillverkning av $\,x\,$ gummidräkter ges av funktionen | Totalkostnaden $\,T\,$ kr för tillverkning av $\,x\,$ gummidräkter ges av funktionen | ||
| $$ T(x) = 40000 + 370x -0{,}09x^2 \quad \text{för} \ 0 \le x \le 200\,\mbox{.}$$ | $$ T(x) = 40000 + 370x -0{,}09x^2 \quad \text{för} \ 0 \le x \le 200\,\mbox{.}$$ | ||
| - | + | Beräkna och förklara innebörden av nedanstående uttryck. | |
| - | Beräkna och förklara | + | <br> |
| + | <br> | ||
| <ol type="a"> | <ol type="a"> | ||
| <li>$T(120)$<br><br> | <li>$T(120)$<br><br> | ||
| - | $T(120)=40000 + 370 \cdot 120 - 0{,}09 \cdot 120^2 = 83104$ <br> | + | $T(120)=40000 + 370 \cdot 120 - 0{,}09 \cdot 120^2 = 83104\,$.<br> |
| - | Totalkostnaden för att tillverka 120 gummidräkter är 83104 kr. <br><br> | + | Totalkostnaden för att tillverka 120 gummidräkter är 83104 kr.<br><br> |
| <li>$T'(120)$<br><br> | <li>$T'(120)$<br><br> | ||
| - | $T'(x)= 370 - 0{,}18x$ <br> | + | Derivatan ges av $\,T^{\,\prime}(x)= 370 - 0{,}18x\,$ och därför är $\,T^{\,\prime}(120) = 370 - 0{,}18 \cdot 120 \approx 348\,$.<br> |
| - | $T'(120) = 370 - 0{,}18 \cdot 120 \approx 348$ <br> | + | |
| Marginalkostnaden ("kostnaden för att tillverka ytterligare 1 enhet") vid 120 tillverkade gummidräkter är approximativt 348 kr.<br><br> | Marginalkostnaden ("kostnaden för att tillverka ytterligare 1 enhet") vid 120 tillverkade gummidräkter är approximativt 348 kr.<br><br> | ||
| </ol> | </ol> | ||
| Rad 300: | Rad 299: | ||
| En ''normal'' till en kurva är en rät linje som är vinkelrät mot kurvan i en viss punkt på kurvan (och därmed också vinkelrät mot kurvans tangent i denna punkt). | En ''normal'' till en kurva är en rät linje som är vinkelrät mot kurvan i en viss punkt på kurvan (och därmed också vinkelrät mot kurvans tangent i denna punkt). | ||
| - | För vinkelräta linjer gäller att produkten av deras riktningskoefficienter är $\,–1\,$, dvs. om tangentens riktningskoefficient betecknas $\,k_T\,$ och normalens $\,k_N\,$ så är $\,k_T \cdot k_N = -1\,$. Eftersom vi kan bestämma lutningen på en kurva med hjälp av derivatan så kan vi också bestämma ekvationen för en tangent eller normal om vi känner till funktionsuttrycket för kurvan. | + | För vinkelräta linjer gäller att produkten av deras riktningskoefficienter är $\,–1\,$, dvs. om tangentens riktningskoefficient betecknas $\,k_T\,$ och normalens $\,k_N\,$ så är $\,k_T \cdot k_N = -1\,$. Eftersom vi kan bestämma lutningen på en kurva med hjälp av derivatan så kan vi också bestämma ekvationen för en tangent eller en normal om vi känner till funktionsuttrycket för kurvan. |
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 7''' | + | '''Exempel 13''' |
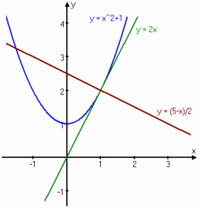
| Bestäm ekvationen för tangenten respektive normalen till kurvan $\,y=x^2 + 1\,$ i punkten $\,(1,2)\,$. | Bestäm ekvationen för tangenten respektive normalen till kurvan $\,y=x^2 + 1\,$ i punkten $\,(1,2)\,$. | ||
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning''' | + | |
| - | + | ||
| [[Bild:Normal-tangent.gif|200px|right|]] | [[Bild:Normal-tangent.gif|200px|right|]] | ||
| - | Tangentens ekvation är $\,y = kx + m\,$, där $\,k= y'(1)\,$. | + | Vi skriver tangentens ekvation som $\,y = kx + m\,$. Eftersom den ska tangera kurvan i $\,x=1\,$ har vi att $\,k= y'(1)\,$, dvs. |
| - | $y' = 2x\,,\qquad y'(1) = 2\cdot 1 = 2\,$. | + | $\qquad y' = 2x\,,\qquad y'(1) = 2\cdot 1 = 2\,$. |
| - | Eftersom linjen också passerar punkten $\,(1,2)\,$ har vi att | + | Tangentlinjen ska också passerar genom punkten $\,(1,2)\,$ och därför måste $\,(1,2)\,$ uppfylla tangentens ekvation |
| - | $2 = 2 \cdot 1 + m \quad \rightarrow \quad m = 0\,$. | + | $\qquad 2 = 2 \cdot 1 + m \quad \Leftrightarrow \quad m = 0\,$. |
| Tangentens ekvation är alltså $\,y=2x\,$. | Tangentens ekvation är alltså $\,y=2x\,$. | ||
| Rad 325: | Rad 322: | ||
| Riktningskoefficienten för normalen är $\displaystyle k_N = -\frac{1}{k_T} = -\frac{1}{2}$ . | Riktningskoefficienten för normalen är $\displaystyle k_N = -\frac{1}{k_T} = -\frac{1}{2}$ . | ||
| - | Normalen går också genom punkten $\,(1, 2)\,$ , dvs. | + | Vidare går normalen också genom punkten $\,(1, 2)\,$ , dvs. |
| - | $2= -\displaystyle \frac{1}{2}\cdot 1 + m \quad \rightarrow \quad m = \displaystyle \frac{5}{2}\,$. | + | $\qquad\displaystyle 2= -\frac{1}{2}\cdot 1 + m \quad \Leftrightarrow \quad m = \frac{5}{2}\,$. |
| - | Normalen har ekvationen $\,y= -\displaystyle \frac{x}{2} + \displaystyle \frac{5}{2} = \displaystyle \frac{5-x}{2}\,$. | + | Normalen har ekvationen $\,\displaystyle y= -\frac{x}{2} + \frac{5}{2} = \frac{5-x}{2}\,$. |
| Rad 336: | Rad 333: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 8''' | + | '''Exempel 14''' |
| - | Kurvan $\,y = 2 \, e^x - 3x\,$ har en tangent vars riktningskoefficient är $\,–1\,$. Bestäm tangeringspunkten. | + | Kurvan $\,y = 2 \, e^x - 2x\,$ har en tangent vars riktningskoefficient är $\,–1\,$. Bestäm tangeringspunkten. |
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning''' | + | Derivatan av högerledet är $\,y' = 2 \, e^x -2\,$ och i tangeringspunkten ska derivatan vara lika med $\,-1\,$, dvs. |
| - | + | $\,y' = -1\,$, och detta ger oss ekvationen | |
| - | $y' = 2 \, e^x -3$ | + | $$2 \, e^x = 2$$ |
| - | + | som har lösningen $\,x=0\,$. I punkten $\,x=0\,$ har kurvan $\,y\,$-värdet $\,y(0) = 2 \, e^0 - 2 \cdot 0 = 2\,$ och därmed är tangeringspunkiten $\,(0,2)\,$. | |
| - | $ y' = -1 \quad \rightarrow \quad 2 \, e^x = 2 \quad \rightarrow \quad x=0$ | + | |
| - | + | ||
| - | $ y(0) = 2 \, e^0 - 3 \cdot 0 = 2 $ | + | |
| - | + | ||
| - | Tangeringspunkten är $\,(0,2)\,$. | + | |
| </div> | </div> | ||