2.2. Variabelsubstitution
Sommarmatte 2
| Versionen från 17 juli 2007 kl. 14.22 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Integrationsgränser vid variabelbyte) ← Gå till föregående ändring |
Nuvarande version (17 juli 2007 kl. 14.39) (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) |
||
| (6 mellanliggande versioner visas inte.) | |||
| Rad 72: | Rad 72: | ||
| <br> | <br> | ||
| Sätt $\,u=x^3 + 1\,$. Då blir $\,u'=3x^2\,$, eller $\,du= 3x^2\, dx\,$, och | Sätt $\,u=x^3 + 1\,$. Då blir $\,u'=3x^2\,$, eller $\,du= 3x^2\, dx\,$, och | ||
| - | $$\int (x^3 + 1)^3 x^2 \, dx = \int \frac{ (x^3 + 1)^3}{3} \cdot 3x^2\, dx = \int \frac{u^3}{3}\, du = \frac{u^4}{12} + C = \frac{1}{12} (x^3 + 1)^4 + C\,\mbox{.}$$ | + | $\displaystyle\int (x^3 + 1)^3 x^2 \, dx = \int \frac{ (x^3 + 1)^3}{3} \cdot 3x^2\, dx = \int \frac{u^3}{3}\, du $<br> |
| + | $\displaystyle \phantom{\int (x^3 + 1)^3 x^2 \, dx}{}= \frac{u^4}{12} + C = \frac{1}{12} (x^3 + 1)^4 + C\,\mbox{.}$ | ||
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| Rad 81: | Rad 82: | ||
| <br> | <br> | ||
| Efter en omskrivning av $\,\tan x\,$ substituerar vi $\,u=\cos x\,$ | Efter en omskrivning av $\,\tan x\,$ substituerar vi $\,u=\cos x\,$ | ||
| - | $$\int \tan x \, dx = \int \frac{\sin x}{\cos x} \, dx = \left[\,\eqalign{u&= \cos x\cr u' &= - \sin x\cr du&= - \sin x \, dx}\,\right] = \int -\frac{1}{u}\, du = - \ln |u| +C = -\ln |\cos x| + C\,\mbox{.}$$ | + | $\displaystyle \int \tan x \, dx = \int \frac{\sin x}{\cos x} \, dx = \left[\,\eqalign{u&= \cos x\cr u' &= - \sin x\cr du&= - \sin x \, dx}\,\right] $<br><br> |
| + | $\displaystyle \phantom{\int \tan x \, dx}{}= \int -\frac{1}{u}\, du = - \ln |u| +C = -\ln |\cos x| + C\,\mbox{.}$ | ||
| </div> | </div> | ||
| Rad 105: | Rad 107: | ||
| Sätt $\,u=e^x\,$ vilket ger att $\,u'= e^x\,$ och $\,du= e^x\, dx\,$. Integrationsgränsen $\,x=0\,$ motsvaras då av $\,u=e^0 = 1\,$ och $\,x=2\,$ motsvaras av $\,u=e^2\,$ | Sätt $\,u=e^x\,$ vilket ger att $\,u'= e^x\,$ och $\,du= e^x\, dx\,$. Integrationsgränsen $\,x=0\,$ motsvaras då av $\,u=e^0 = 1\,$ och $\,x=2\,$ motsvaras av $\,u=e^2\,$ | ||
| - | $$\int_{0}^{2} \frac{e^x}{1 + e^x} \, dx = \int_{1}^{\,e^2} \frac{1}{1 + u} \, du = \Bigl[\,\ln |1+ u |\,\Bigr]_{1}^{e^2} = \ln (1+ e^2) - \ln 2 = \ln\frac{1+ e^2}{2}\,\mbox{.}$$ | + | $$\int_{0}^{2} \frac{e^x\, dx}{1 + e^x} = \int_{1}^{\,e^2} \frac{du}{1 + u} = \Bigl[\,\ln |1+ u |\,\Bigr]_{1}^{e^2} = \ln (1+ e^2) - \ln 2 = \ln\frac{1+ e^2}{2}\,\mbox{.}$$ |
| + | </div> | ||
| + | |||
| + | |||
| - | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
| - | |||
| [[Bild:Integral20.gif|200px|right]] | [[Bild:Integral20.gif|200px|right]] | ||
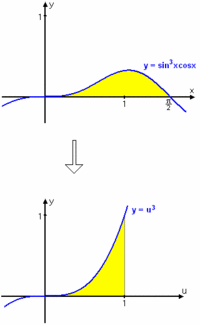
| Beräkna integralen $ \ \displaystyle \int_{0}^{\pi/2} \sin^3 x \cos x \, dx\,$. | Beräkna integralen $ \ \displaystyle \int_{0}^{\pi/2} \sin^3 x \cos x \, dx\,$. | ||
| Rad 121: | Rad 124: | ||
| Substitutionen $\,u=\sin x\,$ ger att $\,du=\cos x\,dx\,$ och integrationsgränserna förändras till $\,u=\sin 0=0\,$ och $\,u=\sin(\pi/2)=1\,$. Integralen blir | Substitutionen $\,u=\sin x\,$ ger att $\,du=\cos x\,dx\,$ och integrationsgränserna förändras till $\,u=\sin 0=0\,$ och $\,u=\sin(\pi/2)=1\,$. Integralen blir | ||
| $$\int_{0}^{\pi/2} \sin^3 x\,\cos x \, dx= \int_{0}^{1} u^3\,du = \Bigl[ {\textstyle\frac{1}{4}}u^4\,\Bigr]_{0}^{1} = {\textstyle\frac{1}{4}} - 0 = {\textstyle\frac{1}{4}}\,\mbox{.}$$ | $$\int_{0}^{\pi/2} \sin^3 x\,\cos x \, dx= \int_{0}^{1} u^3\,du = \Bigl[ {\textstyle\frac{1}{4}}u^4\,\Bigr]_{0}^{1} = {\textstyle\frac{1}{4}} - 0 = {\textstyle\frac{1}{4}}\,\mbox{.}$$ | ||
| - | |||
| - | |||
| (Figuren till höger visar vad som händer vid variabelbytet; integrand och variabel ändras. Integralens värde, storleken på arean, ändras dock inte.) | (Figuren till höger visar vad som händer vid variabelbytet; integrand och variabel ändras. Integralens värde, storleken på arean, ändras dock inte.) | ||
| Rad 132: | Rad 133: | ||
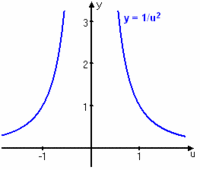
| Betrakta beräkningen | Betrakta beräkningen | ||
| - | $$\int_{-\pi/2}^{\pi/2} \frac{ \cos x} {\sin^2 x}\, dx = \left[\,\eqalign{ &u = \sin x\cr &du = \cos x \, dx\cr &u(-\pi/2) = -1\cr &u (\pi/2) = 1}\,\right ] = \int_{-1}^{1} \frac{1}{u^2} \, du = \Bigl[\, -\frac{1}{u}\, \Bigr]_{0}^{1} = -1 - 1 = -2\,\mbox{.}$$ | + | $$\int_{-\pi/2}^{\pi/2} \frac{ \cos x} {\sin^2 x}\, dx = \left[\,\eqalign{ &u = \sin x\cr &du = \cos x \, dx\cr &u(-\pi/2) = -1\cr &u (\pi/2) = 1}\,\right ] = \int_{-1}^{1} \frac{du}{u^2} = \Bigl[\, \frac{-1}{u}\, \Bigr]_{-1}^{1} = -1 - 1 = -2\,\mbox{.}$$ |
| [[Bild:Integral21.gif|200px|right]] | [[Bild:Integral21.gif|200px|right]] | ||
| Rad 140: | Rad 141: | ||
| + | </div> | ||
| - | + | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | |
| - | + | ||
| - | + | ||
| - | </div> | + | |
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
[redigera] VariabelsubstitutionNär man inte direkt kan bestämma en primitiv funktion genom att utnyttja de vanliga deriveringsreglerna ”baklänges”, behöver man andra metoder eller tekniker. En sådan är variabelsubstitution, vilken kan sägas baseras på regeln för derivering av sammansatta funktioner — den s.k. kedjeregeln. Kedjeregeln $\ \displaystyle \frac{d}{dx}\,f(u(x)) = f^{\,\prime} (u(x)) \cdot u'(x)\ \ $ kan i integralform skrivas $$ \displaystyle \int f^{\,\prime}(u(x)) \cdot u'(x) \, dx = f(u(x)) + C$$ eller, $$ \displaystyle \int f(u(x)) \cdot u'(x) \, dx = F (u(x)) + C\,\mbox{,}$$ där $\,F\,$ är en primitiv funktion till $\,f\,$. Jämför vi denna formel med $$ \displaystyle \int f(u) \, du = F(u) + C\,\mbox{,}$$ så kan vi se det som att vi ersätter uttrycket $\,u(x)\,$ med variabeln $\,u\,$ och $\,u'(x)\, dx\,$ med $\,du\,$. Man kan alltså omvandla den krångligare integranden $\,f(u(x)) \cdot u'(x)\,$ (med $\,x\,$ som variabel) med den förhoppningsvis enklare $\,f(u)\,$ (med $\,u\,$ som variabel). Metoden kallas variabelsubstitution och kan användas när integranden kan skrivas på formen $\,f(u(x)) \cdot u'(x)\,$. Anm.1 Anm.2 $$\lim_{\Delta x \to 0} \displaystyle \frac{\Delta u}{\Delta x} = \displaystyle \frac{du}{dx} = u'(x)\,\mbox{,}$$ vilket när $\,\Delta x\,$ går mot noll kan betraktas som en formell gränsövergång $$\Delta u \approx u'(x) \Delta x \quad \to \quad du = u'(x) \, dx\,\mbox{,}$$ dvs., en liten ändring, $\,dx\,$, i variabeln $\,x\,$ ger upphov till en ungefärlig ändring $\,u'(x)\,dx\,$ i variabeln $\,u\,$. Exempel 1 Bestäm integralen $ \displaystyle\ \int 2 x\, e^{x^2} \, dx$.
Exempel 2 Bestäm integralen $\ \displaystyle \int (x^3 + 1)^3 \cdot x^2 \, dx\,$.
Exempel 3 Bestäm integralen $\ \displaystyle \int \tan x \, dx\ \ $ där $\,-\pi/2 < x < \pi/2\,$.
[redigera] Integrationsgränser vid variabelbyteVid beräkning av bestämda integraler, t.ex. en area, där man använder variabelsubstitution kan man gå till väga på två sätt. Antingen beräknar man integralen som vanligt, byter tillbaka till den ursprungliga variabeln och sätter in de ursprungliga integrationsgränserna. Alternativt ändrar man integrationsgränser samtidigt som man gör variabelbytet. De båda metoderna illustreras i följande exempel. Exempel 4 Beräkna integralen $\ \displaystyle \int_{0}^{2} \displaystyle \frac{e^x}{1 + e^x} \, dx$. Metod 1 Sätt $\,u=e^x\,$ vilket ger att $\,u'= e^x\,$ och $\,du= e^x\,dx$ $$\eqalign{\int_{0}^{2} \frac{e^x}{1 + e^x} \, dx &= \int_{x=0}^{\,x=2} \frac{1}{1 + u} \, du = \Bigl[\,\ln |1+ u |\,\Bigr]_{x=0}^{x=2} = \Bigl[\,\ln (1+ e^x)\,\Bigr]_{0}^{2}\cr &= \ln (1+ e^2) - \ln 2 = \ln \frac{1+ e^2}{2}\,\mbox {.}}$$ Observera att integrationsgränserna måste skrivas $\,x = 0\,$ och $\,x = 2\,$ när integrationsvariabeln inte är $\,x\,$. Det vore fel att skriva $$\int_{0}^{2} \frac{e^x}{1 + e^x} \, dx = \int_{0}^{2} \frac{1}{1 + u} \, du \quad \text{ osv.}$$ Metod 2 Sätt $\,u=e^x\,$ vilket ger att $\,u'= e^x\,$ och $\,du= e^x\, dx\,$. Integrationsgränsen $\,x=0\,$ motsvaras då av $\,u=e^0 = 1\,$ och $\,x=2\,$ motsvaras av $\,u=e^2\,$ $$\int_{0}^{2} \frac{e^x\, dx}{1 + e^x} = \int_{1}^{\,e^2} \frac{du}{1 + u} = \Bigl[\,\ln |1+ u |\,\Bigr]_{1}^{e^2} = \ln (1+ e^2) - \ln 2 = \ln\frac{1+ e^2}{2}\,\mbox{.}$$
Exempel 5 Beräkna integralen $ \ \displaystyle \int_{0}^{\pi/2} \sin^3 x \cos x \, dx\,$.
(Figuren till höger visar vad som händer vid variabelbytet; integrand och variabel ändras. Integralens värde, storleken på arean, ändras dock inte.) Exempel 6 Betrakta beräkningen $$\int_{-\pi/2}^{\pi/2} \frac{ \cos x} {\sin^2 x}\, dx = \left[\,\eqalign{ &u = \sin x\cr &du = \cos x \, dx\cr &u(-\pi/2) = -1\cr &u (\pi/2) = 1}\,\right ] = \int_{-1}^{1} \frac{du}{u^2} = \Bigl[\, \frac{-1}{u}\, \Bigr]_{-1}^{1} = -1 - 1 = -2\,\mbox{.}$$ Denna uträkning är dock felaktig, vilket beror på att $\,f(u)=1/u^2\,$ inte är kontinuerlig i hela intervallet $\,[-1,1]\,$. Villkoret att $\,f(u(x))\,$ ska vara definierad och kontinuerlig för alla värden som $u(x)$ kan anta i det aktuella intervallet behövs om man vill vara säker på att substitutionen $\,u=u(x)\,$ ska fungera.
|