1.3 Max- och minproblem
Sommarmatte 2
| Versionen från 14 juni 2007 kl. 14.43 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) ← Gå till föregående ändring |
Nuvarande version (4 juli 2007 kl. 14.05) (redigera) (ogör) KTH.SE:u1rp004j (Diskussion | bidrag) (→Teckentabell) |
||
| (5 mellanliggande versioner visas inte.) | |||
| Rad 107: | Rad 107: | ||
| ==Kritiska punkter== | ==Kritiska punkter== | ||
| Punkter där $\,f^{\,\prime}(x) = 0\,$ kallas kritiska (eller stationära) punkter och är vanligtvis av tre olika slag: | Punkter där $\,f^{\,\prime}(x) = 0\,$ kallas kritiska (eller stationära) punkter och är vanligtvis av tre olika slag: | ||
| - | * lokal maximipunkt med $f^{\,\prime}(x) > 0 $ till vänster, och $f^{\,\prime}(x) < 0 $ till höger om punkten. | + | * lokal maximipunkt med $\,f^{\,\prime}(x) > 0\,$ till vänster, och $\,f^{\,\prime}(x) < 0\,$ till höger om punkten. |
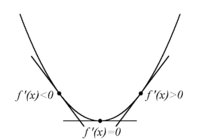
| - | * lokal minimipunkt med $f^{\,\prime}(x) < 0 $ till vänster, och $f^{\,\prime}(x) > 0 $ till höger om punkten. | + | * lokal minimipunkt med $\,f^{\,\prime}(x) < 0\,$ till vänster, och $\,f^{\,\prime}(x) > 0\,$ till höger om punkten. |
| - | * terrasspunkt med $f^{\,\prime}(x) < 0 $ eller $f^{\,\prime}(x) > 0 $ på båda sidor om punkten. | + | * terrasspunkt med $\,f^{\,\prime}(x) < 0\,$ eller $\,f^{\,\prime}(x) > 0\,$ på båda sidor om punkten. |
| + | Observera att en punkt kan vara en lokal maximi-/minimipunkt utan att $\,f^{\,\prime}(x) = 0\,$; läs mer i avsnittet om ''[[#Max- och minpunkter (extrempunkter)|max- och minpunkter]]''. | ||
| [[Bild:Mamiter2.gif|400px|center|]] | [[Bild:Mamiter2.gif|400px|center|]] | ||
| Rad 141: | Rad 142: | ||
| |width="50px" align="center"| $x-2$ | |width="50px" align="center"| $x-2$ | ||
| |width="50px" align="center"| $-$ | |width="50px" align="center"| $-$ | ||
| + | |width="50px" align="center"| $-$ | ||
| + | |width="50px" align="center"| $-$ | ||
| |width="50px" align="center"| $0$ | |width="50px" align="center"| $0$ | ||
| - | |width="50px" align="center"| $+$ | ||
| - | |width="50px" align="center"| $+$ | ||
| |width="50px" align="center"| $+$ | |width="50px" align="center"| $+$ | ||
| |- | |- | ||
| |width="50px" align="center"| $x+2$ | |width="50px" align="center"| $x+2$ | ||
| |width="50px" align="center"| $-$ | |width="50px" align="center"| $-$ | ||
| - | |width="50px" align="center"| $-$ | ||
| - | |width="50px" align="center"| $-$ | ||
| |width="50px" align="center"| $0$ | |width="50px" align="center"| $0$ | ||
| + | |width="50px" align="center"| $+$ | ||
| + | |width="50px" align="center"| $+$ | ||
| |width="50px" align="center"| $+$ | |width="50px" align="center"| $+$ | ||
| |- | |- | ||
| Rad 230: | Rad 231: | ||
| Funktionens derivata ges av | Funktionens derivata ges av | ||
| $$y' = 12x^3 + 12x^2 - 24x = 12x(x^2+x-2)\,\mbox{.}$$ | $$y' = 12x^3 + 12x^2 - 24x = 12x(x^2+x-2)\,\mbox{.}$$ | ||
| - | För att bestämma hur derivatans tecken varierar över tallinjen försöker vi faktorisera derivatan så långt som möjligt. Vi har redan lyckats bryta ut faktorn $\,12x\,$ och vi kan faktorisera deluttrycket $\,x^2+x-2\,$ ytterligare genom att hitta nollställena till detta deluttrycket, dvs. | + | För att bestämma hur derivatans tecken varierar över tallinjen försöker vi faktorisera derivatan så långt som möjligt. Vi har redan lyckats bryta ut faktorn $\,12x\,$ och vi kan faktorisera det återstående uttrycket $\,x^2+x-2\,$ ytterligare genom att hitta dess nollställen |
| $$x^2+x-2=0\qquad\Leftrightarrow\qquad x=-2\quad\text{eller}\quad x=1.$$ | $$x^2+x-2=0\qquad\Leftrightarrow\qquad x=-2\quad\text{eller}\quad x=1.$$ | ||
| Detta betyder att $\,x^2+x-2=(x+2)(x-1)\,$ och hela derivatan kan skrivas som | Detta betyder att $\,x^2+x-2=(x+2)(x-1)\,$ och hela derivatan kan skrivas som | ||
| $$y' = 12x(x+2)(x-1)\,\mbox{.}$$ | $$y' = 12x(x+2)(x-1)\,\mbox{.}$$ | ||
| - | De enskilda faktorerna har tecken som framgår av tabellen nedan | + | Det går direkt ur denna formel se att derivatan är noll för $\,x=-2\,$, $\,x=0\,$ och $\,x=1\,$. Dessutom kan vi se hur derivatans tecken varierar genom att undersöka tecknet för varje enskild faktor i produkten för olika värden på $\,x\,$ |
| {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | ||
| Rad 276: | Rad 277: | ||
| |} | |} | ||
| - | Genom att derivatan är produkten av dessa faktorer får vi fram derivatans tecken i intervallen mellan de kritiska punkterna. | + | Derivatan är produkten av dessa faktorer och vi får derivatans tecken genom att multiplicera ihop faktorernas tecken i respektive intervall. |
| {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | ||
| Rad 319: | Rad 320: | ||
| <br> | <br> | ||
| <br> | <br> | ||
| - | Derivatan ges av | + | Derivatan till funktionen ges av |
| - | $$y' = 1 - \displaystyle \frac{2}{3} x^{-\frac{1}{3}} = 1- \displaystyle \frac {2}{3} \cdot \frac{1}{\sqrt[3]{x}}\,\mbox{.}$$ | + | $$y' = 1 - \frac{2}{3} x^{-1/3} = 1- \frac {2}{3} \cdot \frac{1}{\sqrt[\scriptstyle 3]{x}}\,\mbox{.}$$ |
| - | Från detta uttryck ser vi att $\,y'\,$ är alltså inte definierad för $\,x = 0\,$ (vilket dock $\,y\,$ är). | + | Från detta uttryck ser vi att $\,y'\,$ inte är definierad för $\,x = 0\,$ (vilket dock $\,y\,$ är). Detta betyder att funktionen har en singulär punkt i $\,x=0\,$. |
| De kritiska punkterna till funktionen ges av | De kritiska punkterna till funktionen ges av | ||
| - | $$\displaystyle y'=0 \quad \Leftrightarrow \quad 1= \frac {2}{3} \cdot \frac{1}{\sqrt[3]{x}}\quad\Leftrightarrow\quad \sqrt[3]{x} = {\textstyle\frac {2}{3}} \quad \Leftrightarrow \quad x = \bigl({\textstyle\frac{2}{3}}\bigr)^3 = \frac{8}{27}\,\mbox{.}$$ | + | $$\displaystyle y'=0 \quad \Leftrightarrow \quad 1= \frac {2}{3} \cdot \frac{1}{\sqrt[3]{x}}\quad\Leftrightarrow\quad \sqrt[3]{x} = {\textstyle\frac {2}{3}} \quad \Leftrightarrow \quad x = \bigl({\textstyle\frac{2}{3}}\bigr)^3 = {\textstyle\frac{8}{27}}\,\mbox{.}$$ |
| - | + | De enda punkter där funktionen eventuellt kan ha extrempunkter är alltså $\,x=0\,$ och $\,x=\frac{8}{27}\,$. För att avgöra dessa punkters karaktär skriver vi upp en teckentabell: | |
| - | Teckentabell: | + | |
| {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | ||
| |- | |- | ||
| - | |width= "50" ALIGN="center"| $x$ | + | |width="50px" align="center" style="background:#efefef;"| $x$ |
| - | | | + | |width="50px" align="center" style="background:#efefef;"| |
| - | |ALIGN="center"| $0$ | + | |width="50px" align="center" style="background:#efefef;"| $0$ |
| - | | | + | |width="50px" align="center" style="background:#efefef;"| |
| - | |ALIGN="center"| $\frac{8}{27}$ | + | |width="50px" align="center" style="background:#efefef;"| $\frac{8}{27}$ |
| - | | | + | |width="50px" align="center" style="background:#efefef;"| |
| |- | |- | ||
| - | |width= "50" ALIGN="center"| $y'$ | + | |width="50px" align="center"| $y'$ |
| - | |width= "50" ALIGN="center"| $+$ | + | |width="50px" align="center"| $+$ |
| - | |width= "50" ALIGN="center"| $ ej def.$ | + | |width="50px" align="center"| ej def. |
| - | |width= "50" ALIGN="center"| $-$ | + | |width="50px" align="center"| $-$ |
| - | |width= "50" ALIGN="center"| $0$ | + | |width="50px" align="center"| $0$ |
| - | |width= "50" ALIGN="center"| $+$ | + | |width="50px" align="center"| $+$ |
| |- | |- | ||
| - | |ALIGN="center"| $y$ | + | |width="50px" align="center"| $y$ |
| - | |ALIGN="center"|$\nearrow$ | + | |width="50px" align="center"| $\nearrow$ |
| - | |ALIGN="center"| | + | |width="50px" align="center"| $0$ |
| - | |ALIGN="center"| $\searrow$ | + | |width="50px" align="center"| $\searrow$ |
| - | |ALIGN="center"| $\rightarrow$ | + | |width="50px" align="center"| $-\frac{4}{27}$ |
| - | |ALIGN="center"| $\nearrow$ | + | |width="50px" align="center"| $\nearrow$ |
| - | |} | + | |
| - | + | ||
| - | + | ||
| - | {| | + | |
| - | |- | + | |
| - | | width=45% valign=top | | + | |
| - | $y(0)=0$ | + | |
| - | + | ||
| - | $y(\frac{8}{27}) = -\frac{4}{27}$ | + | |
| - | | width=50% valign=top | | + | |
| - | [[Bild:X-xu23.gif|200px|right|]] | + | |
| - | | width=5% valign=top | | + | |
| - | + | ||
| |} | |} | ||
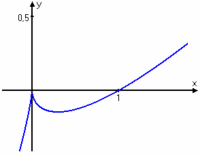
| + | Kurvan har alltså en lokal maximipunkt i $\,(0, 0)\,$ (en spets) och en lokal minimipunkt i $\,(\frac{8}{27},-\frac{4}{27})\,$. | ||
| - | Kurvan har alltså en max-punkt i $(0, 0)$ (en spets) och en min-punkt i $( \frac{8}{27} , -\frac{4}{27})$. | + | [[Bild:X-xu23.gif|200px|center|]] |
| </div> | </div> | ||
| Rad 395: | Rad 383: | ||
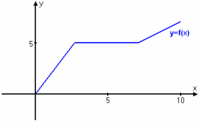
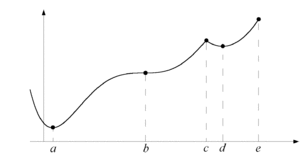
| Funktionen ovan betraktas endast i intervallet $a\le x \le e$. | Funktionen ovan betraktas endast i intervallet $a\le x \le e$. | ||
| - | Vi ser att funktionens minsta värde i detta intervall inträffar i $x=b$ , medan största värdet återfinns i ändpunkten $x=e$. | + | Vi ser att funktionens minsta värde i detta intervall inträffar i den kritiska punkten $x=b$ , medan största värdet återfinns i ändpunkten $x=e$. |
| Rad 401: | Rad 389: | ||
| '''Exempel 7''' | '''Exempel 7''' | ||
| - | Bestäm största och minsta värde för funktionen $f(x) = x^3 -3x + 2$ i intervallet $-0{,}5 \le x \le 1$. | + | Bestäm största och minsta värde för funktionen $\,f(x) = x^3 -3x + 2\,$ i intervallet $\,-0{,}5 \le x \le 1\,$. |
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning''' | + | Vi deriverar funktionen $\,f^{\,\prime}(x) = 3x^2 -3\,$ och sätter derivatan lika med noll för att få fram alla kritiska punkter |
| - | + | $$f^{\,\prime}(x) = 0 \quad \Leftrightarrow \quad x^2 = 1 \quad \Leftrightarrow \quad x= \pm 1\,\mbox{.}$$ | |
| - | $f'(x) = 3x^2 -3$ | + | Punkten $x = –1$ ligger dock utanför den aktuella definitionsmängden och $x = 1$ sammanfaller med definitionsmängdens ena ändpunkt. Eftersom funktionen saknar singulära punkten (funktioen är deriverbar överallt) måste funktionens största och minsta värde antas i intervallets ändpunkter. |
| - | + | $$\eqalign{f(-0{,}5) &= 3{,}375\cr f(1)&=0}$$ | |
| - | $f'(x) = 0 \quad \rightarrow \quad x^2 = 1 \quad \rightarrow \quad x= \pm 1 $ | + | |
| - | + | ||
| - | + | ||
| - | $x = –1$ ligger dock utanför den aktuella definitionsmängden och $x = 1$ sammanfaller med definitionsmängdens ena ändpunkt, varför största och minsta värde för $f(x)$ måste finnas i intervallets ändpunkter. | + | |
| - | + | ||
| - | + | ||
| - | $f(-0{,}5) = 3{,}375$ | + | |
| - | + | ||
| - | $f(1)=0$ | + | |
| - | + | ||
| - | + | ||
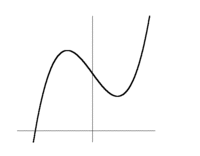
| Funktionens största värde i det givna intervallet är alltså $3{,}375$. Minsta värdet är $0$ (se fig.) | Funktionens största värde i det givna intervallet är alltså $3{,}375$. Minsta värdet är $0$ (se fig.) | ||
| Rad 428: | Rad 405: | ||
| ==Andraderivatan== | ==Andraderivatan== | ||
| - | Tecknet på derivatan av en funktion ger oss information om huruvida funktionen är växande eller avtagande. På samma sätt kan andraderivatans tecken visa om förstaderivatan är växande eller avtagande. Detta kan man bl.a. utnyttja för att ta reda på om en given extrempunkt är en max-, eller min-punkt. | + | Tecknet på derivatan av en funktion ger oss information om huruvida funktionen är växande eller avtagande. På samma sätt kan andraderivatans tecken visa om förstaderivatan är växande eller avtagande. Detta kan man bl.a. utnyttja för att ta reda på om en given extrempunkt är en max-, eller minpunkt. |
| - | Om $f(x)$ har en max-punkt, där $f'(x)=0$ : | ||
| - | {| | ||
| - | |- | ||
| - | | width=50% valign=top | | ||
| - | {| class="wikitable" cellpadding="4px" cellspacing="0px" width="100%" | ||
| - | |- | ||
| - | |width="30" style="text-align:right;"| $\rightarrow$ | ||
| - | |style="text-align:left" | kurvans lutning, $f'(x)$ , är avtagande | ||
| - | |- | ||
| - | | | ||
| - | |(från positiv lutning till negativ lutning) | ||
| - | |- | ||
| - | |width="30" style="text-align:right;"| $\rightarrow$ | ||
| - | |style="text-align:left" | derivatan av $f'(x)$ är negativ | ||
| - | |- | ||
| - | |width="30" style="text-align:right;"| $\rightarrow$ | ||
| - | |style="text-align:left" | $f{'}{'}(x) < 0$ | ||
| - | |} | ||
| - | | width=45% valign=top | | ||
| - | [[Bild:Fmax.gif|200px]] | ||
| - | | width=5% valign=top | | ||
| - | |} | ||
| - | Om $f(x)$ har en min-punkt, där $f'(x)= 0$: | + | [[Bild:Fmax.gif|200px|right]] |
| - | {| | + | Om funktionen $\,f(x)\,$ har en kritisk punkt i $\,x=a\,$ där $f^{\,\prime\prime}(a)<0$, då gäller att |
| - | |- | + | :# Derivatan $\,f^{\,\prime}(x)\,$ är strängt avtagande i en omgivning kring $\,x=a\,$. |
| - | | width=50% valign=top | | + | :# Eftersom $\,f^{\,\prime}(a)=0\,$ är alltså $\,f^{\,\prime}(x)>0\,$ till vänster om $\,x=a\,$ och $\,f^{\,\prime}(x)<0\,$ till höger om $\,x=a\,$. |
| - | {| class="wikitable" cellpadding="4px" cellspacing="0px" width="100%" | + | :# Detta medför att funktionen $\,f(x)\,$ har en lokal maximipunkt i $\,x=a\,$. |
| - | |- | + | |
| - | |width="30" style="text-align:right;"| $\rightarrow$ | + | |
| - | |style="text-align:left" | kurvans lutning, $f'(x)$, är växande | + | |
| - | |- | + | |
| - | | | + | |
| - | |(från negativ lutning till positiv lutning) | + | |
| - | |- | + | |
| - | |width="30" style="text-align:right;"| $\rightarrow$ | + | |
| - | |style="text-align:left" | derivatan av $f'(x)$ är positiv | + | |
| - | |- | + | |
| - | |width="30" style="text-align:right;"| $\rightarrow$ | + | |
| - | |style="text-align:left" | $f{'}{'}(x) > 0$ | + | |
| - | |} | + | |
| - | | width=45% valign=top | | + | |
| - | [[Bild:Fmin.gif|200px]] | + | |
| - | | width=5% valign=top | | + | |
| - | |} | + | |
| - | Om $f{'}{'}(x)=0$, får vi ingen information utan ytterligare undersökning krävs, t.ex. teckentabell. | ||
| + | [[Bild:Fmin.gif|200px|right]] | ||
| + | Om funktionen $\,f(x)\,$ har en kritisk punkt i $\,x=a\,$ där $f^{\,\prime\prime}(a)>0$, då gäller att | ||
| + | :# Derivatan $\,f^{\,\prime}(x)\,$ är strängt växande i en omgivning kring $\,x=a\,$. | ||
| + | :# Eftersom $\,f^{\,\prime}(a)=0\,$ är alltså $\,f^{\,\prime}(x)<0\,$ till vänster om $\,x=a\,$ och $\,f^{\,\prime}(x)>0\,$ till höger om $\,x=a\,$. | ||
| + | :# Detta medför att funktionen $\,f(x)\,$ har en lokal minimipunkt i $\,x=a\,$. | ||
| - | <div class="exempel"> | ||
| - | '''Exempel 8''' | ||
| - | Bestäm alla extrempunkter för funktionen $f(x)=x^3 -x^2 -x +2$ och bestäm deras karaktär med hjälp av andraderivatan. | + | Om $\,f^{\,\prime\prime}(a)=0$, får vi ingen information utan ytterligare undersökning krävs, t.ex. teckentabell. |
| - | '''Lösning''' | + | <div class="exempel"> |
| + | '''Exempel 8''' | ||
| - | $f'(x) = 3x^2 -2x - 1$ | + | Bestäm alla extrempunkter för funktionen $\,f(x)=x^3 -x^2 -x +2\,$ och bestäm deras karaktär med hjälp av andraderivatan. |
| - | + | <br> | |
| - | $f'(x) = 0 \quad \rightarrow \quad x^2 - \displaystyle \frac{2}{3} x - \frac{1}{3} = 0 \quad \rightarrow \quad x=1 \quad eller \quad x = -\displaystyle \frac{1}{3}$ | + | <br> |
| - | + | Funktionen är ett polynom och är därför deriverbar överallt. Om funktionen har några extrempunkter så måste de därför finnas bland de kritiska punkterna. Vi deriverar därmed funktionen, $\,f^{\,\prime}(x) = 3x^2 -2x - 1\,$, och sätter derivatan lika med noll | |
| - | $f(x)$ har extrempunkter då $x = 1$ och $x=-\displaystyle \frac{1}{3}$. | + | $$f^{\,\prime}(x) = 0 \quad \Leftrightarrow \quad x^2 - \frac{2}{3} x - \frac{1}{3} = 0 \quad \Leftrightarrow \quad x=1 \quad\text{eller}\quad x = -\frac{1}{3}\,\mbox{.}$$ |
| - | + | Funktionen har kritiska punkter i $x = 1$ och $x=-\frac{1}{3}$. Med hjälp av tecknet på andraderivatan $\,f^{\,\prime\prime}(x)=6x-2\,$ kan vi bestämma vilken typ av extrempunkt respektive kritisk punkt är. | |
| - | + | :*För $\,x=-\frac{1}{3}\,$ har vi att $\,f^{\,\prime\prime}(-\frac{1}{3})=-4<0\,$ och det betyder att $\,x=-\frac{1}{3}\,$ är en lokal maximipunkt. | |
| - | Andraderivatans tecken ger vilken typ: | + | :*För $\,x=1\,$ har vi att $\,f^{\,\prime\prime}(1)=4>0\,$ och det betyder att $\,x=1\,$ är en lokal minimipunkt. |
| - | + | ||
| - | $f{'}{'}(x) = 6x - 2$ | + | |
| - | + | ||
| - | $f{'}{'}(-\displaystyle \frac{1}{3}) = -4 < 0 \quad \rightarrow \quad f_{max} \mbox{ då} x = -\displaystyle \frac{1}{3}$. | + | |
| - | + | ||
| - | $f{'}{'}(1) = 4 > 0 \quad \rightarrow \quad f_{min} \mbox{ då} x = 1$. | + | |
| </div> | </div> | ||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[redigera] Växande och avtagandeBegreppen växande och avtagande känns kanske självklara när man pratar om matematiska funktioner; om funktionen är växande så lutar grafen uppåt och den är avtagande så lutar grafen nedåt. De matematiska definitionerna är följande: En funktion är växande i ett intervall om för alla $\,x\,$ inom intervallet gäller att $$x_1 < x_2\quad\Rightarrow\quad f(x_1) \le f(x_2)\,\mbox{.}$$ En funktion är avtagande i ett intervall om för alla $x$ inom intervallet gäller att $$x_1 < x_2\quad\Rightarrow\quad f(x_1) \ge f(x_2)\,\mbox{.}$$ Med vardagligt språk säger alltså definitionen av t.ex. växande funktion att för ett x-värde till höger på x-axeln är funktionsvärdet minst lika stort som för ett x-värde till vänster. Lägg märke till att denna definition innebär att en funktion kan vara konstant i ett intervall och ändå vara växande eller avtagande. En funktion som är konstant i hela det aktuella intervallet är enligt definitionen både växande och avtagande.
En funktion är strängt växande i ett intervall om för alla $\,x\,$ inom intervallet gäller att $$x_1 < x_2\quad\Rightarrow\quad f(x_1) < f(x_2)\,\mbox{.}$$ En funktion är strängt avtagande i ett intervall om för alla $x$ inom intervallet gäller att $$x_1 < x_2\quad\Rightarrow\quad f(x_1) > f(x_2)\,\mbox{.}$$ (En strängt växande/avtagande funktion får alltså inte vara konstant i någon del av intervallet.) Exempel 1
Derivatan kan givetvis användas för att undersöka om en funktion är växande eller avtagande. Vi har att $$\eqalign{f^{\,\prime}(x) > 0 \quad&\Rightarrow \quad f(x) \text{ är (strängt) växande.}\cr f^{\,\prime}(x) < 0 \quad&\Rightarrow \quad f(x) \text{ är (strängt) avtagande.}}$$
[redigera] Kritiska punkterPunkter där $\,f^{\,\prime}(x) = 0\,$ kallas kritiska (eller stationära) punkter och är vanligtvis av tre olika slag:
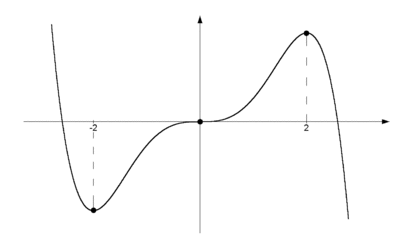
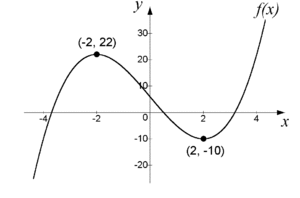
Observera att en punkt kan vara en lokal maximi-/minimipunkt utan att $\,f^{\,\prime}(x) = 0\,$; läs mer i avsnittet om max- och minpunkter. Funktionen i figuren ovan har en lokal minimipunkt för $\,x = -2\,$, terrasspunkt för $\,x = 0\,$ och lokal maximipunkt för $\,x = 2\,$. [redigera] TeckentabellGenom att studera derivatans tecken (+, – eller 0) kan vi alltså få en bra uppfattning om kurvans utseende. Detta utnyttjar man i en s.k. teckentabell. Man bestämmer först de x-värden där $\,f^{\,\prime}(x) =0\,$ och beräknar sedan derivatans tecken på båda sidor om dessa. Med hjälp av en eller annan "stödpunkt" på kurvan kan man dessutom utifrån teckentabellen skissera kurvan på ett ofta godtagbart sätt. Exempel 2 Gör en teckentabell över funktionen $\,f(x) = x^3 -12x + 6\,$ och skissera därefter funktionens graf.
Eftersom derivatan är produkten av $\,x-2\,$ och $\,x+2\,$ så kan vi bestämma derivatans tecken utifrån faktorernas tecken och ställa upp en följande tabell över derivatans tecken på tallinjen:
I tabellens sista rad har vi skrivit ut pilar som visar om funktionen är strängt växande $\,(\,\nearrow\,\,)\,$ eller strängt avtagande $\,(\,\searrow\,\,)\,$ i respektive intervall samt funktionens värde i de kritiska punkterna $\,x=-2\,$ och $\,x=2\,$. Från diagrammet ser vi att $\,f(x)\,$ har en lokal maximipunkt i $\,(–2, 22)\,$ och en lokal minimipunkt i $\,(2, –10)\,$. Grafen kan nu skissas:
[redigera] Max- och minpunkter (extrempunkter)Punkter där en funktion antar sitt största eller minsta värde i jämförelse med omgivningen kallas för lokala maximi- eller minimipunkter (förkortas ofta max- och minpunkter). Med ett gemensamt namn kallas dessa punkter för extrempunkter. En extrempunkt kan uppträda i tre olika slags punkter:
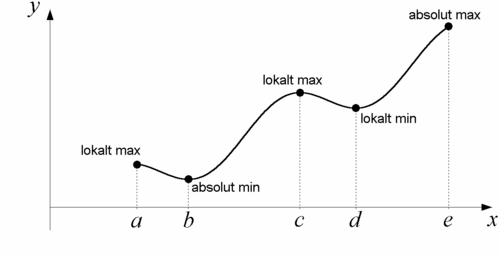
Exempel 3 Funktionen nedan har fyra extrempunkter; maxpunkter i $\,x=c\,$ och $\,x=e\,$, och minpunkter i $\,x=a\,$ och $\,x=d\,$. I $\,x=a\,$, $\,x=b\,$ och $\,x=d\,$ är $\,f'(x) =0\,$, men det är endast i $\,x=a\,$ och $\,x=d\,$ som vi har extrempunkter, eftersom $\,x=b\,$ är en terrasspunkt. I $\,x=c\,$ är inte derivatan definierad (eftersom det är en spets, eller hörn, på kurvan och lutningen inte går att bestämma). Punkten $\,x=e\,$ är en ändpunkt. När man letar efter extrempunkter hos en funktion gäller det alltså att ta reda på och undersöka alla tänkbara kandidater av punkter. En lämplig arbetsgång är:
Exempel 4 Bestäm alla extrempunkter på kurvan $\,y=3x^4 +4x^3 - 12x^2 + 12\,$.
Derivatan är produkten av dessa faktorer och vi får derivatans tecken genom att multiplicera ihop faktorernas tecken i respektive intervall.
Kurvan har alltså lokala minpunkter i $\,(–2, –20)\,$ och $\,(1, 7)\,$ samt lokal maxpunkt i $\,(0, 12)\,$. Exempel 5 Bestäm alla extrempunkter på kurvan $\,y= x - x^{2/3}\,$.
De kritiska punkterna till funktionen ges av $$\displaystyle y'=0 \quad \Leftrightarrow \quad 1= \frac {2}{3} \cdot \frac{1}{\sqrt[3]{x}}\quad\Leftrightarrow\quad \sqrt[3]{x} = {\textstyle\frac {2}{3}} \quad \Leftrightarrow \quad x = \bigl({\textstyle\frac{2}{3}}\bigr)^3 = {\textstyle\frac{8}{27}}\,\mbox{.}$$ De enda punkter där funktionen eventuellt kan ha extrempunkter är alltså $\,x=0\,$ och $\,x=\frac{8}{27}\,$. För att avgöra dessa punkters karaktär skriver vi upp en teckentabell:
Kurvan har alltså en lokal maximipunkt i $\,(0, 0)\,$ (en spets) och en lokal minimipunkt i $\,(\frac{8}{27},-\frac{4}{27})\,$. [redigera] Absolut max/minEn funktion har ett absolut (eller globalt) maximum (minimum) i en punkt om funktionsvärdet inte är större (mindre) i någon annan punkt i hela definitionsmängden. Ofta kallar man också detta för funktionens största (minsta) värde.
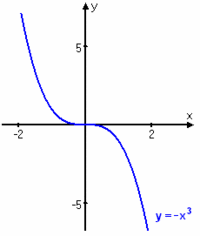
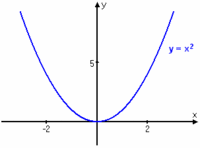
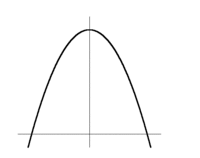
Exempel 6 I den första figuren saknar funktionen såväl globalt maximum som globalt minimum. I den andra figuren saknar funktionen globalt minimum. I tillämpningar ger omständigheterna ofta en begränsad definitionsmängd, dvs. man betraktar endast en del av funktionens graf. Man måste därför vara vaksam på att ett globalt max. eller min. mycket väl kan ligga i intervallets ändpunkter.
Funktionen ovan betraktas endast i intervallet $a\le x \le e$. Vi ser att funktionens minsta värde i detta intervall inträffar i den kritiska punkten $x=b$ , medan största värdet återfinns i ändpunkten $x=e$.
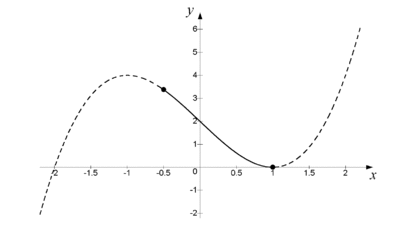
Exempel 7 Bestäm största och minsta värde för funktionen $\,f(x) = x^3 -3x + 2\,$ i intervallet $\,-0{,}5 \le x \le 1\,$.
Figuren visar funktionens hela graf streckad, med den del som ligger inom det givna intervallet heldragen. [redigera] AndraderivatanTecknet på derivatan av en funktion ger oss information om huruvida funktionen är växande eller avtagande. På samma sätt kan andraderivatans tecken visa om förstaderivatan är växande eller avtagande. Detta kan man bl.a. utnyttja för att ta reda på om en given extrempunkt är en max-, eller minpunkt.
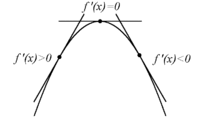
Om funktionen $\,f(x)\,$ har en kritisk punkt i $\,x=a\,$ där $f^{\,\prime\prime}(a)<0$, då gäller att
Om funktionen $\,f(x)\,$ har en kritisk punkt i $\,x=a\,$ där $f^{\,\prime\prime}(a)>0$, då gäller att
Exempel 8 Bestäm alla extrempunkter för funktionen $\,f(x)=x^3 -x^2 -x +2\,$ och bestäm deras karaktär med hjälp av andraderivatan.
|
|