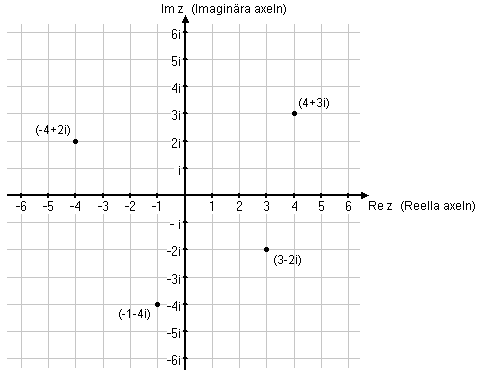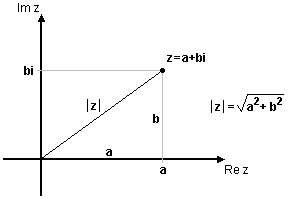3.2 Polär form
Sommarmatte 2
| Versionen från 2 juli 2007 kl. 18.19 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) ← Gå till föregående ändring |
Nuvarande version (3 juli 2007 kl. 07.35) (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst) |
||
| Rad 39: | Rad 39: | ||
| Denna geometriska tolkning av de komplexa talen kallas det <i>komplexa talplanet</i>.<br\> | Denna geometriska tolkning av de komplexa talen kallas det <i>komplexa talplanet</i>.<br\> | ||
| Anm: | Anm: | ||
| - | De reella talen, dvs. alla komplexa tal med imaginärdel $\,0\,$, ligger alltså längs den reella axeln. Man kan alltså se utvidgningen av talsystemet från $\displaystyle\mathbb{R}$ (de reella talen) till $\mathbb{C}$ (de komplexa talen) som att tillföra en ny dimension till den redan fyllda tallinjen. | + | De reella talen, dvs. alla komplexa tal med imaginärdel $\,0\,$, ligger alltså längs den reella axeln. Man kan därför se utvidgningen av talsystemet från $\displaystyle\mathbb{R}$ (de reella talen) till $\mathbb{C}$ (de komplexa talen) som att tillföra en ny dimension till den redan fyllda tallinjen. |
| <br\><br\> | <br\><br\> | ||
| Addition av komplexa tal får helt naturligt en enkel tolkning i det komplexa talplanet och sker geometriskt på samma sätt som vid addition av vektorer: | Addition av komplexa tal får helt naturligt en enkel tolkning i det komplexa talplanet och sker geometriskt på samma sätt som vid addition av vektorer: | ||
| Rad 82: | Rad 82: | ||
| - | För ett komplext tal $\,z=a+bi\,$ definieras absolutbeloppet $\,|z|\,$ som <br\><br\> | + | För ett komplext tal $\,z=a+ib\,$ definieras absolutbeloppet $\,|\,z\,|\,$ som <br\><br\> |
| - | <div class="regel">$$|z|=\sqrt{a^2+b^2}\,\mbox{.}$$</div> | + | <div class="regel">$$|\,z\,|=\sqrt{a^2+b^2}\,\mbox{.}$$</div> |
| - | Vi ser att $\,|z|\,$ är ett reellt tal och att $\,|z|\ge 0\,$. För reella tal är $\,b = 0\,$ och då gäller att $\,|z|=\sqrt{a^2}=|a|\,$, vilket överensstämmer med den vanliga definitionen för absolutbelopp av reella tal. | + | Vi ser att $\,|\,z\,|\,$ är ett reellt tal och att $\,|\,z\,|\ge 0\,$. För reella tal är $\,b = 0\,$ och då gäller att $\,|\,z\,|=\sqrt{a^2}=|\,a\,|\,$, vilket överensstämmer med den vanliga definitionen för absolutbelopp av reella tal. |
| - | Geometriskt är absolutbeloppet avståndet från talet $\,z=a+bi\,$ (punkten $\,(a, b)\,$) till $\,z = 0\,$ (origo), enligt Pythagoras sats.<br\> | + | Geometriskt är absolutbeloppet avståndet från talet $\,z=a+ib\,$ (punkten $\,(a, b)\,$) till $\,z = 0\,$ (origo), enligt Pythagoras sats.<br\> |
| <div align="center">[[Bild:komplext-talplan-5.gif||center|]]</div> | <div align="center">[[Bild:komplext-talplan-5.gif||center|]]</div> | ||
| ==Avstånd mellan komplexa tal== | ==Avstånd mellan komplexa tal== | ||
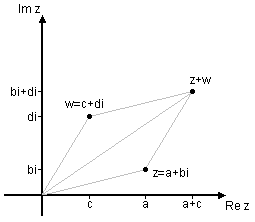
| - | Med hjälp av formeln för avstånd mellan punkter i ett koordinatsystem får man också en viktig och användbar tolkning av absolutbelopp. Avståndet $\,s\,$ mellan två komplexa tal $\,z=a+bi\,$ och $\,w=c+di\,$ (se fig.) kan med hjälp av avståndsformeln skrivas <br\> | + | Med hjälp av formeln för avstånd mellan punkter i ett koordinatsystem får man också en viktig och användbar tolkning av absolutbelopp. Avståndet $\,s\,$ mellan två komplexa tal $\,z=a+ib\,$ och $\,w=c+id\,$ (se fig.) kan med hjälp av avståndsformeln skrivas <br\> |
| <div class="regel">$$s=\sqrt{(a-c)^2+(b-d)^2}\,\mbox{.}$$</div> | <div class="regel">$$s=\sqrt{(a-c)^2+(b-d)^2}\,\mbox{.}$$</div> | ||
| [[Bild:komplext-talplan-6.gif||center|]]<br> | [[Bild:komplext-talplan-6.gif||center|]]<br> | ||
| - | Eftersom $\,z-w=(a-c)+(b-d)i\,$, så får man att <br> | + | Eftersom $\,z-w=(a-c)+i(b-d)\,$, så får man att <br> |
| - | <center>$|z-w|=\sqrt{(a-c)^2+(b-d)^2}={}$avståndet mellan talen $\,z\,$ och $\,w\,$.</center> | + | <center>$|\,z-w\,|=\sqrt{(a-c)^2+(b-d)^2}={}$avståndet mellan talen $\,z\,$ och $\,w\,$.</center> |
| Rad 102: | Rad 102: | ||
| <br/> | <br/> | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li>$\,\, |z|=2$ | + | <li>$\,\, |\,z\,|=2$ |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
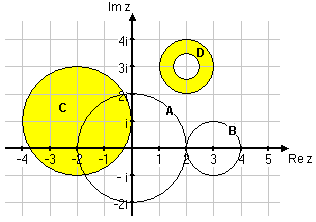
| Ekvationen beskriver alla tal vars avstånd till origo är 2. Dessa tal bildar i det komplexa talplanet en cirkel med radien 2 och medelpunkt i origo.</li> | Ekvationen beskriver alla tal vars avstånd till origo är 2. Dessa tal bildar i det komplexa talplanet en cirkel med radien 2 och medelpunkt i origo.</li> | ||
| <br/> | <br/> | ||
| - | <li>$\,\, |z-3|=1$ | + | <li>$\,\, |\,z-3\,|=1$ |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| Rad 113: | Rad 113: | ||
| </li> | </li> | ||
| <br/> | <br/> | ||
| - | <li>$\,\, |z+2-i|\le 2$ | + | <li>$\,\, |\,z+2-i\,|\le 2$ |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| - | Vänsterledet kan skrivas $\,|z-(-2+i)|\,$, vilket innebär alla tal på avståndet ${}\le 2$ från talet $\,-2+i\,$, dvs. en cirkelskiva med radien 2 och medelpunkt i $\,-2+i\,$. | + | Vänsterledet kan skrivas $\,|\,z-(-2+i)\,|\,$, vilket innebär alla tal på avståndet ${}\le 2$ från talet $\,-2+i\,$, dvs. en cirkelskiva med radien 2 och medelpunkt i $\,-2+i\,$. |
| </li> | </li> | ||
| <br/> | <br/> | ||
| - | <li>$\,\, \frac{1}{2}\le |z-(2+3i)|\le 1$ | + | <li>$\,\, \frac{1}{2}\le |\,z-(2+3i)\,|\le 1$ |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| Rad 132: | Rad 132: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 4'''<br\> | + | '''Exempel 4'''<br/><br/> |
| Markera i det komplexa talplanet alla tal $\,z\,$ som uppfyller villkoren | Markera i det komplexa talplanet alla tal $\,z\,$ som uppfyller villkoren | ||
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| <ol type="a"> | <ol type="a"> | ||
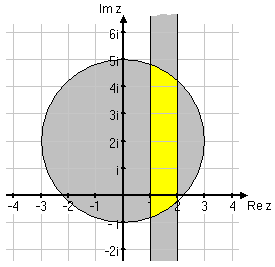
| - | <li>$\, \left\{ \eqalign{&|z-2i|\le 3\cr &1\le\mathop{\rm Re} z\le 2}\right.$ | + | <li>$\, \left\{ \eqalign{&|\,z-2i\,|\le 3\cr &1\le\mathop{\rm Re} z\le 2}\right.$ |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
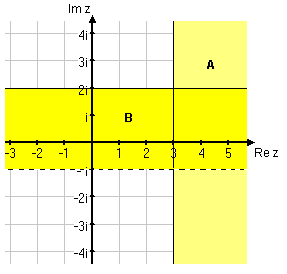
| - | Den första olikheten ger punkterna på och innanför cirkeln med radie 3 och medelpunkt i $\,2i\,$. Den andra olikheten ger ett vertikalt band av punkter med realdel mellan 1 och 2. Det område som uppfyller båda olikheter ges av de punkter som ligger inom cirkeln och bandet. | + | Den första olikheten ger punkterna på och innanför cirkeln med radie 3 och medelpunkt i $\,2i\,$. Den andra olikheten ger ett vertikalt band av punkter med realdel mellan 1 och 2. Det område som uppfyller de båda olikheterna ges av de punkter som samtidigt ligger inom cirkeln och bandet. |
| </li> | </li> | ||
| <br/> | <br/> | ||
| - | <li>$\, |z+1|=|z-2|$ | + | <li>$\, |\,z+1\,|=|\,z-2\,|$ |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| - | Ekvationen kan skrivas $\,|z-(-1)|=|z-2|\,$. Man ser då att $\,z\,$ ska ligga på samma avstånd från $\,-1\,$ som från $\,2\,$. Detta villkor uppfylls av alla tal $\,z\,$ som har realdel $\,1/2\,$. | + | Ekvationen kan skrivas $\,|\,z-(-1)\,|=|\,z-2\,|\,$. Man ser då att $\,z\,$ ska ligga på samma avstånd från $\,-1\,$ som från $\,2\,$. Detta villkor uppfylls av alla tal $\,z\,$ som har realdel $\,1/2\,$. |
| </li> | </li> | ||
| </ol> | </ol> | ||
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| - | <center>[[Bild:komplext-talplan-8.gif|Området i deluppgift a]][[Bild:komplext-talplan-10.gif|Området i deluppgift b]]</center> | + | <center>[[Bild:komplext-talplan-8.gif|||Området i deluppgift a]][[Bild:komplext-talplan-10.gif|||Området i deluppgift b]]</center> |
| Rad 157: | Rad 157: | ||
| ==Polär form== | ==Polär form== | ||
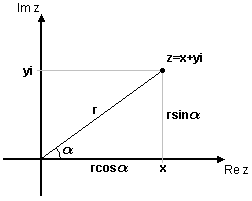
| - | I stället för att ange ett komplext tal $\,z=x+iy\,$ i dess rektangulära koordinater $\,(x,y)\,$ kan man använda polära koordinater. Detta innebär att man anger talets läge i det komplexa talplanet genom dess avstånd, $\,r\,$, till origo, samt den vinkel $\,\alpha\,$ som som bildas mellan den positiva ''x''-axeln och sträckan från origo till talet (se figuren). | + | I stället för att ange ett komplext tal $\,z=x+iy\,$ i dess rektangulära koordinater $\,(x,y)\,$ kan man använda polära koordinater. Detta innebär att man anger talets läge i det komplexa talplanet genom dess avstånd, $\,r\,$, till origo, samt den vinkel $\,\alpha\,$ som bildas mellan den positiva ''x''-axeln och sträckan från origo till talet (se figuren). |
| [[Bild:komplext-talplan-11.gif||center|]] | [[Bild:komplext-talplan-11.gif||center|]] | ||
| Eftersom $\ \cos\alpha = x/r\ $ och $\ \sin\alpha = y/r\ $ så är $\ x = r\cos\alpha\ $ och $\ y= r\sin\alpha\,$. Talet $\,z=x+iy\,$ kan därför skrivas som | Eftersom $\ \cos\alpha = x/r\ $ och $\ \sin\alpha = y/r\ $ så är $\ x = r\cos\alpha\ $ och $\ y= r\sin\alpha\,$. Talet $\,z=x+iy\,$ kan därför skrivas som | ||
| - | <div class="regel">$$z=r\cos\alpha + ir\sin\alpha = r(\cos\alpha + i\sin\alpha)\,\mbox{,}$$</div> | + | <div class="regel">$$z=r\cos\alpha + i\,r\sin\alpha = r(\cos\alpha + i\,\sin\alpha)\,\mbox{,}$$</div> |
| vilket kallas den <i>polära formen</i> av ett komplext tal $\,z\,$. Vinkeln $\,\alpha\,$ kallas <i>argumentet</i> för $\,z\,$ och skrivs | vilket kallas den <i>polära formen</i> av ett komplext tal $\,z\,$. Vinkeln $\,\alpha\,$ kallas <i>argumentet</i> för $\,z\,$ och skrivs | ||
| <div class="regel">$$\alpha=\arg z\,\mbox{.}$$</div> | <div class="regel">$$\alpha=\arg z\,\mbox{.}$$</div> | ||
| Vinkeln $\,\alpha\,$ kan t.ex. bestämmas genom att lösa ekvationen $\,\tan\alpha=y/x\,$. Denna ekvation har dock flera lösningar, varför man måste se till att man väljer den lösning $\,\alpha\,$ som gör att $\,z= r(\cos\alpha + i\sin\alpha)\,$ hamnar i rätt kvadrant. | Vinkeln $\,\alpha\,$ kan t.ex. bestämmas genom att lösa ekvationen $\,\tan\alpha=y/x\,$. Denna ekvation har dock flera lösningar, varför man måste se till att man väljer den lösning $\,\alpha\,$ som gör att $\,z= r(\cos\alpha + i\sin\alpha)\,$ hamnar i rätt kvadrant. | ||
| + | Argumentet till ett komplext tal är inte heller unikt bestämt eftersom vinklar som skiljer sig åt med $\,2\pi\,$ anger samma riktning i det komplexa talplanet. Normalt brukar man dock ange argumentet som en vinkel mellan 0 och $\,2\pi\,$ eller mellan $\,-\pi\,$ och $\,\pi\,$. | ||
| - | Det reella talet $\,r\,$, avståndet till origo, känner vi redan som beloppet av $\,z\,$, eftersom | + | |
| + | Det reella talet $\,r\,$, avståndet till origo, känner vi redan som beloppet av $\,z\,$, | ||
| <div class="regel">$$r=\sqrt{x^2+y^2}=|\,z\,|$$</div> | <div class="regel">$$r=\sqrt{x^2+y^2}=|\,z\,|$$</div> | ||
| Rad 172: | Rad 174: | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
| <br/> | <br/> | ||
| - | Skriv följande komplexa tal på polär form: | + | <br/> |
| + | Skriv följande komplexa tal i polär form: | ||
| <ol type="a"> | <ol type="a"> | ||
| <li>$\,\,-3$ | <li>$\,\,-3$ | ||
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| - | Vi har att $\,|\,-3\,|=3\,$ och $\,\arg (-3)=\pi\,$, vilket betyder att $\,-3=3(\cos\pi+i\,\sin\pi)\,$. | + | Vi har att $\,|\,-3\,|=3\,$ och $\,\arg (-3)=\pi\,$, vilket betyder att $\ -3=3(\cos\pi+i\,\sin\pi)\,$. |
| </li> | </li> | ||
| <br/> | <br/> | ||
| Rad 183: | Rad 186: | ||
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| - | Vi har att $\,|\,i\,|=1\,$ och $\,\arg i = \pi/2\,$ så i polär form är $\,i=\cos(\pi/2)+i\,\sin(\pi/2)\,$. | + | Vi har att $\,|\,i\,|=1\,$ och $\,\arg i = \pi/2\,$ så i polär form är $\ i=\cos(\pi/2)+i\,\sin(\pi/2)\,$. |
| </li> | </li> | ||
| <br/> | <br/> | ||
| Rad 189: | Rad 192: | ||
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| - | Formeln för beloppet av ett komplext tal ger att $\,|\,1-i\,|=\sqrt{1^2+(-1)^2}=\sqrt{2}\,$. Det komplexa talet ligger i den fjärde kvadranten och bildar vinkeln $\,\pi/4\,$ med den positiva reella axeln, vilket ger att $\,\arg (1-i)=2\pi-\pi/4=7\pi/4$. Alltså är $\,1-i=\sqrt{2}\,(\cos(7\pi/4)+i\sin(7\pi/4)\,)$. | + | Formeln för beloppet av ett komplext tal ger att $\,|\,1-i\,|=\sqrt{1^2+(-1)^2}=\sqrt{2}\,$. Det komplexa talet ligger i den fjärde kvadranten och bildar vinkeln $\,\pi/4\,$ med den positiva reella axeln, vilket ger att $\,\arg (1-i)=2\pi-\pi/4=7\pi/4$. Alltså är $\ 1-i=\sqrt{2}\,\bigl(\cos(7\pi/4)+i\sin(7\pi/4)\,\bigr)\,$. |
| </li> | </li> | ||
| <br/> | <br/> | ||
| Rad 196: | Rad 199: | ||
| <br/> | <br/> | ||
| Beloppet är enklast att räkna ut | Beloppet är enklast att räkna ut | ||
| - | $$|\,2\sqrt{3}+2i\,|=\sqrt{(2\sqrt{3})^2+2^2}=\sqrt{16}=4\,\mbox{.}$$ | + | $$|\,2\sqrt{3}+2i\,|=\sqrt{(2\sqrt{3}\,)^2+2^2}=\sqrt{16}=4\,\mbox{.}$$ |
| - | Om vi kallar argumentet för $\alpha$ så uppfyller det sambandet | + | Om vi kallar argumentet för $\,\alpha\,$ så uppfyller det sambandet |
| $$\tan\alpha=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}$$ | $$\tan\alpha=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}$$ | ||
| och eftersom talet ligger i den första kvadranten (positiv real- och imaginärdel) så är $\,\alpha=\pi/6\,$ och vi har att | och eftersom talet ligger i den första kvadranten (positiv real- och imaginärdel) så är $\,\alpha=\pi/6\,$ och vi har att | ||
| Rad 209: | Rad 212: | ||
| ==Multiplikation och division i polär form== | ==Multiplikation och division i polär form== | ||
| - | Den stora fördelen med att ha komplexa tal skrivna i polär form är att multiplikation och division då blir väldigt enkla att utföra. För godtyckliga komplexa tal $\,z=|z|(\cos\alpha+i\sin\alpha)\,$ och $\,w=|w|(\cos\beta+i\sin\beta)\,$ kan man genom de trigonometriska additionsformlerna visa att | + | Den stora fördelen med att ha komplexa tal skrivna i polär form är att multiplikation och division då blir väldigt enkla att utföra. För godtyckliga komplexa tal $\,z=|\,z\,|\,(\cos\alpha+i\sin\alpha)\,$ och $\,w=|\,w\,|\,(\cos\beta+i\sin\beta)\,$ kan man genom de trigonometriska additionsformlerna visa att |
| <div class="regel"> | <div class="regel"> | ||
| - | $$\eqalign{z\cdot w&=|z|\cdot |w|\left(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\right)\,\mbox{,}\cr \frac{z}{w}&=\frac{|z|}{|w|}\left(\cos(\alpha-\beta)+i\sin(\alpha-\beta)\right)\,\mbox{.}}$$ | + | $$\eqalign{z\cdot w&=|\,z\,|\,|\,w\,|\,\bigl(\cos(\alpha+\beta)+i\,\sin(\alpha+\beta)\bigr)\,\mbox{,}\cr \frac{z}{w}&=\frac{|z|}{|w|}\bigl(\cos(\alpha-\beta)+i\,\sin(\alpha-\beta)\bigr)\,\mbox{.}}$$ |
| </div> | </div> | ||
| Vid multiplikation av komplexa tal <i>multipliceras</i> alltså beloppen, medan argumenten <i>adderas</i>. | Vid multiplikation av komplexa tal <i>multipliceras</i> alltså beloppen, medan argumenten <i>adderas</i>. | ||
| Vid division av komplexa tal <i>divideras</i> beloppen och argumenten <i>subtraheras</i>. Detta kan kortfattat skrivas: | Vid division av komplexa tal <i>divideras</i> beloppen och argumenten <i>subtraheras</i>. Detta kan kortfattat skrivas: | ||
| <div class="regel"> | <div class="regel"> | ||
| - | $$|z\cdot w|=|z|\cdot |w|\quad \mbox{och}\quad \arg(z\cdot w)=\arg\,z + \arg\,w\,\mbox{,}$$ | + | $$|\,z\cdot w\,|=|\,z\,|\cdot |\,w\,|\quad \mbox{och}\quad \arg(z\cdot w)=\arg\,z + \arg\,w\,\mbox{,}$$ |
| - | $$\left|\frac{z}{w}\right|=\frac{|z|}{|w|}\quad\quad\quad\; \mbox{ och}\quad \arg\left(\frac{z}{w}\right)=\arg\,z - \arg\,w\,\mbox{.}$$ | + | $$\Bigl|\,\frac{z}{w}\,\Bigr|=\frac{|\,z\,|}{|\,w\,|}\quad\quad\quad\; \mbox{ och}\quad \arg\Bigl(\frac{z}{w}\Bigr)=\arg \,z - \arg\,w\,\mbox{.}$$ |
| </div> | </div> | ||
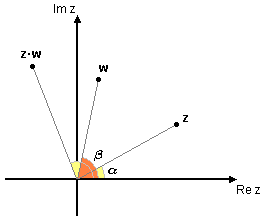
| - | I det komplexa talplanet innebär alltså en multiplikation av $\,z\,$ med $\,w\,$ att $\,z\,$ förlängs med faktorn $\,|w|\,$ och roteras moturs med vinkeln $\,\arg\,w\,$. | + | I det komplexa talplanet innebär alltså en multiplikation av $\,z\,$ med $\,w\,$ att $\,z\,$ förlängs med faktorn $\,|\,w\,|\,$ och roteras moturs med vinkeln $\,\arg\,w\,$. |
| [[Bild:komplext-talplan-13.gif||center|]] | [[Bild:komplext-talplan-13.gif||center|]] | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 6''' | '''Exempel 6''' | ||
| - | <br\> | + | <br/> |
| + | <br/> | ||
| Beräkna följande uttryck och genom att skriva om på polär form: | Beräkna följande uttryck och genom att skriva om på polär form: | ||
| <ol type="a"> | <ol type="a"> | ||
| Rad 233: | Rad 237: | ||
| $$\eqalign{\Bigl(\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) &= 1\cdot\Bigl(\cos\frac{7\pi}{4}+i\,\sin\frac{7\pi}{4}\Bigr)\cr \Bigr(-\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr) &= 1\cdot\Bigl(\cos\frac{3\pi}{4}+i\,\sin\frac{3\pi}{4}\Bigr)}$$ | $$\eqalign{\Bigl(\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) &= 1\cdot\Bigl(\cos\frac{7\pi}{4}+i\,\sin\frac{7\pi}{4}\Bigr)\cr \Bigr(-\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr) &= 1\cdot\Bigl(\cos\frac{3\pi}{4}+i\,\sin\frac{3\pi}{4}\Bigr)}$$ | ||
| och då följer att | och då följer att | ||
| - | $$\eqalign{&\Bigl(\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) \Big/ \Bigl(-\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr) = \smash{\frac{\displaystyle\cos\frac{7}{4\pi}+i\,\sin\frac{7\pi}{4}\vphantom{\Biggl(}}{\displaystyle\cos\frac{3\pi}{4}+i\,\sin\frac{3\pi}{4}\vphantom{\Biggl)}}}\cr &\qquad\quad{}= \cos\Bigl(\frac{7\pi}{4}-\frac{3\pi}{4}\Bigl)+i\,\sin\Bigl(\frac{7\pi}{4}-\frac{3\pi}{4}\Bigr)= \cos\pi+i\,\sin\pi=-1\,\mbox{.}\vphantom{\Biggr)^{\Bigl(}}}$$ | + | $$\eqalign{&\Bigl(\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) \Big/ \Bigl(-\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr) = \smash{\frac{\displaystyle\cos\frac{7\pi}{4}+i\,\sin\frac{7\pi}{4}\vphantom{\Biggl(}}{\displaystyle\cos\frac{3\pi}{4}+i\,\sin\frac{3\pi}{4}\vphantom{\Biggl)}}}\cr &\qquad\quad{}= \cos\Bigl(\frac{7\pi}{4}-\frac{3\pi}{4}\Bigl)+i\,\sin\Bigl(\frac{7\pi}{4}-\frac{3\pi}{4}\Bigr)= \cos\pi+i\,\sin\pi=-1\,\mbox{.}\vphantom{\Biggr)^{\Bigl(}}}$$ |
| </li> | </li> | ||
| <br/> | <br/> | ||
| Rad 242: | Rad 246: | ||
| $$\eqalign{(-2-2i)&=\sqrt8\Bigl(\cos\frac{5\pi}{4}+i\,\sin\frac{5\pi}{4}\Bigr)\,\mbox{,}\cr (1+i)&=\sqrt2\Bigl(\cos\frac{\pi}{4}+i\,\sin\frac{\pi}{4}\Bigr)\,\mbox{.}}$$ | $$\eqalign{(-2-2i)&=\sqrt8\Bigl(\cos\frac{5\pi}{4}+i\,\sin\frac{5\pi}{4}\Bigr)\,\mbox{,}\cr (1+i)&=\sqrt2\Bigl(\cos\frac{\pi}{4}+i\,\sin\frac{\pi}{4}\Bigr)\,\mbox{.}}$$ | ||
| Genom att utföra multiplikationen i polär form får vi att | Genom att utföra multiplikationen i polär form får vi att | ||
| - | $$\eqalign{(-2-2i)(1+i)&=\sqrt8 \cdot \sqrt2\,\Bigl(\cos\Bigl(\frac{5\pi}{4}+\frac{\pi}{4}\Bigr)+i\,\sin\Bigl(\frac{5\pi}{4}+\frac{\pi}{4}\Bigr)\Bigr)\cr &=4\cos\Bigl(\cos\frac{3\pi}{2}+i\,\sin\frac{3\pi}{2} \Bigr)=-4i\,\mbox{.}}$$ | + | $$\eqalign{(-2-2i)(1+i)&=\sqrt8 \cdot \sqrt2\,\Bigl(\cos\Bigl(\frac{5\pi}{4}+\frac{\pi}{4}\Bigr)+i\,\sin\Bigl(\frac{5\pi}{4}+\frac{\pi}{4}\Bigr)\Bigr)\cr &=4\Bigl(\cos\frac{3\pi}{2}+i\,\sin\frac{3\pi}{2} \Bigr)=-4i\,\mbox{.}}$$ |
| </li> | </li> | ||
| <br/> | <br/> | ||
| Rad 250: | Rad 254: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 7''' | '''Exempel 7''' | ||
| - | <br\> | + | <br/> |
| - | + | <br/> | |
| <ol type="a"> | <ol type="a"> | ||
| <li>Beräkna $\,iz\,$ och $\,\displaystyle\frac{z}{i}\,$ om $\ \displaystyle z=2\Bigl(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\Bigr)\,$. Svara på polär form. | <li>Beräkna $\,iz\,$ och $\,\displaystyle\frac{z}{i}\,$ om $\ \displaystyle z=2\Bigl(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\Bigr)\,$. Svara på polär form. | ||
| Rad 257: | Rad 261: | ||
| <br/> | <br/> | ||
| Eftersom $\ \displaystyle i=1\cdot \left(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\right)\ $ så är | Eftersom $\ \displaystyle i=1\cdot \left(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\right)\ $ så är | ||
| - | $$\eqalign{iz&=2\Bigl(\cos\Bigl(\frac{\pi}{6}+\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{\pi}{6}+\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}\Bigr)\cr \frac{i}{z}&=2\Bigl(\cos\Bigl(\frac{\pi}{6}-\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{\pi}{6}-\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{-\pi}{3}+i\,\sin\frac{-\pi}{3}\Bigr)}$$ | + | $$\eqalign{iz&=2\Bigl(\cos\Bigl(\frac{\pi}{6}+\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{\pi}{6}+\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}\Bigr)\,\mbox{,}\cr \frac{z}{i}&=2\Bigl(\cos\Bigl(\frac{\pi}{6}-\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{\pi}{6}-\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{-\pi}{3}+i\,\sin\frac{-\pi}{3}\Bigr)\,\mbox{.}}$$ |
| </li> | </li> | ||
| <br/> | <br/> | ||
| - | <li> Beräkna $iz$ och $\displaystyle\frac{z}{i}$ om $\displaystyle z=3\left(\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}\right)\,$. Svara på polär form. | + | <li> Beräkna $\,iz\,$ och $\,\displaystyle\frac{z}{i}\,$ om $\ \displaystyle z=3\left(\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}\right)\,$. Svara på polär form. |
| <br/> | <br/> | ||
| <br/> | <br/> | ||
| Använder vi den polära formen av $\,i\,$ så fås att | Använder vi den polära formen av $\,i\,$ så fås att | ||
| - | $$\eqalign{iz&=3\Bigl(\cos\Bigl(\frac{7\pi}{4}+\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{7\pi}{4}+\frac{\pi}{2}\Bigr)\,\Bigr) =3\Bigl(\cos\frac{9\pi}{4}+i\sin\frac{9\pi}{4}\Bigr)\cr &=3\left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right)\cr \frac{i}{z}&=2\Bigl(\cos\Bigl(\frac{7\pi}{4}-\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{7\pi}{4}-\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{5\pi}{4}+i\,\sin\frac{5\pi}{4}\Bigr)}$$ | + | $$\eqalign{iz&=3\Bigl(\cos\Bigl(\frac{7\pi}{4}+\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{7\pi}{4}+\frac{\pi}{2}\Bigr)\,\Bigr) =3\Bigl(\cos\frac{9\pi}{4}+i\sin\frac{9\pi}{4}\Bigr)\cr &=3\left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right)\,\mbox{,}\cr \frac{z}{i}&=2\Bigl(\cos\Bigl(\frac{7\pi}{4}-\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{7\pi}{4}-\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{5\pi}{4}+i\,\sin\frac{5\pi}{4}\Bigr)\,\mbox{.}}$$ |
| </li> | </li> | ||
| <br/> | <br/> | ||
| </ol> | </ol> | ||
| Vi ser här att multiplikation med $\,i\,$ innebär en rotation $\,\pi/2\,$ moturs, medan division med $\,i\,$ medför en rotation $\,\pi/2\,$ medurs. | Vi ser här att multiplikation med $\,i\,$ innebär en rotation $\,\pi/2\,$ moturs, medan division med $\,i\,$ medför en rotation $\,\pi/2\,$ medurs. | ||
| - | <center>[[Bild:komplext-talplan-14.gif|Deluppgift a]][[Bild:komplext-talplan-15.gif|Deluppgift b]]</center> | + | <center>[[Bild:komplext-talplan-14.gif|||Deluppgift a]][[Bild:komplext-talplan-15.gif|||Deluppgift b]]</center> |
| </div> | </div> | ||
| - | <div class="inforuta"> | ||
| - | '''Råd för inläsning''' | ||
| - | |||
| - | '''Tänk på att:''' | ||
| - | |||
| - | text | ||
| - | |||
| - | '''Lästips''' | ||
| - | |||
| - | stående | ||
| - | |||
| - | '''Länktips''' | ||
| - | |||
| - | stående | ||
| - | |||
| - | </div> | ||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
[redigera] Det komplexa talplanetEftersom ett komplext tal $\,z=a+bi\,$ består av en realdel $\,a\,$ och en imaginärdel $\,b\,$, så kan $\,z\,$ betraktas som ett ordnat talpar $\,(a,b)\,$ och tolkas som en punkt i ett koordinatsystem. Man bildar därför ett koordinatsystem genom att ställa en imaginär axel (en tallinje med enheten $\,i\,$) vinkelrät mot en reell axel (den reella tallinjen). Vi kan nu beskriva varje komplext tal med en punkt i detta koordinatsystem, och varje punkt beskriver ett unikt komplext tal.
Denna geometriska tolkning av de komplexa talen kallas det komplexa talplanet.
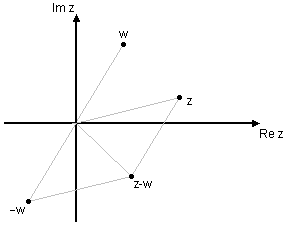
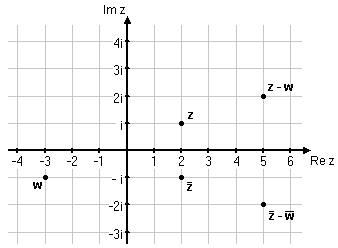
Exempel 1 Givet $\,z=2+i\,$ och $\,w=-3-i\,$. Markera $\,z\,$, $\,w\,$, $\,\overline{z}\,$, $\,\overline{z}-\overline{w}\,$ och $\,z-w\,$ i det komplexa talplanet.
Exempel 2
[redigera] AbsolutbeloppDe reella talen går att ordna i storleksordning, dvs. vi kan avgöra om ett reellt tal är större än ett annat; ju längre till höger på den reella tallinjen desto större är talet. För de komplexa talen saknar man denna möjlighet. Vi kan inte utan vidare avgöra vilket tal som är störst av t.ex. $\,z=1-i\,$ och $\,w=-1+i\,$ . Med hjälp av begreppet absolutbelopp kan vi dock definiera ett mått på storleken av ett komplext tal.
$$|\,z\,|=\sqrt{a^2+b^2}\,\mbox{.}$$
Vi ser att $\,|\,z\,|\,$ är ett reellt tal och att $\,|\,z\,|\ge 0\,$. För reella tal är $\,b = 0\,$ och då gäller att $\,|\,z\,|=\sqrt{a^2}=|\,a\,|\,$, vilket överensstämmer med den vanliga definitionen för absolutbelopp av reella tal.
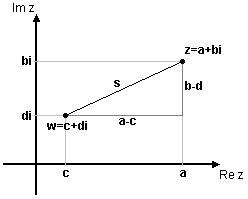
Geometriskt är absolutbeloppet avståndet från talet $\,z=a+ib\,$ (punkten $\,(a, b)\,$) till $\,z = 0\,$ (origo), enligt Pythagoras sats. [redigera] Avstånd mellan komplexa talMed hjälp av formeln för avstånd mellan punkter i ett koordinatsystem får man också en viktig och användbar tolkning av absolutbelopp. Avståndet $\,s\,$ mellan två komplexa tal $\,z=a+ib\,$ och $\,w=c+id\,$ (se fig.) kan med hjälp av avståndsformeln skrivas $$s=\sqrt{(a-c)^2+(b-d)^2}\,\mbox{.}$$
Eftersom $\,z-w=(a-c)+i(b-d)\,$, så får man att
Exempel 3
Exempel 4
 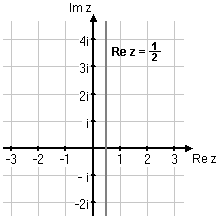
[redigera] Polär formI stället för att ange ett komplext tal $\,z=x+iy\,$ i dess rektangulära koordinater $\,(x,y)\,$ kan man använda polära koordinater. Detta innebär att man anger talets läge i det komplexa talplanet genom dess avstånd, $\,r\,$, till origo, samt den vinkel $\,\alpha\,$ som bildas mellan den positiva x-axeln och sträckan från origo till talet (se figuren). Eftersom $\ \cos\alpha = x/r\ $ och $\ \sin\alpha = y/r\ $ så är $\ x = r\cos\alpha\ $ och $\ y= r\sin\alpha\,$. Talet $\,z=x+iy\,$ kan därför skrivas som $$z=r\cos\alpha + i\,r\sin\alpha = r(\cos\alpha + i\,\sin\alpha)\,\mbox{,}$$
vilket kallas den polära formen av ett komplext tal $\,z\,$. Vinkeln $\,\alpha\,$ kallas argumentet för $\,z\,$ och skrivs $$\alpha=\arg z\,\mbox{.}$$
Vinkeln $\,\alpha\,$ kan t.ex. bestämmas genom att lösa ekvationen $\,\tan\alpha=y/x\,$. Denna ekvation har dock flera lösningar, varför man måste se till att man väljer den lösning $\,\alpha\,$ som gör att $\,z= r(\cos\alpha + i\sin\alpha)\,$ hamnar i rätt kvadrant. Argumentet till ett komplext tal är inte heller unikt bestämt eftersom vinklar som skiljer sig åt med $\,2\pi\,$ anger samma riktning i det komplexa talplanet. Normalt brukar man dock ange argumentet som en vinkel mellan 0 och $\,2\pi\,$ eller mellan $\,-\pi\,$ och $\,\pi\,$.
$$r=\sqrt{x^2+y^2}=|\,z\,|$$
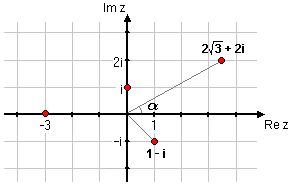
Exempel 5
[redigera] Multiplikation och division i polär formDen stora fördelen med att ha komplexa tal skrivna i polär form är att multiplikation och division då blir väldigt enkla att utföra. För godtyckliga komplexa tal $\,z=|\,z\,|\,(\cos\alpha+i\sin\alpha)\,$ och $\,w=|\,w\,|\,(\cos\beta+i\sin\beta)\,$ kan man genom de trigonometriska additionsformlerna visa att $$\eqalign{z\cdot w&=|\,z\,|\,|\,w\,|\,\bigl(\cos(\alpha+\beta)+i\,\sin(\alpha+\beta)\bigr)\,\mbox{,}\cr \frac{z}{w}&=\frac{|z|}{|w|}\bigl(\cos(\alpha-\beta)+i\,\sin(\alpha-\beta)\bigr)\,\mbox{.}}$$ Vid multiplikation av komplexa tal multipliceras alltså beloppen, medan argumenten adderas. Vid division av komplexa tal divideras beloppen och argumenten subtraheras. Detta kan kortfattat skrivas: $$|\,z\cdot w\,|=|\,z\,|\cdot |\,w\,|\quad \mbox{och}\quad \arg(z\cdot w)=\arg\,z + \arg\,w\,\mbox{,}$$ $$\Bigl|\,\frac{z}{w}\,\Bigr|=\frac{|\,z\,|}{|\,w\,|}\quad\quad\quad\; \mbox{ och}\quad \arg\Bigl(\frac{z}{w}\Bigr)=\arg \,z - \arg\,w\,\mbox{.}$$ I det komplexa talplanet innebär alltså en multiplikation av $\,z\,$ med $\,w\,$ att $\,z\,$ förlängs med faktorn $\,|\,w\,|\,$ och roteras moturs med vinkeln $\,\arg\,w\,$. Exempel 6
Exempel 7
Vi ser här att multiplikation med $\,i\,$ innebär en rotation $\,\pi/2\,$ moturs, medan division med $\,i\,$ medför en rotation $\,\pi/2\,$ medurs. 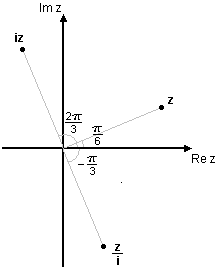 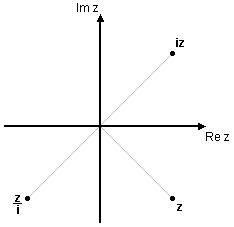
© Copyright 2007, math.se
|