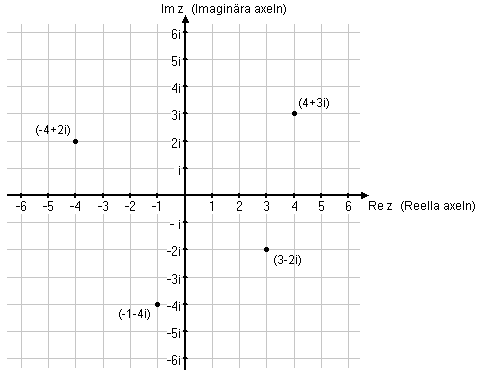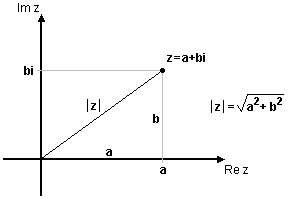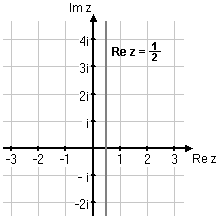3.2 Polär form
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 2 juli 2007 kl. 13.05 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) ← Gå till föregående ändring |
Versionen från 2 juli 2007 kl. 14.40 (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) Gå till nästa ändring → |
||
| Rad 57: | Rad 57: | ||
| <br/> | <br/> | ||
| Vi har att | Vi har att | ||
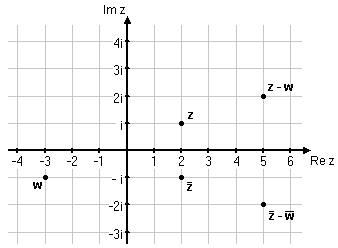
| - | $$\eqalign{\overline{z}&=2-i\cr \overline{w}&=-3+i\cr z-w&=2+i-(-3-i)=5+2i\cr \overline{z} -\overline{w} &= 2-i -(-3+i)=5-2i\quad ({}=\overline{z-w}\,)}$$ | + | *$\overline{z}=2-i$ |
| + | *$\overline{w}=-3+i$ | ||
| + | *$z-w=2+i-(-3-i)=5+2i$ | ||
| + | *$\overline{z} -\overline{w} = 2-i -(-3+i)=5-2i\quad ({}=\overline{z-w})$ | ||
| [[Bild:komplext-talplan-4.gif||center|]] | [[Bild:komplext-talplan-4.gif||center|]] | ||
| </div> | </div> | ||
| Rad 63: | Rad 66: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 2'''<br\> | '''Exempel 2'''<br\> | ||
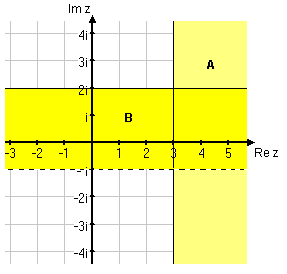
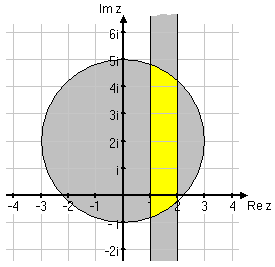
| - | Markera i det komplexa talplanet alla tal $z$ som uppfyller följande villkor: <br\> | + | Markera i det komplexa talplanet alla tal $\,z\,$ som uppfyller följande villkor: <br\> |
| - | <b>A:</b> $\mbox{Re} \, z \ge 3$<br\> | + | <ol type="a"> |
| - | <b>B:</b> -1 < $\mbox{Im} \, z \le 2$<br\><br\> | + | <li>$\mathop{\rm Re} z \ge 3$</li> |
| - | <i>Lösning</i>:<br\> | + | <li>$ -1 < \mathop{\rm Im} z \le 2$</li> |
| - | [[Bild:komplext-talplan-9.gif]] | + | </ol> |
| + | <br/> | ||
| + | Den första olikheten definierar området markerat med A i figuren nedan och den andra olikheten området B. | ||
| + | [[Bild:komplext-talplan-9.gif||center|]] | ||
| </div> | </div> | ||
| ==Absolutbelopp== | ==Absolutbelopp== | ||
| - | De reella talen går att ordna i storleksordning, dvs. vi kan avgöra om ett reellt tal är större än ett annat; ju längre till höger på den reella tallinjen desto större är talet. <br\> | + | De reella talen går att ordna i storleksordning, dvs. vi kan avgöra om ett reellt tal är större än ett annat; ju längre till höger på den reella tallinjen desto större är talet. |
| - | För de komplexa talen saknar man denna möjlighet. Vi kan inte utan vidare avgöra vilket tal som är störst av t.ex. $z=1-i$ och $w=-1+i$ . Med hjälp av begreppet <i>absolutbelopp</i> kan vi dock definiera ett mått på storleken av ett komplext tal.<br\><br\> | + | |
| - | För ett komplext tal $z=a+bi$ definieras absolutbeloppet $|z|$ som <br\><br\> | + | För de komplexa talen saknar man denna möjlighet. Vi kan inte utan vidare avgöra vilket tal som är störst av t.ex. $\,z=1-i\,$ och $\,w=-1+i\,$ . Med hjälp av begreppet <i>absolutbelopp</i> kan vi dock definiera ett mått på storleken av ett komplext tal. |
| - | <div class="regel">$$|z|=\sqrt{a^2+b^2}$$</div> | + | |
| - | Vi ser att $|z|$ är ett reellt tal och att $|z|\ge 0$. För reella tal $(b = 0)$ gäller att $|z|=\sqrt{a^2}=|a|$ , vilket överensstämmer med den vanliga definitionen för absolutbelopp av reella tal. | + | |
| - | Geometriskt är absolutbeloppet avståndet från talet $z=a+bi$ (punkten $(a, b)$) till $z = 0$ (origo), enligt Pythagoras sats.<br\> | + | För ett komplext tal $\,z=a+bi\,$ definieras absolutbeloppet $\,|z|\,$ som <br\><br\> |
| - | <div align="center">[[Bild:komplext-talplan-5.gif]]</div> | + | <div class="regel">$$|z|=\sqrt{a^2+b^2}\,\mbox{.}$$</div> |
| + | Vi ser att $\,|z|\,$ är ett reellt tal och att $\,|z|\ge 0\,$. För reella tal är $\,b = 0\,$ och då gäller att $\,|z|=\sqrt{a^2}=|a|\,$, vilket överensstämmer med den vanliga definitionen för absolutbelopp av reella tal. | ||
| + | Geometriskt är absolutbeloppet avståndet från talet $\,z=a+bi\,$ (punkten $\,(a, b)\,$) till $\,z = 0\,$ (origo), enligt Pythagoras sats.<br\> | ||
| + | <div align="center">[[Bild:komplext-talplan-5.gif||center|]]</div> | ||
| ==Avstånd mellan komplexa tal== | ==Avstånd mellan komplexa tal== | ||
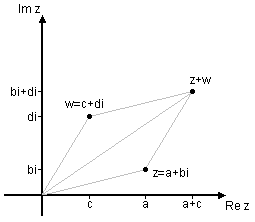
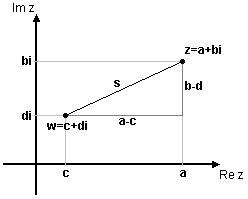
| - | Med hjälp av formeln för avstånd mellan punkter i ett koordinatsystem får man också en viktig och användbar tolkning av absolutbelopp. Avståndet $s$ mellan två komplexa tal $z=a+bi$ och $w=c+di$ <br>(se fig.) kan med hjälp av avståndsformeln skrivas <br\> | + | Med hjälp av formeln för avstånd mellan punkter i ett koordinatsystem får man också en viktig och användbar tolkning av absolutbelopp. Avståndet $\,s\,$ mellan två komplexa tal $\,z=a+bi\,$ och $\,w=c+di\,$ (se fig.) kan med hjälp av avståndsformeln skrivas <br\> |
| - | <div class="regel">$$s=\sqrt{(a-c)^2+(b-d)^2}$$</div> | + | <div class="regel">$$s=\sqrt{(a-c)^2+(b-d)^2}\,\mbox{.}$$</div> |
| - | <div align="center">[[Bild:komplext-talplan-6.gif]]</div><br> | + | [[Bild:komplext-talplan-6.gif||center|]]<br> |
| - | Eftersom $z-w=(a-c)+(b-d)i$, så får man att <br> | + | Eftersom $\,z-w=(a-c)+(b-d)i\,$, så får man att <br> |
| - | <div align="center">$|z-w|=\sqrt{(a-c)^2+(b-d)^2}=$ avståndet mellan talen $z$ och $w$.</div> | + | <center>$|z-w|=\sqrt{(a-c)^2+(b-d)^2}={}$avståndet mellan talen $\,z\,$ och $\,w\,$.</center> |
| + | |||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 3'''<br\> | + | '''Exempel 3'''<br/><br/> |
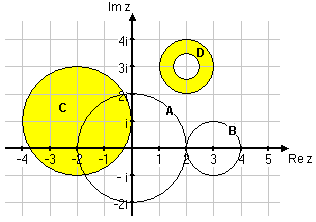
| - | Markera följande talmängder i det komplexa talplanet: <br\> | + | Markera följande talmängder i det komplexa talplanet: |
| - | <b>A: </b> $\,\, |z|=2$<br\> | + | <br/> |
| - | <b>B: </b> $\,\, |z-3|=1$<br\> | + | <br/> |
| - | <b>C: </b> $\,\, |z+2-i|\le 2$<br\> | + | <ol type="a"> |
| - | <b>D: </b> $\,\, \frac{1}{2}\le |z-(2+3i)|\le 1$<br\><br\> | + | <li>$\,\, |z|=2$ |
| - | <i>Lösning</i>:<br\> | + | <br/> |
| - | <b>A: </b> alla tal vars avstånd till origo är $2$. Dessa tal bildar i det komplexa talplanet en cirkel med radien 2 och medelpunkt i origo.<br\> | + | <br/> |
| - | <b>B: </b> alla tal vars avstånd till talet 3 är 1, dvs. en cirkel med radien 1 och medelpunkt i $z = 3$.<br\> | + | Ekvationen beskriver alla tal vars avstånd till origo är 2. Dessa tal bildar i det komplexa talplanet en cirkel med radien 2 och medelpunkt i origo.</li> |
| - | <b>C: </b> villkoret kan skrivas $|z-(-2+i)|$, vilket innebär alla tal på avståndet $\le 2$ från talet $-2+i$, dvs. en cirkelskiva med radien $2$ och medelpunkt i $-2+i$.<br\> | + | <br/> |
| - | <b>D: </b> alla tal vars avstånd till $z=2+3i$ är mellan $\frac{1}{2}$ och $1$.<br\><br\> | + | <li>$\,\, |z-3|=1$ |
| - | <div align="center">[[Bild:komplext-talplan-7.gif]]</div> | + | <br/> |
| + | <br/> | ||
| + | Denna ekvation uppfylls av alla tal vars avstånd till talet 3 är 1, dvs. en cirkel med radien 1 och medelpunkt i $\,z = 3\,$. | ||
| + | </li> | ||
| + | <br/> | ||
| + | <li>$\,\, |z+2-i|\le 2$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Vänsterledet kan skrivas $\,|z-(-2+i)|\,$, vilket innebär alla tal på avståndet ${}\le 2$ från talet $\,-2+i\,$, dvs. en cirkelskiva med radien 2 och medelpunkt i $\,-2+i\,$. | ||
| + | </li> | ||
| + | <br/> | ||
| + | <li>$\,\, \frac{1}{2}\le |z-(2+3i)|\le 1$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Mängden ges av alla tal vars avstånd till $\,z=2+3i\,$ är mellan $\,\frac{1}{2}\,$ och $\,1\,$. | ||
| + | <br/> | ||
| + | <br/> | ||
| + | </li> | ||
| + | </ol> | ||
| + | |||
| + | [[Bild:komplext-talplan-7.gif||center|]] | ||
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 4'''<br\> | '''Exempel 4'''<br\> | ||
| - | Markera i det komplexa talplanet alla tal $z$ som uppfyller villkoren | + | Markera i det komplexa talplanet alla tal $\,z\,$ som uppfyller villkoren |
| - | <table width="100%"> | + | <br/> |
| - | <tr> | + | <br/> |
| - | <td width="50%"> | + | <ol type="a"> |
| - | <ol type="a" start=1> | + | <li>$\, \left\{ \eqalign{&|z-2i|\le 3\cr &1\le\mathop{\rm Re} z\le 2}\right.$ |
| - | <li> $\, \left\{ \begin{matrix} |z-2i|\le 3 \\ 1\le\mbox{Re}\,z\le 2 \end{matrix} \right.$ | + | <br/> |
| + | <br/> | ||
| + | Den första olikheten ger punkterna på och innanför cirkeln med radie 3 och medelpunkt i $\,2i\,$. Den andra olikheten ger ett vertikalt band av punkter med realdel mellan 1 och 2. Det område som uppfyller båda olikheter ges av de punkter som ligger inom cirkeln och bandet. | ||
| + | </li> | ||
| + | <br/> | ||
| + | <li>$\, |z+1|=|z-2|$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Ekvationen kan skrivas $\,|z-(-1)|=|z-2|\,$. Man ser då att $\,z\,$ ska ligga på samma avstånd från $\,-1\,$ som från $\,2\,$. Detta villkor uppfylls av alla tal $\,z\,$ som har realdel $\,1/2\,$. | ||
| + | </li> | ||
| </ol> | </ol> | ||
| - | </td> | + | <br/> |
| - | <td width="50%"> | + | <br/> |
| - | <ol type="a" start=2> | + | <center>[[Bild:komplext-talplan-8.gif|Området i deluppgift a]][[Bild:komplext-talplan-10.gif|Området i deluppgift b]]</center> |
| - | <li> $\, |z+1|=|z-2|$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | <tr><td width="100%"><br><i>Lösning</i>:</td></tr> | + | |
| - | <tr> | + | |
| - | <td width="50%" valign="top"> | + | |
| - | <ol type="a" start=1> | + | |
| - | <li> <br\>[[Bild:komplext-talplan-8.gif]] | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | <td width="50%"> | + | |
| - | <ol type="a" start=2> | + | |
| - | <li> <br\> | + | |
| - | Ekvationen kan skrivas $|z-(-1)|=|z-2|$. Man ser då att $z$ ska ligga på samma avstånd från $-1$ som från $2$. Detta villkor uppfylls av alla tal z som har realdel $1/2$.[[Bild:komplext-talplan-10.gif]] | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| </div> | </div> | ||