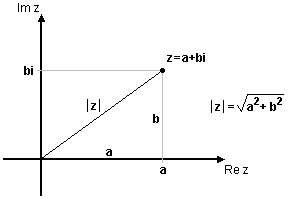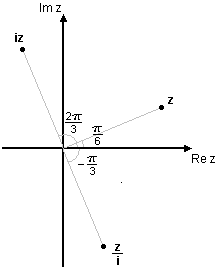3.2 Polär form
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 2 juli 2007 kl. 14.40 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) ← Gå till föregående ändring |
Versionen från 2 juli 2007 kl. 18.19 (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) Gå till nästa ändring → |
||
| Rad 157: | Rad 157: | ||
| ==Polär form== | ==Polär form== | ||
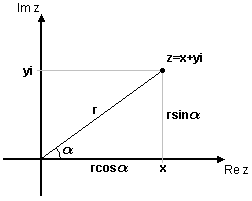
| - | I stället för att ange ett komplext tal $z=x+yi$ i dess rektangulära koordinater $(x, y)$ kan man använda polära koordinater. Detta innebär att man anger talets läge i det komplexa talplanet genom dess avstånd, $r$, till origo, samt den vinkel $\alpha$ som som bildas mellan den positiva $x$-axeln och sträckan från origo till talet (se fig.) | + | I stället för att ange ett komplext tal $\,z=x+iy\,$ i dess rektangulära koordinater $\,(x,y)\,$ kan man använda polära koordinater. Detta innebär att man anger talets läge i det komplexa talplanet genom dess avstånd, $\,r\,$, till origo, samt den vinkel $\,\alpha\,$ som som bildas mellan den positiva ''x''-axeln och sträckan från origo till talet (se figuren). |
| - | <div align="center">[[Bild:komplext-talplan-11.gif]]</div> | + | [[Bild:komplext-talplan-11.gif||center|]] |
| - | Eftersom $\quad \left\{ \begin{matrix} \cos\alpha = \displaystyle\frac{x}{r} \\ \mbox{ } \\ \sin\alpha = \displaystyle\frac{y}{r} \end{matrix} \right. \quad \Rightarrow \quad \left\{ \begin{matrix} x = r\cos\alpha \\ y= r\sin\alpha \end{matrix} \right. \quad$, så kan talet $z=x+yi$ skrivas | + | Eftersom $\ \cos\alpha = x/r\ $ och $\ \sin\alpha = y/r\ $ så är $\ x = r\cos\alpha\ $ och $\ y= r\sin\alpha\,$. Talet $\,z=x+iy\,$ kan därför skrivas som |
| - | <div class="regel">$$z=r\cos\alpha + ir\sin\alpha = r(\cos\alpha + i\sin\alpha)$$</div> | + | <div class="regel">$$z=r\cos\alpha + ir\sin\alpha = r(\cos\alpha + i\sin\alpha)\,\mbox{,}$$</div> |
| - | vilket kallas den <i>polära formen</i> av ett komplext tal $z$. Vinkeln $\alpha$ kallas <i>argumentet</i> för $z$ och skrivs | + | vilket kallas den <i>polära formen</i> av ett komplext tal $\,z\,$. Vinkeln $\,\alpha\,$ kallas <i>argumentet</i> för $\,z\,$ och skrivs |
| - | <div class="regel">$$\alpha=\arg\, z$$</div> | + | <div class="regel">$$\alpha=\arg z\,\mbox{.}$$</div> |
| - | Vinkeln $\alpha$ kan t.ex. bestämmas genom att lösa ekvationen $\tan\alpha=\displaystyle\frac{y}{x}$. Denna ekvation har dock flera lösningar, varför man måste se till att man väljer den lösning $\alpha$ som gör att $z= r(\cos\alpha + i\sin\alpha)$ hamnar i rätt kvadrant.<br\><br\> | + | Vinkeln $\,\alpha\,$ kan t.ex. bestämmas genom att lösa ekvationen $\,\tan\alpha=y/x\,$. Denna ekvation har dock flera lösningar, varför man måste se till att man väljer den lösning $\,\alpha\,$ som gör att $\,z= r(\cos\alpha + i\sin\alpha)\,$ hamnar i rätt kvadrant. |
| - | Det reella talet $r$, avståndet till origo, känner vi redan som beloppet av $z$, eftersom | + | |
| - | <div class="regel">$$r=\sqrt{x^2+y^2}=|z|$$</div> | + | |
| + | Det reella talet $\,r\,$, avståndet till origo, känner vi redan som beloppet av $\,z\,$, eftersom | ||
| + | <div class="regel">$$r=\sqrt{x^2+y^2}=|\,z\,|$$</div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 5'''<br\> | + | '''Exempel 5''' |
| + | <br/> | ||
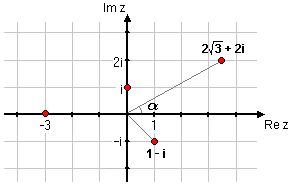
| Skriv följande komplexa tal på polär form: | Skriv följande komplexa tal på polär form: | ||
| - | <table width="100%"> | + | <ol type="a"> |
| - | <tr> | + | <li>$\,\,-3$ |
| - | <td width="45%"> | + | <br/> |
| - | <ol type="a" start=1> | + | <br/> |
| - | <li> $-3$ | + | Vi har att $\,|\,-3\,|=3\,$ och $\,\arg (-3)=\pi\,$, vilket betyder att $\,-3=3(\cos\pi+i\,\sin\pi)\,$. |
| + | </li> | ||
| + | <br/> | ||
| + | <li>$\,i$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Vi har att $\,|\,i\,|=1\,$ och $\,\arg i = \pi/2\,$ så i polär form är $\,i=\cos(\pi/2)+i\,\sin(\pi/2)\,$. | ||
| + | </li> | ||
| + | <br/> | ||
| + | <li>$\,1-i$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Formeln för beloppet av ett komplext tal ger att $\,|\,1-i\,|=\sqrt{1^2+(-1)^2}=\sqrt{2}\,$. Det komplexa talet ligger i den fjärde kvadranten och bildar vinkeln $\,\pi/4\,$ med den positiva reella axeln, vilket ger att $\,\arg (1-i)=2\pi-\pi/4=7\pi/4$. Alltså är $\,1-i=\sqrt{2}\,(\cos(7\pi/4)+i\sin(7\pi/4)\,)$. | ||
| + | </li> | ||
| + | <br/> | ||
| + | <li>$\,2\sqrt{3}+2i$ | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Beloppet är enklast att räkna ut | ||
| + | $$|\,2\sqrt{3}+2i\,|=\sqrt{(2\sqrt{3})^2+2^2}=\sqrt{16}=4\,\mbox{.}$$ | ||
| + | Om vi kallar argumentet för $\alpha$ så uppfyller det sambandet | ||
| + | $$\tan\alpha=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}$$ | ||
| + | och eftersom talet ligger i den första kvadranten (positiv real- och imaginärdel) så är $\,\alpha=\pi/6\,$ och vi har att | ||
| + | $$2\sqrt{3}+2i=4\bigl(\cos\frac{\pi}{6}+i\,\sin\frac{\pi}{6}\bigr)\,\mbox{.}$$ | ||
| + | </li> | ||
| + | <br/> | ||
| </ol> | </ol> | ||
| - | </td> | + | [[Bild:komplext-talplan-12.gif||center|]] |
| - | <td width="55%"> | + | |
| - | <ol type="a" start=2> | + | |
| - | <li> $i$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td width="45%"> | + | |
| - | <ol type="a" start=3> | + | |
| - | <li> $1-i$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | <td width="55%"> | + | |
| - | <ol type="a" start=4> | + | |
| - | <li> $2\sqrt3 +2i$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| - | <i>Lösning</i>: | + | |
| - | <table width="100%"> | + | |
| - | <tr> | + | |
| - | <td width="45%"> | + | |
| - | <ol type="a" start="1"> | + | |
| - | <li> $|-3|=3,\quad \arg(-3)=\pi$<br\> | + | |
| - | $-3=3(\cos\pi+i\sin\pi)$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | <td width="55%"> | + | |
| - | <ol type="a" start=2> | + | |
| - | <li> $|i|=1,\quad \arg\,i=\displaystyle\frac{\pi}{2}$<br\> | + | |
| - | $i=\displaystyle\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td width="45%"> | + | |
| - | <ol type="a" start=3> | + | |
| - | <li> $|1-i|=\sqrt{1^2+1^2}=\sqrt2$<br\> | + | |
| - | $ \arg(1-i)=\displaystyle\frac{7\pi}{4}$<br\> | + | |
| - | $1-i=\sqrt2\left(\displaystyle\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}\right)$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | <td width="55%"> | + | |
| - | <ol type="a" start=4> | + | |
| - | <li> $|2\sqrt3 +2i|=\sqrt{\left(2\sqrt3\right)^2 +2^2}=\sqrt{16}=4$<br\> | + | |
| - | $\arg\left(2\sqrt3 +2i\right)=\alpha$<br\> | + | |
| - | $\tan \alpha=\displaystyle\frac{2}{2\sqrt3}=\frac{1}{\sqrt3}\;\Rightarrow\;\alpha=\frac{\pi}{6}\; (+\pi n)$<br\> | + | |
| - | $2\sqrt3 +2i=4\left(\displaystyle\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\right)$<br\><br\> | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| - | <div align="center">[[Bild:komplext-talplan-12.gif]]</div> | + | |
| </div> | </div> | ||
| ==Multiplikation och division i polär form== | ==Multiplikation och division i polär form== | ||
| - | Den stora fördelen med att ha komplexa tal skrivna i polär form är att multiplikation och division då blir väldigt enkelt att utföra. För godtyckliga komplexa tal $z=|z|(\cos\alpha+i\sin\alpha)$ och $w=|w|(\cos\beta+i\sin\beta)$ kan man genom de trigonometriska additionsformlerna visa att | + | Den stora fördelen med att ha komplexa tal skrivna i polär form är att multiplikation och division då blir väldigt enkla att utföra. För godtyckliga komplexa tal $\,z=|z|(\cos\alpha+i\sin\alpha)\,$ och $\,w=|w|(\cos\beta+i\sin\beta)\,$ kan man genom de trigonometriska additionsformlerna visa att |
| <div class="regel"> | <div class="regel"> | ||
| - | $$z\cdot w=|z|\cdot |w|\left(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\right)$$ | + | $$\eqalign{z\cdot w&=|z|\cdot |w|\left(\cos(\alpha+\beta)+i\sin(\alpha+\beta)\right)\,\mbox{,}\cr \frac{z}{w}&=\frac{|z|}{|w|}\left(\cos(\alpha-\beta)+i\sin(\alpha-\beta)\right)\,\mbox{.}}$$ |
| - | $$\mbox{och}$$ | + | |
| - | $$\frac{z}{w}=\frac{|z|}{|w|}\left(\cos(\alpha-\beta)+i\sin(\alpha-\beta)\right)$$ | + | |
| </div> | </div> | ||
| Vid multiplikation av komplexa tal <i>multipliceras</i> alltså beloppen, medan argumenten <i>adderas</i>. | Vid multiplikation av komplexa tal <i>multipliceras</i> alltså beloppen, medan argumenten <i>adderas</i>. | ||
| Vid division av komplexa tal <i>divideras</i> beloppen och argumenten <i>subtraheras</i>. Detta kan kortfattat skrivas: | Vid division av komplexa tal <i>divideras</i> beloppen och argumenten <i>subtraheras</i>. Detta kan kortfattat skrivas: | ||
| <div class="regel"> | <div class="regel"> | ||
| - | $$|z\cdot w|=|z|\cdot |w|\quad \mbox{och}\quad \arg(z\cdot w)=\arg\,z + \arg\,w$$ | + | $$|z\cdot w|=|z|\cdot |w|\quad \mbox{och}\quad \arg(z\cdot w)=\arg\,z + \arg\,w\,\mbox{,}$$ |
| - | $$\left|\frac{z}{w}\right|=\frac{|z|}{|w|}\quad\quad\quad\; \mbox{ och}\quad \arg\left(\frac{z}{w}\right)=\arg\,z - \arg\,w$$ | + | $$\left|\frac{z}{w}\right|=\frac{|z|}{|w|}\quad\quad\quad\; \mbox{ och}\quad \arg\left(\frac{z}{w}\right)=\arg\,z - \arg\,w\,\mbox{.}$$ |
| </div> | </div> | ||
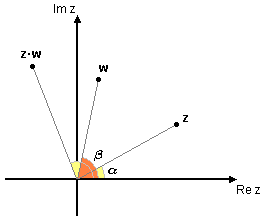
| - | I det komplexa talplanet innebär alltså en multiplikation av $z$ med $w$ att $z\;(|z|)$ förlängs med faktorn $|w|$ och roteras moturs med vinkeln $\arg\,w$. | + | I det komplexa talplanet innebär alltså en multiplikation av $\,z\,$ med $\,w\,$ att $\,z\,$ förlängs med faktorn $\,|w|\,$ och roteras moturs med vinkeln $\,\arg\,w\,$. |
| - | <div align="center">[[Bild:komplext-talplan-13.gif]]</div> | + | [[Bild:komplext-talplan-13.gif||center|]] |
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 6'''<br\> | + | '''Exempel 6''' |
| + | <br\> | ||
| Beräkna följande uttryck och genom att skriva om på polär form: | Beräkna följande uttryck och genom att skriva om på polär form: | ||
| <ol type="a"> | <ol type="a"> | ||
| - | <li> $\left( \displaystyle\frac{1}{\sqrt2} -\frac{1}{\sqrt2}i\right) \left/ \left( -\displaystyle\frac{1}{\sqrt2} +\frac{1}{\sqrt2}i\right) \right.$<br\><br\> | + | <li> $\Bigl(\displaystyle\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) \Big/ \Bigl( -\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr)$ |
| + | <br/> | ||
| + | <br/> | ||
| + | Vi skriver täljaren och nämnaren i polär form | ||
| + | $$\eqalign{\Bigl(\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) &= 1\cdot\Bigl(\cos\frac{7\pi}{4}+i\,\sin\frac{7\pi}{4}\Bigr)\cr \Bigr(-\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr) &= 1\cdot\Bigl(\cos\frac{3\pi}{4}+i\,\sin\frac{3\pi}{4}\Bigr)}$$ | ||
| + | och då följer att | ||
| + | $$\eqalign{&\Bigl(\frac{1}{\sqrt2} -\frac{i}{\sqrt2}\Bigr) \Big/ \Bigl(-\frac{1}{\sqrt2} +\frac{i}{\sqrt2}\Bigr) = \smash{\frac{\displaystyle\cos\frac{7}{4\pi}+i\,\sin\frac{7\pi}{4}\vphantom{\Biggl(}}{\displaystyle\cos\frac{3\pi}{4}+i\,\sin\frac{3\pi}{4}\vphantom{\Biggl)}}}\cr &\qquad\quad{}= \cos\Bigl(\frac{7\pi}{4}-\frac{3\pi}{4}\Bigl)+i\,\sin\Bigl(\frac{7\pi}{4}-\frac{3\pi}{4}\Bigr)= \cos\pi+i\,\sin\pi=-1\,\mbox{.}\vphantom{\Biggr)^{\Bigl(}}}$$ | ||
| + | </li> | ||
| + | <br/> | ||
| <li> $(-2-2i)(1+i)$ | <li> $(-2-2i)(1+i)$ | ||
| - | </ol> | + | <br/> |
| - | <i>Lösning</i>: | + | <br/> |
| - | <ol type="a"> | + | Faktorerna i uttrycket skriver vi i polär form |
| - | <li> $\displaystyle\left(\frac{1}{\sqrt2} -\frac{1}{\sqrt2}i\right) = 1\cdot\left(\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}\right)$ och $\displaystyle\left(-\frac{1}{\sqrt2} +\frac{1}{\sqrt2}i\right) = 1\cdot\left(\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4}\right)$ | + | $$\eqalign{(-2-2i)&=\sqrt8\Bigl(\cos\frac{5\pi}{4}+i\,\sin\frac{5\pi}{4}\Bigr)\,\mbox{,}\cr (1+i)&=\sqrt2\Bigl(\cos\frac{\pi}{4}+i\,\sin\frac{\pi}{4}\Bigr)\,\mbox{.}}$$ |
| - | <br\><br\> | + | Genom att utföra multiplikationen i polär form får vi att |
| - | $ \displaystyle \left(\frac{1}{\sqrt2} -\frac{1}{\sqrt2}i\right) \left/ \left(-\frac{1}{\sqrt2} +\frac{1}{\sqrt2}i\right) \right. = \displaystyle\frac{\displaystyle\cos\frac{7}{4\pi}+i\sin\frac{7\pi}{4}}{\displaystyle\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4}}=$ | + | $$\eqalign{(-2-2i)(1+i)&=\sqrt8 \cdot \sqrt2\,\Bigl(\cos\Bigl(\frac{5\pi}{4}+\frac{\pi}{4}\Bigr)+i\,\sin\Bigl(\frac{5\pi}{4}+\frac{\pi}{4}\Bigr)\Bigr)\cr &=4\cos\Bigl(\cos\frac{3\pi}{2}+i\,\sin\frac{3\pi}{2} \Bigr)=-4i\,\mbox{.}}$$ |
| - | <br\><br\> | + | </li> |
| - | $\displaystyle\cos\left(\frac{7\pi}{4}-\frac{3\pi}{4}\right)+i\sin\left(\frac{7\pi}{4}-\frac{3\pi}{4}\right)= \cos\pi+i\sin\pi=-1$ | + | <br/> |
| - | <br\><br\> | + | |
| - | <li> $\displaystyle(-2-2i)=\sqrt8\left(\cos\frac{5\pi}{4}+i\sin\frac{5\pi}{4}\right)\;$ och $\displaystyle(1+i)=\sqrt2\left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right)\;$ | + | |
| - | <br\><br\> | + | |
| - | $(-2-2i)(1+i)=\displaystyle\sqrt8 \cdot \sqrt2 \left(\cos\left(\frac{5\pi}{4}+\frac{\pi}{4}\right)+i\sin\left(\frac{5\pi}{4}+\frac{\pi}{4}\right)\right)=$ | + | |
| - | <br\><br\> | + | |
| - | $\displaystyle 4\cos\left(\cos\frac{3\pi}{4}+i\sin\frac{3\pi}{4} \right)=-4i$ | + | |
| </ol> | </ol> | ||
| </div> | </div> | ||
| <div class="exempel"> | <div class="exempel"> | ||
| - | '''Exempel 7'''<br\> | + | '''Exempel 7''' |
| - | Beräkna $iz$ och $\displaystyle\frac{z}{i}$ om | + | <br\> |
| + | |||
| <ol type="a"> | <ol type="a"> | ||
| - | <li> $\displaystyle z=2\left(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\right)$<br\><br\> | + | <li>Beräkna $\,iz\,$ och $\,\displaystyle\frac{z}{i}\,$ om $\ \displaystyle z=2\Bigl(\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}\Bigr)\,$. Svara på polär form. |
| - | <li> $\displaystyle z=3\left(\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}\right)$ | + | <br/> |
| + | <br/> | ||
| + | Eftersom $\ \displaystyle i=1\cdot \left(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\right)\ $ så är | ||
| + | $$\eqalign{iz&=2\Bigl(\cos\Bigl(\frac{\pi}{6}+\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{\pi}{6}+\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}\Bigr)\cr \frac{i}{z}&=2\Bigl(\cos\Bigl(\frac{\pi}{6}-\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{\pi}{6}-\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{-\pi}{3}+i\,\sin\frac{-\pi}{3}\Bigr)}$$ | ||
| + | </li> | ||
| + | <br/> | ||
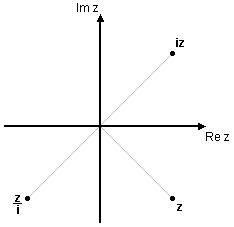
| + | <li> Beräkna $iz$ och $\displaystyle\frac{z}{i}$ om $\displaystyle z=3\left(\cos\frac{7\pi}{4}+i\sin\frac{7\pi}{4}\right)\,$. Svara på polär form. | ||
| + | <br/> | ||
| + | <br/> | ||
| + | Använder vi den polära formen av $\,i\,$ så fås att | ||
| + | $$\eqalign{iz&=3\Bigl(\cos\Bigl(\frac{7\pi}{4}+\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{7\pi}{4}+\frac{\pi}{2}\Bigr)\,\Bigr) =3\Bigl(\cos\frac{9\pi}{4}+i\sin\frac{9\pi}{4}\Bigr)\cr &=3\left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right)\cr \frac{i}{z}&=2\Bigl(\cos\Bigl(\frac{7\pi}{4}-\frac{\pi}{2}\Bigr)+i\,\sin\Bigl(\frac{7\pi}{4}-\frac{\pi}{2}\Bigr)\,\Bigr)= 2\Bigl(\cos\frac{5\pi}{4}+i\,\sin\frac{5\pi}{4}\Bigr)}$$ | ||
| + | </li> | ||
| + | <br/> | ||
| </ol> | </ol> | ||
| - | Svara på polär form.<br\> | + | Vi ser här att multiplikation med $\,i\,$ innebär en rotation $\,\pi/2\,$ moturs, medan division med $\,i\,$ medför en rotation $\,\pi/2\,$ medurs. |
| - | <i>Lösning</i>: | + | <center>[[Bild:komplext-talplan-14.gif|Deluppgift a]][[Bild:komplext-talplan-15.gif|Deluppgift b]]</center> |
| - | <table width="100%"> | + | |
| - | <tr> | + | |
| - | <td width="70%"> | + | |
| - | <ol type="a" start=1> | + | |
| - | <li> $\displaystyle i=1\cdot \left(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\right)$ | + | |
| - | $\displaystyle iz=2\left(\cos\left(\frac{\pi}{6}+\frac{\pi}{2}\right)+i\sin\left(\frac{\pi}{6}+\frac{\pi}{2}\right)\right)= 2\left(\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}\right)$<br\><br\> | + | |
| - | $\displaystyle \frac{i}{z}=2\left(\cos\left(\frac{\pi}{6}-\frac{\pi}{2}\right)+i\sin\left(\frac{\pi}{6}-\frac{\pi}{2}\right)\right)= 2\left(\cos\frac{-\pi}{3}+i\sin\frac{-\pi}{3}\right)$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | <td width="30%> | + | |
| - | [[Bild:komplext-talplan-14.gif]] | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td width="70%"> | + | |
| - | <ol type="a" start=2> | + | |
| - | <li> $\displaystyle iz=3\left(\cos\left(\frac{7\pi}{4}+\frac{\pi}{2}\right)+i\sin\left(\frac{7\pi}{4}+\frac{\pi}{2}\right)\right)=$ <br><br>$\displaystyle 3\left(\cos\frac{9\pi}{4}+i\sin\frac{9\pi}{4}\right)= 3\left(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}\right)$<br\><br\> | + | |
| - | $\displaystyle \frac{i}{z}=2\left(\cos\left(\frac{7\pi}{4}-\frac{\pi}{2}\right)+i\sin\left(\frac{7\pi}{4}-\frac{\pi}{2}\right)\right)= 2\left(\cos\frac{5\pi}{4}+i\sin\frac{5\pi}{4}\right)$ | + | |
| - | </ol> | + | |
| - | </td> | + | |
| - | <td width="30%> | + | |
| - | [[Bild:komplext-talplan-15.gif]] | + | |
| - | </td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| - | Vi ser här att multiplikation med i innebär en rotation $\displaystyle\frac{\pi}{2}$ moturs, medan division med $i$ medför en rotation $\displaystyle\frac{\pi}{2}$ medurs. | + | |
| </div> | </div> | ||