2.2 Variabelsubstitution
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 27 april 2007 kl. 15.00 (redigera) Lina (Diskussion | bidrag) (→Variabelsubstitution) ← Gå till föregående ändring |
Versionen från 27 april 2007 kl. 15.07 (redigera) (ogör) Lina (Diskussion | bidrag) (→Integrationsgränser vid variabelbyte) Gå till nästa ändring → |
||
| Rad 110: | Rad 110: | ||
| Alternativt ändrar man integrationsgränser samtidigt som man gör variabelbytet. | Alternativt ändrar man integrationsgränser samtidigt som man gör variabelbytet. | ||
| De båda metoderna illustreras i följande exempel. | De båda metoderna illustreras i följande exempel. | ||
| + | |||
| <div class="exempel"> | <div class="exempel"> | ||
| Rad 143: | Rad 144: | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
| + | [[Bild:Integral20.gif|200px|right]] | ||
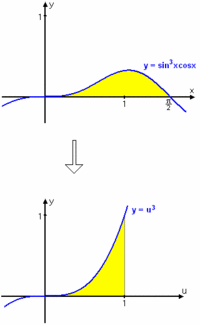
| Beräkna integralen $ \quad \displaystyle \int_{0}^{\frac{x}{2}} \sin^3 x \cos x \, dx$. | Beräkna integralen $ \quad \displaystyle \int_{0}^{\frac{x}{2}} \sin^3 x \cos x \, dx$. | ||
| - | |||
| - | |||
| - | \\illustration | ||
| Rad 157: | Rad 156: | ||
| $\displaystyle \int_{0}^{\frac{x}{2}} \sin^3 x \cos x \, dx= \displaystyle \int_{0}^{1} u^3 du = \left[ \displaystyle \frac{u^4}{4} \right]_{0}^{1} = \displaystyle \frac{1}{4} - 0 = \displaystyle \frac{1}{4}$ | $\displaystyle \int_{0}^{\frac{x}{2}} \sin^3 x \cos x \, dx= \displaystyle \int_{0}^{1} u^3 du = \left[ \displaystyle \frac{u^4}{4} \right]_{0}^{1} = \displaystyle \frac{1}{4} - 0 = \displaystyle \frac{1}{4}$ | ||
| + | |||
| + | |||
| (Figuren till höger visar vad som händer vid variabelbytet; integrand och variabel ändras. Integralens värde, storleken på arean, ändras dock inte.) | (Figuren till höger visar vad som händer vid variabelbytet; integrand och variabel ändras. Integralens värde, storleken på arean, ändras dock inte.) | ||
| Rad 169: | Rad 170: | ||
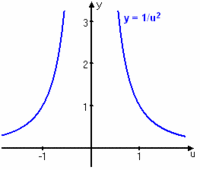
| $\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{ \cos x} {\sin^2 x} dx = \left[ \matrix{ u = \sin x \\ du = \cos x \, dx \\ u(- \frac{\pi}{2}) = -1 \\ u (\frac{\pi}{2}) = 1} \right ] = \displaystyle \int_{-1}^{1} \displaystyle \frac{1}{u^2} \, du = \left[ -\displaystyle \frac{1}{u} \right]_{0}^{1} = -1 - 1 = -2$ | $\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{ \cos x} {\sin^2 x} dx = \left[ \matrix{ u = \sin x \\ du = \cos x \, dx \\ u(- \frac{\pi}{2}) = -1 \\ u (\frac{\pi}{2}) = 1} \right ] = \displaystyle \int_{-1}^{1} \displaystyle \frac{1}{u^2} \, du = \left[ -\displaystyle \frac{1}{u} \right]_{0}^{1} = -1 - 1 = -2$ | ||
| + | [[Bild:Integral21.gif|200px|right]] | ||
| Denna uträkning är dock felaktig, vilket beror på | Denna uträkning är dock felaktig, vilket beror på | ||
| - | att $f(u)= \displaystyle \frac{1}{u^2}$ inte är kontinuerlig i intervallet $[-1, 1]$ (se fig.). \\illustration<br> | + | att $f(u)= \displaystyle \frac{1}{u^2}$ inte är kontinuerlig i intervallet $[-1, 1]$ (se fig.). |
| + | |||
| Villkoret att $f(u(x))$ ska vara definierad och kontinuerlig för alla värden som $u(x)$ kan anta i det | Villkoret att $f(u(x))$ ska vara definierad och kontinuerlig för alla värden som $u(x)$ kan anta i det | ||
| aktuella intervallet är alltså nödvändigt för att | aktuella intervallet är alltså nödvändigt för att | ||
| substitutionen $u=u(x)$ ska fungera. | substitutionen $u=u(x)$ ska fungera. | ||
| + | |||
| + | |||
| + | |||
| </div> | </div> | ||