1.3 Max- och minproblem
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 14 juni 2007 kl. 17.53 (redigera) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst (delvis)) ← Gå till föregående ändring |
Versionen från 15 juni 2007 kl. 07.37 (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) (Korrekturläst) Gå till nästa ändring → |
||
| Rad 324: | Rad 324: | ||
| De kritiska punkterna till funktionen ges av | De kritiska punkterna till funktionen ges av | ||
| - | $$\displaystyle y'=0 \quad \Leftrightarrow \quad 1= \frac {2}{3} \cdot \frac{1}{\sqrt[3]{x}}\quad\Leftrightarrow\quad \sqrt[3]{x} = {\textstyle\frac {2}{3}} \quad \Leftrightarrow \quad x = \bigl({\textstyle\frac{2}{3}}\bigr)^3 = \frac{8}{27}\,\mbox{.}$$ | + | $$\displaystyle y'=0 \quad \Leftrightarrow \quad 1= \frac {2}{3} \cdot \frac{1}{\sqrt[3]{x}}\quad\Leftrightarrow\quad \sqrt[3]{x} = {\textstyle\frac {2}{3}} \quad \Leftrightarrow \quad x = \bigl({\textstyle\frac{2}{3}}\bigr)^3 = {\textstyle\frac{8}{27}}\,\mbox{.}$$ |
| - | + | De enda punkter där funktionen eventuellt kan ha extrempunkter är alltså $\,x=0\,$ och $\,x=\frac{8}{27}\,$. För att avgöra dessa punkters karaktär skriver vi upp en teckentabell: | |
| - | Teckentabell: | + | |
| {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | {| BORDER="1" CELLPADDING="5" CELLSPACING="0" ALIGN="center" | ||
| |- | |- | ||
| - | |width= "50" ALIGN="center"| $x$ | + | |width="50px" align="center" style="background:#efefef;"| $x$ |
| - | | | + | |width="50px" align="center" style="background:#efefef;"| |
| - | |ALIGN="center"| $0$ | + | |width="50px" align="center" style="background:#efefef;"| $0$ |
| - | | | + | |width="50px" align="center" style="background:#efefef;"| |
| - | |ALIGN="center"| $\frac{8}{27}$ | + | |width="50px" align="center" style="background:#efefef;"| $\frac{8}{27}$ |
| - | | | + | |width="50px" align="center" style="background:#efefef;"| |
| |- | |- | ||
| - | |width= "50" ALIGN="center"| $y'$ | + | |width="50px" align="center"| $y'$ |
| - | |width= "50" ALIGN="center"| $+$ | + | |width="50px" align="center"| $+$ |
| - | |width= "50" ALIGN="center"| $ ej def.$ | + | |width="50px" align="center"| ej def. |
| - | |width= "50" ALIGN="center"| $-$ | + | |width="50px" align="center"| $-$ |
| - | |width= "50" ALIGN="center"| $0$ | + | |width="50px" align="center"| $0$ |
| - | |width= "50" ALIGN="center"| $+$ | + | |width="50px" align="center"| $+$ |
| |- | |- | ||
| - | |ALIGN="center"| $y$ | + | |width="50px" align="center"| $y$ |
| - | |ALIGN="center"|$\nearrow$ | + | |width="50px" align="center"| $\nearrow$ |
| - | |ALIGN="center"| | + | |width="50px" align="center"| $0$ |
| - | |ALIGN="center"| $\searrow$ | + | |width="50px" align="center"| $\searrow$ |
| - | |ALIGN="center"| $\rightarrow$ | + | |width="50px" align="center"| $-\frac{4}{27}$ |
| - | |ALIGN="center"| $\nearrow$ | + | |width="50px" align="center"| $\nearrow$ |
| |} | |} | ||
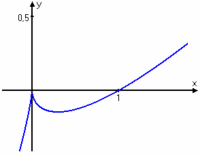
| + | Kurvan har alltså en lokal maximipunkt i $\,(0, 0)\,$ (en spets) och en lokal minimipunkt i $\,(\frac{8}{27},-\frac{4}{27})\,$. | ||
| - | {| | + | [[Bild:X-xu23.gif|200px|center|]] |
| - | |- | + | |
| - | | width=45% valign=top | | + | |
| - | $y(0)=0$ | + | |
| - | + | ||
| - | $y(\frac{8}{27}) = -\frac{4}{27}$ | + | |
| - | | width=50% valign=top | | + | |
| - | [[Bild:X-xu23.gif|200px|right|]] | + | |
| - | | width=5% valign=top | | + | |
| - | + | ||
| - | |} | + | |
| - | + | ||
| - | + | ||
| - | Kurvan har alltså en max-punkt i $(0, 0)$ (en spets) och en min-punkt i $( \frac{8}{27} , -\frac{4}{27})$. | + | |
| </div> | </div> | ||
| Rad 395: | Rad 382: | ||
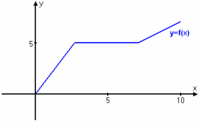
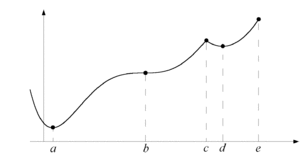
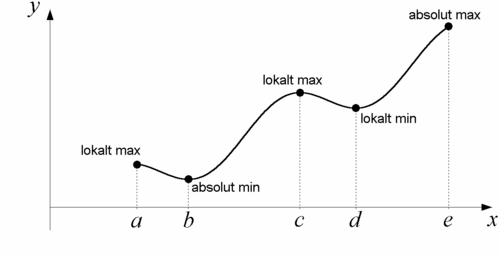
| Funktionen ovan betraktas endast i intervallet $a\le x \le e$. | Funktionen ovan betraktas endast i intervallet $a\le x \le e$. | ||
| - | Vi ser att funktionens minsta värde i detta intervall inträffar i $x=b$ , medan största värdet återfinns i ändpunkten $x=e$. | + | Vi ser att funktionens minsta värde i detta intervall inträffar i den kritiska punkten $x=b$ , medan största värdet återfinns i ändpunkten $x=e$. |
| Rad 401: | Rad 388: | ||
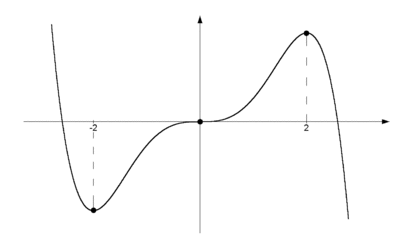
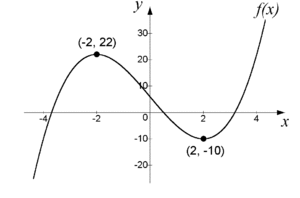
| '''Exempel 7''' | '''Exempel 7''' | ||
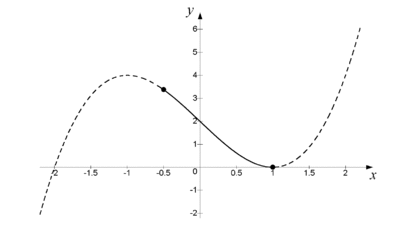
| - | Bestäm största och minsta värde för funktionen $f(x) = x^3 -3x + 2$ i intervallet $-0{,}5 \le x \le 1$. | + | Bestäm största och minsta värde för funktionen $\,f(x) = x^3 -3x + 2\,$ i intervallet $\,-0{,}5 \le x \le 1\,$. |
| - | + | <br> | |
| - | + | <br> | |
| - | '''Lösning''' | + | Vi deriverar funktionen $\,f^{\,\prime}(x) = 3x^2 -3\,$ och sätter derivatan lika med noll för att få fram alla kritiska punkter |
| - | + | $$f^{\,\prime}(x) = 0 \quad \Leftrightarrow \quad x^2 = 1 \quad \Leftrightarrow \quad x= \pm 1\,\mbox{.}$$ | |
| - | $f'(x) = 3x^2 -3$ | + | Punkten $x = –1$ ligger dock utanför den aktuella definitionsmängden och $x = 1$ sammanfaller med definitionsmängdens ena ändpunkt. Eftersom funktionen saknar singulära punkten (funktioen är deriverbar överallt) måste funktionens största och minsta värde antas i intervallets ändpunkter. |
| - | + | $$\eqalign{f(-0{,}5) &= 3{,}375\cr f(1)&=0}$$ | |
| - | $f'(x) = 0 \quad \rightarrow \quad x^2 = 1 \quad \rightarrow \quad x= \pm 1 $ | + | |
| - | + | ||
| - | + | ||
| - | $x = –1$ ligger dock utanför den aktuella definitionsmängden och $x = 1$ sammanfaller med definitionsmängdens ena ändpunkt, varför största och minsta värde för $f(x)$ måste finnas i intervallets ändpunkter. | + | |
| - | + | ||
| - | + | ||
| - | $f(-0{,}5) = 3{,}375$ | + | |
| - | + | ||
| - | $f(1)=0$ | + | |
| - | + | ||
| - | + | ||
| Funktionens största värde i det givna intervallet är alltså $3{,}375$. Minsta värdet är $0$ (se fig.) | Funktionens största värde i det givna intervallet är alltså $3{,}375$. Minsta värdet är $0$ (se fig.) | ||
| Rad 428: | Rad 404: | ||
| ==Andraderivatan== | ==Andraderivatan== | ||
| - | Tecknet på derivatan av en funktion ger oss information om huruvida funktionen är växande eller avtagande. På samma sätt kan andraderivatans tecken visa om förstaderivatan är växande eller avtagande. Detta kan man bl.a. utnyttja för att ta reda på om en given extrempunkt är en max-, eller min-punkt. | + | Tecknet på derivatan av en funktion ger oss information om huruvida funktionen är växande eller avtagande. På samma sätt kan andraderivatans tecken visa om förstaderivatan är växande eller avtagande. Detta kan man bl.a. utnyttja för att ta reda på om en given extrempunkt är en max-, eller minpunkt. |
| - | Om $f(x)$ har en max-punkt, där $f'(x)=0$ : | ||
| - | {| | ||
| - | |- | ||
| - | | width=50% valign=top | | ||
| - | {| class="wikitable" cellpadding="4px" cellspacing="0px" width="100%" | ||
| - | |- | ||
| - | |width="30" style="text-align:right;"| $\rightarrow$ | ||
| - | |style="text-align:left" | kurvans lutning, $f'(x)$ , är avtagande | ||
| - | |- | ||
| - | | | ||
| - | |(från positiv lutning till negativ lutning) | ||
| - | |- | ||
| - | |width="30" style="text-align:right;"| $\rightarrow$ | ||
| - | |style="text-align:left" | derivatan av $f'(x)$ är negativ | ||
| - | |- | ||
| - | |width="30" style="text-align:right;"| $\rightarrow$ | ||
| - | |style="text-align:left" | $f{'}{'}(x) < 0$ | ||
| - | |} | ||
| - | | width=45% valign=top | | ||
| - | [[Bild:Fmax.gif|200px]] | ||
| - | | width=5% valign=top | | ||
| - | |} | ||
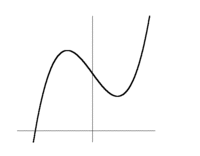
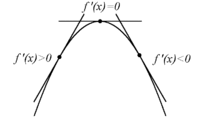
| - | Om $f(x)$ har en min-punkt, där $f'(x)= 0$: | + | [[Bild:Fmax.gif|200px|right]] |
| - | {| | + | Om funktionen $\,f(x)\,$ har en kritisk punkt i $\,x=a\,$ där $f^{\,\prime\prime}(a)<0$, då gäller att |
| - | |- | + | :# Derivatan $\,f^{\,\prime}(x)\,$ är strängt avtagande i en omgivning kring $\,x=a\,$. |
| - | | width=50% valign=top | | + | :# Eftersom $\,f^{\,\prime}(a)=0\,$ är alltså $\,f^{\,\prime}(x)>0\,$ till vänster om $\,x=a\,$ och $\,f^{\,\prime}(x)<0\,$ till höger om $\,x=a\,$. |
| - | {| class="wikitable" cellpadding="4px" cellspacing="0px" width="100%" | + | :# Detta medför att funktionen $\,f(x)\,$ har en lokal maximipunkt i $\,x=a\,$. |
| - | |- | + | |
| - | |width="30" style="text-align:right;"| $\rightarrow$ | + | |
| - | |style="text-align:left" | kurvans lutning, $f'(x)$, är växande | + | |
| - | |- | + | |
| - | | | + | |
| - | |(från negativ lutning till positiv lutning) | + | |
| - | |- | + | |
| - | |width="30" style="text-align:right;"| $\rightarrow$ | + | |
| - | |style="text-align:left" | derivatan av $f'(x)$ är positiv | + | |
| - | |- | + | |
| - | |width="30" style="text-align:right;"| $\rightarrow$ | + | |
| - | |style="text-align:left" | $f{'}{'}(x) > 0$ | + | |
| - | |} | + | |
| - | | width=45% valign=top | | + | |
| - | [[Bild:Fmin.gif|200px]] | + | |
| - | | width=5% valign=top | | + | |
| - | |} | + | |
| - | Om $f{'}{'}(x)=0$, får vi ingen information utan ytterligare undersökning krävs, t.ex. teckentabell. | ||
| + | [[Bild:Fmin.gif|200px|right]] | ||
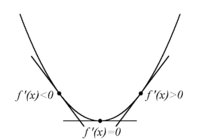
| + | Om funktionen $\,f(x)\,$ har en kritisk punkt i $\,x=a\,$ där $f^{\,\prime\prime}(a)>0$, då gäller att | ||
| + | :# Derivatan $\,f^{\,\prime}(x)\,$ är strängt växande i en omgivning kring $\,x=a\,$. | ||
| + | :# Eftersom $\,f^{\,\prime}(a)=0\,$ är alltså $\,f^{\,\prime}(x)<0\,$ till vänster om $\,x=a\,$ och $\,f^{\,\prime}(x)>0\,$ till höger om $\,x=a\,$. | ||
| + | :# Detta medför att funktionen $\,f(x)\,$ har en lokal minimipunkt i $\,x=a\,$. | ||
| - | <div class="exempel"> | ||
| - | '''Exempel 8''' | ||
| - | Bestäm alla extrempunkter för funktionen $f(x)=x^3 -x^2 -x +2$ och bestäm deras karaktär med hjälp av andraderivatan. | + | Om $\,f^{\,\prime\prime}(a)=0$, får vi ingen information utan ytterligare undersökning krävs, t.ex. teckentabell. |
| - | '''Lösning''' | + | <div class="exempel"> |
| - | + | '''Exempel 8''' | |
| - | $f'(x) = 3x^2 -2x - 1$ | + | |
| - | + | ||
| - | $f'(x) = 0 \quad \rightarrow \quad x^2 - \displaystyle \frac{2}{3} x - \frac{1}{3} = 0 \quad \rightarrow \quad x=1 \quad eller \quad x = -\displaystyle \frac{1}{3}$ | + | |
| - | + | ||
| - | $f(x)$ har extrempunkter då $x = 1$ och $x=-\displaystyle \frac{1}{3}$. | + | |
| - | + | ||
| - | + | ||
| - | Andraderivatans tecken ger vilken typ: | + | |
| - | + | ||
| - | $f{'}{'}(x) = 6x - 2$ | + | |
| - | $f{'}{'}(-\displaystyle \frac{1}{3}) = -4 < 0 \quad \rightarrow \quad f_{max} \mbox{ då} x = -\displaystyle \frac{1}{3}$. | + | Bestäm alla extrempunkter för funktionen $\,f(x)=x^3 -x^2 -x +2\,$ och bestäm deras karaktär med hjälp av andraderivatan. |
| - | + | <br> | |
| - | $f{'}{'}(1) = 4 > 0 \quad \rightarrow \quad f_{min} \mbox{ då} x = 1$. | + | <br> |
| + | Funktionen är ett polynom och är därför deriverbar överallt. Om funktionen har några extrempunkter så måste de därför finnas bland de kritiska punkterna. Vi deriverar därmed funktionen, $\,f^{\,\prime}(x) = 3x^2 -2x - 1\,$, och sätter derivatan lika med noll | ||
| + | $$f^{\,\prime}(x) = 0 \quad \Leftrightarrow \quad x^2 - \frac{2}{3} x - \frac{1}{3} = 0 \quad \Leftrightarrow \quad x=1 \quad\text{eller}\quad x = -\frac{1}{3}\,\mbox{.}$$ | ||
| + | Funktionen har kritiska punkter i $x = 1$ och $x=-\frac{1}{3}$. Med hjälp av tecknet på andraderivatan $\,f^{\,\prime\prime}(x)=6x-2\,$ kan vi bestämma vilken typ av extrempunkt respektive kritisk punkt är. | ||
| + | :*För $\,x=-\frac{1}{3}\,$ har vi att $\,f^{\,\prime\prime}(-\frac{1}{3})=-4<0\,$ och det betyder att $\,x=-\frac{1}{3}\,$ är en lokal maximipunkt. | ||
| + | :*För $\,x=1\,$ har vi att $\,f^{\,\prime\prime}(1)=4>0\,$ och det betyder att $\,x=1\,$ är en lokal minimipunkt. | ||
| </div> | </div> | ||