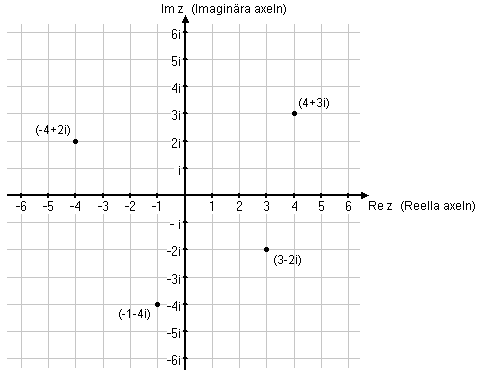3.2 Polär form
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 18 juni 2007 kl. 09.01 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Det komplexa talplanet) ← Gå till föregående ändring |
Versionen från 18 juni 2007 kl. 09.05 (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Det komplexa talplanet) Gå till nästa ändring → |
||
| Rad 36: | Rad 36: | ||
| Man bildar därför ett koordinatsystem genom att ställa en imaginär axel (en tallinje med enheten $i$) vinkelrät mot en reell axel (den reella tallinjen). Vi kan nu beskriva varje komplext tal med en punkt i detta koordinatsystem, och varje punkt beskriver ett unikt komplext tal. | Man bildar därför ett koordinatsystem genom att ställa en imaginär axel (en tallinje med enheten $i$) vinkelrät mot en reell axel (den reella tallinjen). Vi kan nu beskriva varje komplext tal med en punkt i detta koordinatsystem, och varje punkt beskriver ett unikt komplext tal. | ||
| <div align="center">[[Bild:komplext-talplan-1.gif]]</div> | <div align="center">[[Bild:komplext-talplan-1.gif]]</div> | ||
| + | <br\> | ||
| + | |||
| + | Denna geometriska tolkning av de komplexa talen kallas det <i>komplexa talplanet</i>.<br\> | ||
| + | Anm: | ||
| + | De reella talen, dvs. alla komplexa tal med imaginärdel $= 0$, ligger alltså längs den reella axeln. Man kan alltså se utvidgningen av talsystemet från \mathbb{R} (de reella talen) till \mathbb{Z} (de komplexa talen) som att tillföra en ny dimension till den redan fyllda tallinjen. | ||
| + | <br\><br\> | ||
| + | Addition av komplexa tal får helt naturligt en enkel tolkning i det komplexa talplanet och sker geometriskt på samma sätt som vid addition av vektorer: | ||
| ==Förlängning och förkortning== | ==Förlängning och förkortning== | ||