Teori
Det komplexa talplanet
Eftersom ett komplext tal $\,z=a+bi\,$ består av en realdel $(a)$ och en imaginärdel $(b)$, så kan $z$ betraktas som ett ordnat talpar $(a, b)$ och tolkas som en punkt i ett koordinatsystem.
Man bildar därför ett koordinatsystem genom att ställa en imaginär axel (en tallinje med enheten $i$) vinkelrät mot en reell axel (den reella tallinjen). Vi kan nu beskriva varje komplext tal med en punkt i detta koordinatsystem, och varje punkt beskriver ett unikt komplext tal.
Denna geometriska tolkning av de komplexa talen kallas det komplexa talplanet.
Anm:
De reella talen, dvs. alla komplexa tal med imaginärdel $= 0$, ligger alltså längs den reella axeln. Man kan alltså se utvidgningen av talsystemet från $\displaystyle\mathbb{R}$ (de reella talen) till $\mathbb{Z}$ (de komplexa talen) som att tillföra en ny dimension till den redan fyllda tallinjen.
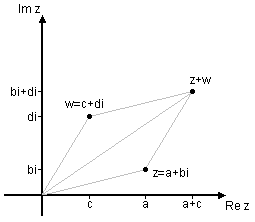
Addition av komplexa tal får helt naturligt en enkel tolkning i det komplexa talplanet och sker geometriskt på samma sätt som vid addition av vektorer:
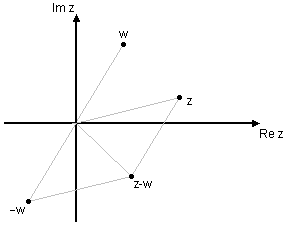
Subtraktion kan ses som addition av motsvarande negativa tal, dvs. $z-w=z+(-w)$ och får följande utseende:
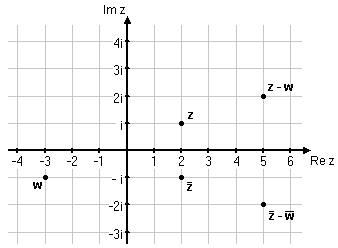
Exempel 1
$z=2+i,\quad w=-3-i$
Markera $z,\, w,\, \bar z, \,\bar z -\bar w\,$ och $\,z- w\,$ i det komplexa talplanet.
Lösning:
$\bar z=2-i$
$\bar w=-3+i$
$z-w=2+i-(-3-i)=5+2i$
$\bar z -\bar w = 2-i -(-3+i)=5-2i\quad (=\bar{z-w})$
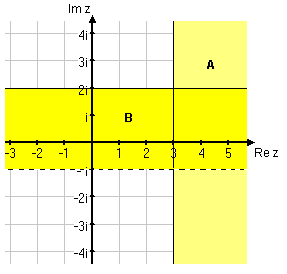
Exempel 2
Markera i det komplexa talplanet alla tal $z$ som uppfyller följande villkor:
A: $\mbox{Re} \, z \ge 3$
B: -1 < $\mbox{Im} \, z \le 2$
Lösning:
Förlängning och förkortning
teori
$$ fristående formel dubbla dollar $$
teori igen
Tips:
å här är världens tips asså
teori, vad skulle vi göra utan det
Viktig regel:
$$dubbeldollar$$
Exempel 1
Exempeltext, använd nedanstående numrering
- $matte$
- text
teori igen
Råd för inläsning
Tänk på att:
text
Lästips
stående
Länktips
stående
© Copyright 2007, math.se
|