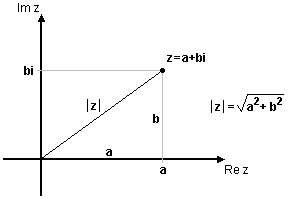3.2 Polär form
Sommarmatte 2
(Skillnad mellan versioner)
| Versionen från 18 juni 2007 kl. 10.15 (redigera) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Det komplexa talplanet) ← Gå till föregående ändring |
Versionen från 18 juni 2007 kl. 10.22 (redigera) (ogör) KTH.SE:u1zpa8nw (Diskussion | bidrag) (→Absolutbelopp) Gå till nästa ändring → |
||
| Rad 73: | Rad 73: | ||
| ==Absolutbelopp== | ==Absolutbelopp== | ||
| + | De reella talen går att ordna i storleksordning, dvs. vi kan avgöra om ett reellt tal är större än ett annat; ju längre till höger på den reella tallinjen desto större är talet. <br\> | ||
| + | För de komplexa talen saknar man denna möjlighet. Vi kan inte utan vidare avgöra vilket tal som är störst av t.ex. $z=1-i$ och $w=-1+i$ . Med hjälp av begreppet <i>absolutbelopp</i> kan vi dock definiera ett mått på storleken av ett komplext tal.<br\><br\> | ||
| + | För ett komplext tal $z=a+bi$ definieras absolutbeloppet $|z|$ som <br\><br\> | ||
| + | $$|z|=\sqrt{a^2+b^2}$$<br\><br\> | ||
| + | Vi ser att $|z|$ är ett reellt tal och att $|z|\ge 0$. För reella tal $(b = 0)$ gäller att $|z|=\sqrt{a^2}=|a|$ , vilket överensstämmer med den vanliga definitionen för absolutbelopp av reella tal. | ||
| + | Geometriskt är absolutbeloppet avståndet från talet $z=a+bi$ (punkten $(a, b)$) till $z = 0$ (origo), enligt Pythagoras sats.<br\> | ||
| + | <div align="center">[[Bild:komplext-talplan-5.gif]]</div> | ||
| ==Förlängning och förkortning== | ==Förlängning och förkortning== | ||