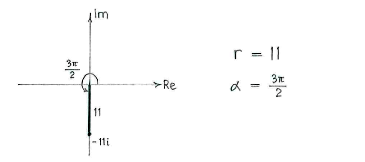From Förberedande kurs i matematik 2

Revision as of 08:10, 21 August 2008 (edit) Tekbot (Talk | contribs) m (Robot: Automated text replacement (-[[Bild: +[[Image:)) ← Previous diff		Current revision (13:14, 29 October 2008) (edit) (undo) Tek (Talk | contribs) m
(2 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	If we determine the number's magnitude <math>r</math> and argument <math>\alpha </math>, we can write its polar form using the formula
-	<center> [[Image:3_2_6b.gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+
		+	{{Displayed math||<math>r(\cos\alpha + i\sin\alpha)\,\textrm{.}</math>}}
		+
		+	Because the number lies on the imaginary axis, it is possible to write its magnitude and argument directly.
	[[Image:3_2_6_b.gif|center]]		[[Image:3_2_6_b.gif|center]]
		+
		+	The polar form is
		+
		+	{{Displayed math||<math>11\Bigl(\cos\frac{3\pi}{2} + i\sin\frac{3\pi}{2}\Bigr)\,\textrm{.}</math>}}

---

Current revision

If we determine the number's magnitude \displaystyle r and argument \displaystyle \alpha , we can write its polar form using the formula

\displaystyle r(\cos\alpha + i\sin\alpha)\,\textrm{.}

Because the number lies on the imaginary axis, it is possible to write its magnitude and argument directly.

The polar form is

\displaystyle 11\Bigl(\cos\frac{3\pi}{2} + i\sin\frac{3\pi}{2}\Bigr)\,\textrm{.}