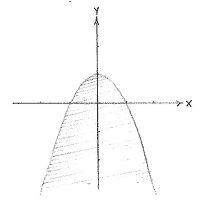
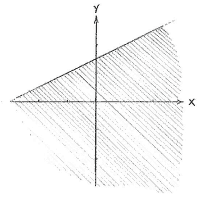
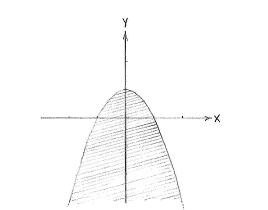
Solution 2.3:10b
From Förberedande kurs i matematik 1
The inequality  1−x2
1−x2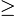 2y−3
2y−3 x
x 2+3
2+3 2
2 2+3
2+3 2
2
| The region y ≤ 1 - x² | The region x ≥ 2y - 3 |
Of the figures above, it seems that the region associated with the parabola lies completely under the line  2+3
2+3 2
2
| The region y ≤ 1 - x² and x ≥ 2y - 3 |
Note: If you feel unsure about whether the parabola really does lie under the line, i.e. that it just happens to look as though it does, we can investigate if the y-values on the line  2+3
2+3 2
2
|
|
If this difference is positive regardless of how x is chosen, then we know that the line's y-value is always greater than the parabola's y-value. After a little simplification and completing the square, we have
 x+41 x+41 2− 2− 41 41 2+21= 2+21= x+41 x+41 2+716 2+716 |
and this expression is always positive because  x+41
x+41 2
2