Processing Math: Done
Solution 3.1:3b
From Förberedande kurs i matematik 1
When simplifying a radical expression, a common technique is to divide up the numbers under the root sign into their smallest possible integer factors and then take out the squares and see if common factors cancel each other out or can be combined together in a new way.
By successively dividing by 2 and 3, we see that
 48=2 48=2 2 2 24=2 24=2 2 2 2 2 12=2 12=2 2 2 2 2 2 2 6=2 6=2 2 2 2 2 2 2 2 2 3=25 3=25 3 3 =2 =2 9=2 9=2 3 3 3=2 3=2 32 32 |
Thus,
 96 96 18= 18=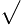 25 25 3= 3=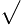 22 22 22 22 2 2 3=2 3=2 2 2  2 2  3 3 = =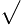 2 2 32=3 32=3  2 2 |
and the whole quotient can be written as
 18 18 96=3 96=3  22 22 2 2  2 2  3=34 3=34 3. 3. |
Note: If it is difficult to work with radicals, it is possible instead to write everything in power form
 18 18 96=181 96=181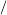 2961 2961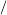 2=(2 2=(2 32)1 32)1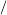 2(25 2(25 3)1 3)1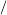 2=221 2=221 32 32 2125 2125 21 21 321=225−21 321=225−21 321−1=22 321−1=22 3−21=4 3−21=4 3=34 3=34 3. 3. |
(In the last equality, we multiply top and bottom by  3
3
