Solution 3.2:1

From Förberedande kurs i matematik 1

In order to get rid of the root sign in the equation, we square both sides

It is important to remember that this step means that we are now working with a new equation which may have solutions which the equation that we started with did not have. At the end, it will therefore be necessary for us to check that the solutions that we calculate satisfy the original equation also.

If we continue with the squared equation and expand the right-hand side, we get a second order equation

i.e.

We complete the square of the left-hand side

x2−13x+40=x−2132−2132+40=x−2132−4169+4160=x−2132−49,

which gives the equation

x−2132=49

which has the solutions

• x=213+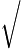49=213+23=216=8 

• x=213−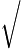49=213−23=210=5. 

Just to be on the safe side, we check whether we have solved the second-order equation (*) correctly by substituting x=5 and x=8 into it:

• x = 5:  LHS=5−4=1  and  RHS=(6−5)2=1

• x = 8:  LHS=8−4=4  and  RHS=(6−8)2=4

Then, we must test the solutions x=5 and x=8 in the original equation:

• x = 5:  LHS=5−4=1   and  RHS=6−5=1

• x = 8:  LHS=8−4=2   and  RHS=6−8=−2

This shows that x=5 is a solution to the original equation, whilst x=8 is a spurious root.

Note: That we get a spurious root does not mean that we calculated incorrectly, but is totally the result of squaring the equation.