Processing Math: Done

From Förberedande kurs i matematik 1

First, we move the 2 to the right-hand side to get 3x−8=x−2  and then square away the root sign,

3x−8=(x−2)2

(*)

or, with the right-hand side expanded

3x−8=x2−4x+4.

If we move over all the terms to the left-hand side, we get

x2−7x+12=0.

If we complete the square of the left-hand side,

x2−7x+12=x−272−272+12=x−272−449+448=x−272−41

the equation can be written as

x−272=41

and the solutions are

• x=27+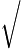41=27+21=28=4 

• x=27−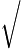41=27−21=26=3. 

To be on the safe side, we verify that x=3 and x=4 satisfy the squared equation (*)

x = 3:	LHS=33−8=9−8=1 and
	RHS=(3−2)2=1
x = 4:	LHS=34−8=12−8=4 and
	RHS=(4−2)2=4

Because we squared the root equation, possible spurious roots turn up and we therefore have to verify the solutions when we go back to the original root equation:

x = 3:	LHS=33−8+2=9−8+2=1+2=3  and
	RHS=3
x = 4:	LHS=34−8−2=12−8+2=2+2=4  and
	RHS=4

The solutions to the root equation are x=3 and x=4.