Processing Math: Done

From Förberedande kurs i matematik 1

After squaring both sides, we obtain the equation

3x−2=(2−x)2

(*)

and if we expand the right-hand side and then collect the terms, we get

x2−7x+6=0.

Completing the square of the left-hand side, we obtain

x2−7x+6=x−272−272+6=x−272−449+424=x−272−425

which means that the equation can be written as

x−272=425

and the solutions are therefore

• x=27+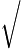425=27+25=212=6 

• x=27−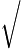425=27−25=22=1. 

Substituting x=1 and x=6 into the quadratic equation (*) shows that we have solved the equation correctly.

• x = 1:  LHS=31−2=1  and  RHS=(2−1)2=1

• x = 6:  LHS=36−2=16  and  RHS=(2−6)2=16

Finally, we need to sort away possible spurious roots to the root equation by verifying the solutions.

• x = 1:  LHS=31−2=1   and  RHS=2−1=1

• x = 6:  LHS=36−2=4   and  RHS=2−6=−4

This shows that the root equation has the solution x=1.