Solution 3.2:6
From Förberedande kurs i matematik 1
This equation differs from earlier examples in that it contains two root terms, in which case it is not possible to get rid of all square roots at once with one squaring, but rather we need to work in two steps.
Squaring once gives
  x+1+ x+1+ x+5 x+5 2=42 2=42 |
and expanding the left-hand side gives
  x+1 x+1 2+2 2+2 x+1 x+1 x+5+ x+5+  x+5 x+5 2=16 2=16 |
which, after simplification, results in the equation
 x+1 x+1 x+5+x+5=16. x+5+x+5=16. |
Moving all the terms, other than the root term, over to the right-hand side,
 x+1 x+1 x+5=−2x+10 x+5=−2x+10 |
and squaring once again,
 2 2 x+1 x+1 x+5 x+5 2=(−2x+10)2 2=(−2x+10)2 |
at last gives an equation that is completely free of root signs,
Expand both sides
and then cancel the common x²-term,
We can write this equation as
 5=522=45. 5=522=45. |
Because we squared our original equation (twice), we have to verify the solution
 4
4
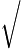 45+1+ 45+1+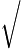 45+5= 45+5=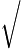 49+ 49+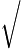 425=23+25=28=4=RHS. 425=23+25=28=4=RHS. |
Thus, the equation has the solution  4
4
