Processing Math: Done

From Förberedande kurs i matematik 1

In the equation, both sides are positive because the factors ex and 3−x are positive regardless of the value of x (a positive base raised to a number always gives a positive number). We can therefore take the natural logarithm of both sides,

ln13ex=ln23−x.

Using the log laws, we can divide up the products into several logarithmic terms,

ln13+lnex=ln2+ln3−x

and using the law lnab=blna, we can get rid of x from the exponents

ln13+xlne=ln2+(−x)ln3.

Collect x on one side and the other terms on the other,

xlne+xln3=ln2−ln13.

Take out x on the left-hand side and use lne=1,

x(1+ln3)=ln2−ln13.

Then, solve for x,

x=1+ln3ln2−ln13.

Note: Because 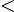ln2ln13, we can write the answer as

x=−1+ln3ln13−ln2

to indicate that x is negative.