Solution 3.4:2b
From Förberedande kurs i matematik 1
If we write the equation as
 ex ex 2+ex=4 2+ex=4 |
we see that
For clarity, we set
and we solve this second-degree equation by completing the square,
 t+21 t+21 2− 2− 21 21 2= 2= t+21 t+21 2−41 2−41 |
which gives
 t+21 t+21 2−41=4 2−41=4 t=−21 t=−21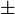 2 2 17. 17. |
These two roots give us two possible values for
 17orex=−21+2 17orex=−21+2 17. 17. |
In the first case, the right-hand side is negative and because "e raised to anything" can never be negative, there is no x that can satisfy this equality. The other case, on the other hand, has a positive right-hand side (because
 17
17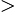 1
1
 2 2 17−21 17−21 . . |
Note: It is a little tricky to check the answer to the original equation, so we can be satisfied with substituting  17
17 2−1
2−1 2
2
 2 2 17−21 17−21 2+ 2+ 2 2 17−21 17−21 =417−2 =417−2 21 21 2 2 17+41+2 17+41+2 17−21=417+41−21=417+1−2=416=4=RHS. 17−21=417+41−21=417+1−2=416=4=RHS. |
