Processing Math: Done
Solution 3.4:3a
From Förberedande kurs i matematik 1
Both left- and right-hand sides are positive for all values of x and this means that we can take the logarithm of both sides and get a more manageable equation,
 ln2 ln2 =ln =ln 2e2x 2e2x =ln2+lne2x=ln2+2x =ln2+lne2x=ln2+2x lne=ln2+2x lne=ln2+2x 1. 1. |
After a little rearranging, the equation becomes
We complete the square of the left-hand side,
 x+1ln2 x+1ln2 2− 2− 1ln2 1ln2 2+1=0 2+1=0 |
and move the constant terms over to the right-hand side,
 x+1ln2 x+1ln2 2= 2= 1ln2 1ln2 2−1. 2−1. |
It can be difficult to see whether the right-hand side is positive or not, but if we remember that 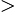 2
2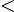 lne=1
lne=1 ln2)2
ln2)2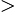 1
1
The equation therefore has the solutions
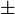 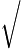  1ln2 1ln2 2−1 2−1 |
which can also be written as
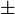 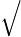 1−(ln2)2. 1−(ln2)2. |
