Solution 3.4:3b
From Förberedande kurs i matematik 1
The expressions  x2+3x
x2+3x
 3x2−2x
3x2−2x
However, we have to be careful! If we obtain a value for x which makes the arguments equal but negative or zero, then it will not correspond to a genuine solution because ln is not defined for negative arguments. At the end of the exercise, we must therefore check that
If we move all the terms over to one side in the equation for the arguments, we get the second-degree equation
and we see that both terms contain x, which we can take out as a factor,
From this factorized expression, we read off that the solutions are  2
2
A final check shows that when  2
2 4
4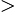 0
0 2
2
