D

Linjär algebra

Versionen från 10 maj 2007 kl. 14.42 (redigera) Annator (Diskussion | bidrag) ← Gå till föregående ändring		Versionen från 10 maj 2007 kl. 15.46 (redigera) (ogör) Annator (Diskussion | bidrag) Gå till nästa ändring →
Rad 1:		Rad 1:
-	Något förenklat kan man säga att den linjära algebran handlar om att översätta geometriska problem till algebraiska och vice versa. Det visar sig att en mycket stor del av de geometriska problem vi kommer att intressera oss för kan översättas till frågor om så kallade linjära ekvationssystem. En linjär ekvation i <math>n</math> obekanta är en ekvation som kan skrivas på formen <math>a_1x_1+a_2x_2+a_3x_3+ \cdots +a_{n-1}x_{n-1}+a_nx_n=0</math> Några exempel på linjära ekvationer i 3 variabler är <math>5x_1+17x_2-12x_3=0</math> och <math>\sqrt(5)x_1-x_2+\pix_3=0</math>. Ekvationen <math>\sqrt{x_1}+x_2-x_3=0</math> är däremot inte linjär. Skriv nu upp två egna exempel på linjära och icke-linjära ekvationer innan du läser vidare.	+	Något förenklat kan man säga att den linjära algebran handlar om att översätta geometriska problem till algebraiska och vice versa. Det visar sig att en mycket stor del av de geometriska problem vi kommer att intressera oss för kan översättas till frågor om så kallade linjära ekvationssystem.
		+
		+	En linjär ekvation i <math>n</math> obekanta är en ekvation som kan skrivas på formen <math>a_1x_1+a_2x_2+a_3x_3+ \cdots +a_{n-1}x_{n-1}+a_nx_n=0</math> Några exempel på linjära ekvationer i 3 variabler är <math>5x_1+17x_2-12x_3=0</math> och <math>\sqrt(5)x_1-x_2+\pix_3=0</math>. Ekvationen <math>\sqrt{x_1}+x_2-x_3=0</math> är däremot inte linjär. Skriv nu upp två egna exempel på linjära och icke-linjära ekvationer innan du läser vidare. Läs sedan igenom sidorna 1-3 (tom exempel 2)i boken. Lös övning 1.1.3 (a) och (c) som en kontroll på att du förstått det du har läst. Välj parametern som beskriver svaret på 1.1.3 (a) på två olika sätt och fundera på vilket samband som finns mellan dina två parametrar.
		+
		+	Ett linjärt ekvationssystem är en uppsättning linjära ekvationer. För att en uppsättning värden <math>(a_1, a_2, \ldots , a_n)</math> skall räknas som en lösning till systemet krävs att alla ekvationer är uppfyllda om man sätter <math>x_1=a_1, x_2=a_2</math> osv. Man kan visa att varje linjärt ekvationssystem har antingen 0, 1 eller oändligt många lösningar.

---

Versionen från 10 maj 2007 kl. 15.46

Något förenklat kan man säga att den linjära algebran handlar om att översätta geometriska problem till algebraiska och vice versa. Det visar sig att en mycket stor del av de geometriska problem vi kommer att intressera oss för kan översättas till frågor om så kallade linjära ekvationssystem.

En linjär ekvation i n obekanta är en ekvation som kan skrivas på formen Några exempel på linjära ekvationer i 3 variabler är 5x₁ + 17x₂ − 12x₃ = 0 och Misslyckades med att tolka formel. (okänt fel): \sqrt(5)x_1-x_2+\pix_3=0 . Ekvationen 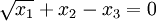är däremot inte linjär. Skriv nu upp två egna exempel på linjära och icke-linjära ekvationer innan du läser vidare. Läs sedan igenom sidorna 1-3 (tom exempel 2)i boken. Lös övning 1.1.3 (a) och (c) som en kontroll på att du förstått det du har läst. Välj parametern som beskriver svaret på 1.1.3 (a) på två olika sätt och fundera på vilket samband som finns mellan dina två parametrar.

Ett linjärt ekvationssystem är en uppsättning linjära ekvationer. För att en uppsättning värden 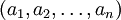skall räknas som en lösning till systemet krävs att alla ekvationer är uppfyllda om man sätter x₁ = a₁,x₂ = a₂ osv. Man kan visa att varje linjärt ekvationssystem har antingen 0, 1 eller oändligt många lösningar.