Lösningar 9

Matematik för naturvetare 15hp

[redigera] Lösningar till några övningar till lektion 9

Tillbaka till lösningarna

14.1.c)

Totalmatrisen är

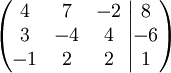
och Gausselimination ger

Lösningen är $x=0, y=1,z=-1/2$

14.2.c)

Totalmatrisen är

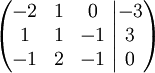
och Gausselimination ger

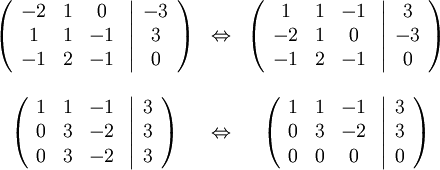
Systemet är alltså ekvivalent med $x+y-z=3, 3y-2z=3$ och det går inte att eliminera längre än så. Inför en parameter $t$ genom t ex $z=3t$. Då blir $y=(3+2z)/3=1+2t$ och $x=-y+z+3=2+t$. Lösningen kan således skrivas $(x,y,z)=(2+t, 1+2t,3t)$. Lägg märke till att man kan införa en parameter (här $t$) på många olika sätt. I bokens facit heter parametern $s$ och det gäller $s=-t$. Anledningen till att vi väljer att sätta $z=3t$ snarare än $z=t$ är att vi får heltalskoefficienter då. Men det är ju helt och hållet en smakfråga om man vill ha det.

14.3.a)

Systemet är ekvivalent med

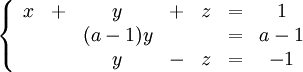
och här måste vi dela upp i två fall beroende på om $a=1$ eller $a\not=1$. Om $a=1$ så lyder den andra ekvationen $0=0$. Om vi sätter $z=t$ så blir $y=-1+t$ och $x=1-y-z=2-2t$, där $t\in{\bf R}$. Om $a\not=1$, så kan vi dividera den andra ekvationen med $a-1$ och får $y=1$. Då blir $z=2$ och $x=-2$.

Svar:

Om $a\not=1$ så är lösningen $(x,y,z)=(-2,1,2)$ och om $a=1$ så är den $(x,y,z)=(2-2t,-1+t,t)$.

14.7.

För att en produkt $AB$ skall vara definierad måste antalet kolonner i $A$ vara lika med antalet rader i $B$. För att $AA$ skall vara definierad måste $A$ därför ha lika många rader som kolonner, dvs den måste vara kvadratisk.

14.10.a)

Som i Exempel 14.12 skall vi försöka lösa de två ekvationssystem som har totalmatriserna

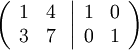
Gausselimination ger

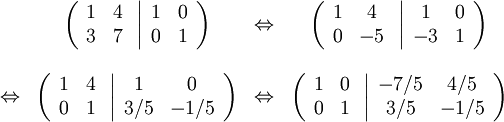
Vi ser att matrisen är inverterbar och att inversen är

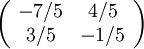
14.10 d)

Gausselimination ger

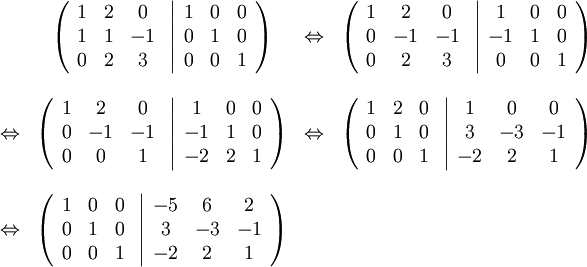
Inversen är alltså