Lektion 5
Matematik för naturvetare 15hp
| Versionen från 5 september 2007 kl. 18.44 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (6 september 2007 kl. 11.04) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) |
||
| Rad 105: | Rad 105: | ||
| - | Begreppet invers funktion är viktigt för att förstå funktioner som potensfunktioner, logaritmer och arcusfunktioner som behandlas i nästa lektion. | + | Begreppet invers funktion är viktigt för att förstå funktioner som potensfunktioner, logaritmer och arcusfunktioner som behandlas i de följande två lektionerna. |
Nuvarande version
[redigera] Välkommen till Lektion 5!
Tillbaka till läsanvisningarna
I den här lektionen behandlar vi det allmänna funktionsbegreppet som är en viktig grund för resten av innehållet i kursen.
Du ska studera följande kapitel i boken:
- 3.1 Funktionsdefinitionen
- 3.2 Monotona funktioner
- 3.3 Inversa funktioner
Viktiga saker att tänka på när du läser
Avsnitt 3.1
Funktionsbegreppet är fundamentalt i matematiken. Viktiga begrepp i
det här kapitlet är definitionsmängd, värdedmängd, sammansatt funktion och invers
funktion. Lär dig beteckningen $f\circ g$ för sammansättningen av $f$
och $g$ som införs mitt på sid 92 och kom ihåg att $(f\circ g)(x)=f(g(x))$. Skilj noga på funktionen $f$ och funktionsvärdet $f(x)$ (som utläses "f av x"). Funktionen är själva regeln som till ett givet $x$ ordnar $f(x)$. Grafen till en funktion $f$ består av alla talpar $(x,y)$ i ett rätvinkligt koordinatsystem som uppfyller att $y=f(x)$. Man kan även rita grafer för samband mellan två variabler $x$ och $y$ som inte är ett funktionssamband, t.ex. $x^2+y^2=1$, se sid 94. Grafen består av alla punkter $(x,y)$ som uppfyller smbandet. Grafen till sambandet $x^2+y^2=1$ är en cirkel med radien 1 och med medelpunkt i origo. Att denna graf inte är grafen till en funktion $y=f(x)$ inser man genom att skära grafen med lodräta linjer. Det får vara högst en skärningspunkt om det är en funktionsgraf, men här är det ibland två skärningspunkter.
Innebörden i beteckningen $f:A\to B$ som införs i boken längst ned på sid 90 skiljer sig från normal standard. Man brukar bara kräva att $A=D_f$ och $V_f\subseteq B$ (dvs inte nödvändigtvis $B=V_f$). T.ex. brukar man skriva att ${\rm sq}: \mathbf R\to \mathbf R$ där ${\rm sq}(x)=x^2$ fastän $V_{sq}=\{x\in\mathbf R|\ x\ge0\}$. Andra exempel är att man brukar skriva $\sin:\mathbf R\to \mathbf R$, där $\sin$ betecknar sinusfunktionen (se lektion 7) och ${\rm exp}:\mathbf R\to \mathbf R$ där ${\rm exp}(x)=e^x$ (se lektion 6), fastän $V_{sin}=[-1,1]$ och $V_{exp}=\mathbf R_+$. Däremot får man inte skriva $\ln:\mathbf R\to\mathbf R$, där $\ln$ betecknar den naturliga logaritmfunktionen (se lektion 6), eftersom $D_{ln}=\mathbf R_+$. Rätt skrivsätt är alltså $\ln:\mathbf R_+\to\mathbf R$ och här gäller det t.o.m. att $V_{\ln}=\mathbf R$, så i det här fallet överensstämmer skrivsättet med bokens.
Sammansättningen av två funktioner kan man betrakta som en räkneregel för fuktioner, i analogi med räkneregler för tal som t.ex. multiplikation. Man måste dock komma ihåg att sammansättningen av två funktioner inte alltid är definierad (men det är ju t.ex. inte division för heltal heller). Om $f:A\to B$ och $g:B\to C$ så är $g\circ f$ definierad (observera ordningen). Funktionen $g\circ f$ är definierad som den funktion som till ett givet $x\in D_f$ först utför funktionen $f$ så att man får elementet $f(x)\in B$ och sedan utför funktionen $g$ på detta element så att man till slut får funktionsvärdet $g(f(x))\in C$. Observera att det räcker att $V_f\subseteq B$ för att $g(f(x))$ skall vara definierat, eftersom $D_g=B$. Rita gärna en figur med tre bollar analog med figuren mitt på sid 90, där $f$ går mellan de två första bollarna och $g$ går från den andra till den tredje bollen.
Exempel 3.7 ger ett exempel på en sammansatt funktion. För att reda ut begreppen, så är det en fördel att vara lite noggrannare än boken. Uttrycket $y=x^2-1$ definierar en funktion $g:\mathbf R\to\mathbf R$ med $D_g=\mathbf R$ och $V_g=[-1,\infty[$ (se figuren överst till höger på sid 92). Vidare studeras $f: \{x\in\mathbf R|\ x\ge0\}\to \mathbf R$ (se figuren överst till vänster på sid 92). Med dessa definitioner så gäller inte att $f\circ g$ är definierad, eftersom t.ex. $f(g(0))=f(-1)$ inte är definierat. Det man kan göra är att inskränka på definitionsmängden för $g$ så att dess värdemängd blir en delmängd av definitionsmängden för $f$. Detta uppnår man genom att ändra på definitionsmängden för $g$ till att vara $\{x\in\mathbf R|\ x\le-1\lor x\ge1\}$ (se figuren till höger igen). På detta sätt erhålles en ny funktion, säg $h$, med $V_h=\{x\in\mathbf R|\ x\ge0\}$ och nu gäller det att $f\circ h$ är definierat och vi har att $f(h(x))=\sqrt{x^2-1}$ för alla $x\in D_h$. Det gäller alltså att skilja på de två funktionerna $g$ och $h$ som gör samma sak med $x$ (kvadrerar och minskar med 1), men är definierade på olika mängder ($g$ för alla reella tal och $h$ endast för de $x$ som uppfyller att $|x|\ge1$).
Sammansättningen i den andra ordningen $g\circ f$ är däremot definierad, eftersom $g(x)$ är definierat för alla $x$. Det gäller att $(g\circ f)(x)=g(f(x))=x-1$ för alla $x\in D_f=\{x\in\mathbf R|\ x\ge0\}$. Definitionsmängden för $g\circ f$ är alltså inte hela $\mathbf R$, fastän uttrycket $x-1$ är definierat för alla $x\in\mathbf R$. Även $h\circ f$ är definierad med samma definitionsmängd som $g\circ f$. Dessutom gäller att $(h\circ f)(x)=(g\circ f)(x)=x-1$ för alla $x$ i definitionsmängden $\{x\in\mathbf R|\ x\ge0\}$. Därför gäller att funktionerna $g\circ f$ och $h\circ f$ är lika, ty två funktioner är lika om de har samma definitionsmängd och samma värde för alla $x$ i definitionsmängden.
I övning 3.7 d) frågas vad sammansättningen $f\circ g\circ g$ är. Man kan fråga sig om man menar $f\circ (g\circ g)$ eller $(f\circ g)\circ g$. Lyckligtvis spelar det ingen roll, dessa två funktioner är lika. Det gäller generellt att $f\circ (g\circ h)=(f\circ g)\circ h$, vilket kallas för den associativa lagen (jämför med motsvarande lag för multiplikation av tal. $a(bc)=(ab)c$), ty båda funktionerna har definitionsmängd $D_h$ och värdet för båda funktionerna i punkten $x$ är $f(g(h(x)))$.
Avsnitt 3.3
Strax efter formel (1) i boken står det
"Men om vi bestämmer att $x\ge 0$ finner vi att ett y-värde alltid motsvarar endast ett x-värde."
Man bör ändra detta till: "... finner vi att ett värde $y\ge1$ alltid motsvarar ..."
Observera innehållet i varningsrutan! Talet $5^{-1}$ är invers till 5 med avseende på multiplikation med innebörden att $5^{-1}*5=1$. För funktioner gäller att $f^{-1}$ är invers till $f$ med avseende på sammansättning, dvs det gäller att $f^{-1}\circ f=id_{D_f}$. Här betyder $id_{D_f}$ den funktion som uppfyller att $id_{D_f}(x)=x$ för alla $x\in D_f$. Se figur längst ned på sid 100. Den formel med två likheter som står ovanför figuren på sid 100 är dock fel. Texten
"För den sammansatta ... gäller följande: $f(f^{-1}(x))=f^{-1}(f(x))=x$"
skall ändras till:
För de sammansatta funktionerna $f\circ f^{-1}$ och $f^{-1}\circ f$ gäller följande:
$$f(f^{-1}(x))=x, \quad x\in V_f$$
$$f^{-1}(f(x))=x, \quad x\in D_f$$
Det är lätt att se i figuren på sid 100 att funktionerna $f\circ f^{-1}$ och $f^{-1}\circ f$ är olika. Den första startar i det högra området ($V_f$) och slutar i samma område, medan den andra funktionen startar och slutar i området till vänster ($D_f$). I exempel 3.15 ser man också att de två likheterna inte gäller för samma $x$. Den första, $f(f^{-1}(x))=x$ gäller för alla $x\ne0$ och den andra, $f^{-1}(f(x))=x$ gäller för alla $x\ne1$.
I beviset av Sats 3.1 står det
"Då $f$ är strängt monoton kan vi också för varje $y$ endast finna ett x-värde."
Detta bör ändras till:
"Då $f$ är strängt monoton kan vi också för varje $y$ finna högst ett x-värde."
Om nämligen $y$ inte tillhör värdemängden för $f$, så finns det inget $x$ så att $f(x)=y$. Exempelvis är funktionen $y=x^2$ med definitionsmängd $\{x\in\mathbf R|\ x\ge0\}$ strängt monoton och har en invers (som är $y=\sqrt x$). Här gäller att ekvationen $y=x^2$ saknar lösningar om $y<0$. Om däremot $y\ge0$ så finns precis ett $x$ i definitionsmängden som uppfyller att $y=x^2$.
Det är viktigt att du inser
sambandet mellan graferna till funktionerna $y=f(x)$ och
$y=f^{-1}(x)$, nämligen att de är varandras spegelbilder i linjen $y=x$.
I boken finns en kortfattad förklaring till detta och här följer
ytterligare en förklaring.
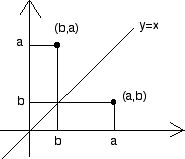
Lägg först märke till att punkterna $(a,b)$ och $(b,a)$ är varandras spegelbilder i linjen $y=x$.
Vi har för det andra
$$ (a,b)\text{ ligger på grafen till } y=f(x) \Leftrightarrow b=f(a) \Leftrightarrow a=f^{-1}(b) \Leftrightarrow (b,a)\text{ ligger på grafen till } y=f^{-1}(x)$$
vilket visar påståendet.
Begreppet invers funktion är viktigt för att förstå funktioner som potensfunktioner, logaritmer och arcusfunktioner som behandlas i de följande två lektionerna.
Lämpliga övningsuppgifter till Lektion 5
Välj bland följande uppgifter i boken: 3.1-3.5, 3.7-3.11.