Lektion 8

Matematik för naturvetare 15hp

(Skillnad mellan versioner)

Nuvarande version

[redigera] Välkommen till Lektion 8!

I den här lektionen ska vi lära oss vad komplexa tal är för något och hur man räknar med dem och olika sätt att representera dem.

Du ska studera följande kapitel i boken:

1.9 De komplexa talen
13.7 Lite mer om komplexa tal

Viktiga saker att tänka på när du läser

Avsnitt 1.9

Lägg märke till att om $z=a+ib$, så är det talet $b$ som är imaginärdelen, alltså inte $ib$. Både real- och imaginärdelarna av $z$ är reella tal. Observera också att absolutbeloppet är $|z|=\sqrt{a^2+b^2}$, inte $\sqrt{a^2+(ib)^2}$. Om $b=0$ så är $z=a$ ett reellt tal med absolutbelopp $|z|=\sqrt{a^2}=|a|$, där det sista ledet är det vanliga reella absolutbeloppet. För reella tal överensstämmer således det komplexa absolutbeloppet med det reella.

Med hjälp av Pythagoras sats så ser vi att $|a+ib|=\sqrt{a^2+b^2}$ är avståndet från origo till punkten $a+ib$ (se längst ned på sid 49).

Addition, subtraktion och multiplikation av komplexa tal går till så att man "räknar som vanligt" men kommer ihåg att $i^2=-1$. Det betyder t.ex. att produkten av $a+ib$ och $c+id$ är

$$(a+ib)(c+id)=(ac-bd)+i(ad+bc)$$

Tillämpar man detta på produkten $z\cdot \overline z$ där $z=a+ib$ så får man $z\cdot \overline z=(a+ib)(a-ib)=a^2+b^2=|z|^2$ (se också här längst ned på sid 49).

I Exempel 1.31 drar man kvadratroten ur ett negativt tal $\sqrt{-16}=±4i$. Normalt brukar man dock reservera beteckningen $\sqrt a$ för reella tal $a\ge 0$, annars är det lätt hänt att beteckningarna leder en vilse:

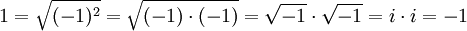
$1=\sqrt{(-1)^2}=\sqrt{(-1)\cdot (-1)}=\sqrt{-1}\cdot\sqrt{-1}=i\cdot i=-1$

Var är felet?

Konjugering och absolutbelopp har vissa viktiga egenskaper som man ofta har användning av, men som inte diskuteras i avsnittet (se dock övning 1.47). Vi skall göra det här istället. Låt $z=a+ib$ vara ett komplext tal; dess konjugat är $\overline{z}=a-ib$, så

$$ z\cdot\overline{z}=(a+ib)(a-ib)=a^2-(ib^2)=a^2+b^2=|z|^2$$

Låt $w=c+id$ vara ett annat komplext tal. Då är

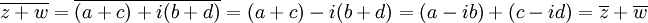
$\overline{z+w}=\overline{(a+c)+i(b+d)}=(a+c)-i(b+d)=(a-ib)+(c-id)= \overline{z}+\overline{w}$

dvs konjugatet av en summa är lika med summan av konjugaten (se övning 1.47 a).

Motsvarande gäller för produkter:

$$ zw=(a+ib)(c+id)=ac-bd+i(ad+bc),\quad\mbox{så att}\quad \overline{zw}=ac-bd-i(ad+bc)$$

Vidare är

$$ \overline{z}\cdot\overline{w}=(a-ib)(c-id)=ac-bd-i(ad+bc)$$

Alltså gäller (övning 1.47 b)

$$ \overline{zw}=\overline{z}\cdot\overline{w}$$

Av detta följer vidare

$$ |zw|^2=(zw)\cdot \overline{zw}=z\cdot w\cdot\overline{z}\cdot \overline{w}= (z\cdot\overline{z})\cdot (w\cdot\overline{w})=|z|^2\cdot |w|^2=(|z|\cdot |w|)^2$$

och drar vi kvadratroten ur båda ytterleden så får vi

$$ |zw|=|z|\cdot |w|$$

Däremot skall man komma ihåg att $|z+w|$ i allmänhet inte är lika med $|z|+|w|$, utan bara att det gäller

$$ |z+w|\le |z|+|w|$$

vilket kallas triangelolikheten eftersom det kan tolkas som att längden av en sida i en triangel altid är mindre än summan av de övriga två. Beviset hoppar vi över.

Avsnitt 13.7

I detta avsnitt får man lära sig att skriva ett komplext tal $z$ på "polär form", dvs man anger avståndet från $z$ till origo, $|z|$, och vilken vinkel, "argumentet", som linjen från origo till $z$ bildar med positiva reella axeln. Se också sid 121 för definition av denna vinkel. Flera olika vinklar beskriver samma läge för $z$. Man kan t.ex. använda vinklarna $90^\circ, -270^\circ, 450^\circ$ för att ge argumentet för ett komplext tal på den positiva imaginära axeln. Argumentet för $z$, som skrives $\arg z$ är alltså inte entydigt bestämt. Man kan alltid lägga till eller dra bort ett helt antal varv (dvs en multipel av $360^\circ$, eller $2\pi$ radianer). Som det står nederst på sid 353, så brukar man vanligen bestämma sig för att ange argumentet i intervallet

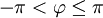
$-\pi<\varphi\le\pi$

(observera att man skall ha sträng olikhet till vänster för att få entydighet).

Som det står ovanför bilden på sid 352, så är de polära koordinaterna för $z$ lika med $(|z|,\arg z)$. I rutan längst ned på samma sida står ett annat mer vanligt sätt att skriva den polära formen. Man måste dock komma ihåg att $\cos\varphi$ och $\sin\varphi$ inte får räknas ut. Talet $1+i$ har den polära formen som står på sid 353:

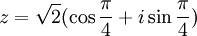
$z=\sqrt2(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4})$

Skulle man stoppa in värdena på $\cos\frac{\pi}{4}=1/\sqrt2$ och $\sin\frac{\pi}{4}=1/\sqrt2$ så skulle man få $z=1+i$ vilket ju är den vanliga formen med rätvinkliga koordinater och inte den polära formen.

Av Sats 13.2 följer en viktig princip för hur multiplikation av två komplexa tal kan beskrivas om man har talen givna på polär form:

$$ (r_1e^{i\varphi_1})\cdot(r_2e^{i\varphi_2})=r_1r_2e^{i(\varphi_1+\varphi_2)} $$

dvs

"absolutbeloppen multipliceras och argumenten adderas vid multiplikation av två komplexa tal".

Av Sats 13.3 följer motsvarande princip för division av två komplexa tal, dvs

"absolutbeloppen divideras och argumenten subtraheras vid division av två komplexa tal".

I slutet av Exempel 13.29 kan man lägga till "dvs $C_2=\overline{C_1}$".

Lämpliga övningsuppgifter till Lektion 8

Välj bland följande uppgifter i boken: 1.44 - 1.47, 13.21 - 13.23

Tillbaka till läsanvisningarna

Den här artikeln är hämtad från http://wiki.math.se/wikis/mm1001_0701/index.php/Lektion_8

Lektion 8

Matematik för naturvetare 15hp

Nuvarande version

[redigera] Välkommen till Lektion 8!

Visningar

Personliga verktyg

Navigering

Sök

Verktygslåda

 vilket kallas ''triangelolikheten'' eftersom det kan tolkas som att längden av en sida i en triangel altid är mindre än summan av de övriga två. Beviset hoppar vi över.
 '''Avsnitt 13.7'''
+I detta avsnitt får man lära sig att skriva ett komplext tal $z$ på "polär form", dvs man anger avståndet från $z$ till origo, $|z|$, och vilken vinkel, "argumentet", som linjen från origo till $z$ bildar med positiva reella axeln. Se också sid 121 för definition av denna vinkel. Flera olika vinklar beskriver samma läge för $z$. Man kan t.ex. använda vinklarna $90^\circ, -270^\circ, 450^\circ$ för att ge argumentet för ett komplext tal på den positiva  imaginära axeln. Argumentet för $z$, som skrives $\arg z$ är alltså inte entydigt bestämt. Man kan alltid lägga till eller dra bort ett helt antal varv (dvs en multipel av $360^\circ$, eller $2\pi$ radianer). Som det står nederst på sid 353, så brukar man vanligen bestämma sig för att ange argumentet i intervallet
+<math>-\pi<\varphi\le\pi</math>
+(observera att man skall ha sträng olikhet till vänster för att få entydighet).
+Som det står ovanför bilden på sid 352, så är de polära koordinaterna för $z$ lika med $(|z|,\arg z)$. I rutan längst ned på samma sida står ett annat mer vanligt sätt att skriva den polära formen. Man måste dock komma ihåg att $\cos\varphi$ och $\sin\varphi$ inte får räknas ut. Talet $1+i$ har den polära formen som står på sid 353:
+<math>z=\sqrt2(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4})</math>
+Skulle man stoppa in värdena på $\cos\frac{\pi}{4}=1/\sqrt2$ och $\sin\frac{\pi}{4}=1/\sqrt2$ så skulle man få $z=1+i$ vilket ju är den vanliga formen med rätvinkliga koordinater och inte den polära formen.
+Av Sats 13.2 följer en viktig princip för hur multiplikation av två komplexa tal kan beskrivas om man har talen givna på polär form:
+$$
+(r_1e^{i\varphi_1})\cdot(r_2e^{i\varphi_2})=r_1r_2e^{i(\varphi_1+\varphi_2)}
+$$
+dvs
+"absolutbeloppen multipliceras och argumenten adderas vid multiplikation av två komplexa tal".
+Av Sats 13.3 följer motsvarande princip för division av två komplexa tal, dvs
+"absolutbeloppen divideras och argumenten subtraheras vid division av två komplexa tal".
+I slutet av Exempel 13.29 kan man lägga till "dvs $C_2=\overline{C_1}$".