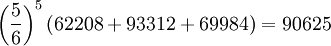Lösningar 10

Matematik för naturvetare 15hp

Versionen från 20 september 2007 kl. 18.31 (redigera) Clas Löfwall (Diskussion | bidrag) (Ny sida: Oftast kan man beräkna en determinant på många olika sätt och det finns inget sätt som är mer "rätt" än något annat, men en del metoder ger mindre arbete än andra. '''14.14 a)...) ← Gå till föregående ändring		Nuvarande version (20 september 2007 kl. 18.32) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag)
Rad 1:		Rad 1:
		+	==Lösningar till några övningar till lektion 10==
		+
		+	[[Exempellösningar|Tillbaka till lösningarna]]
		+
	Oftast kan man beräkna en determinant på många olika sätt och det		Oftast kan man beräkna en determinant på många olika sätt och det
	finns inget sätt som är mer "rätt" än något annat, men en del metoder ger		finns inget sätt som är mer "rätt" än något annat, men en del metoder ger

---

Nuvarande version

[redigera] Lösningar till några övningar till lektion 10

Tillbaka till lösningarna

Oftast kan man beräkna en determinant på många olika sätt och det finns inget sätt som är mer "rätt" än något annat, men en del metoder ger mindre arbete än andra.

14.14 a)

Definitionen av $2\times 2$-determinat ger direkt $$ \left|\begin{array}{cc} 1 & 4\\ 3 & 7\end{array}\right|=1\cdot 7-4\cdot 3=-5$$

14.14 c)

Enligt egenskap 3 hos determinanter ändras inte värdet om vi adderar rad 2 och 3 till rad 1, så $$ \left|\begin{array}{ccc} 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 1\end{array}\right|= \left|\begin{array}{ccc} 5 & 5 & 5 \\ 2 & 1 & 2 \\ 2 & 2 & 1\end{array}\right|= 5\left|\begin{array}{ccc} 1 & 1 & 1 \\ 2 & 1 & 2 \\ 2 & 2 & 1\end{array}\right|$$

där den andra likheten följer av egenskap 2. Subtrahera 2 gånger rad 1 från rad 2 och rad 3:

$$ 5\left|\begin{array}{ccc} 1 & 1 & 1 \\ 2 & 1 & 2 \\ 2 & 2 & 1\end{array}\right|= 5\left|\begin{array}{ccc} 1 & 1 & 1 \\ 0 & -1 & 0 \\ 0 & 0 & -1\end{array}\right|$$

Addera rad 2 och 3 till rad 1:

$$ 5\left|\begin{array}{ccc} 1 & 1 & 1 \\ 0 & -1 & 0 \\ 0 & 0 & -1\end{array}\right|= 5\left|\begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1\end{array}\right|=5$$

14.14 e)

Subtrahera rad 4 från rad 2 och 3 och 2 gånger rad 4 från rad 1:

$$ \left|\begin{array}{cccc} 2 & 3 & 1 & -1 \\ 1 & 2 & -1 & 1 \\ 1 & 1 & 2 & -1 \\ 1 & 1 & 1 & 2\end{array}\right|= \left|\begin{array}{cccc} 0 & 1 & -1 & -5 \\ 0 & 1 & -2 & -1 \\ 0 & 0 & 1 & -3 \\ 1 & 1 & 1 & 2\end{array}\right|$$

Utveckling längs första kolonnen ger

$$ \left|\begin{array}{cccc} 0 & 1 & -1 & -5 \\ 0 & 1 & -2 & -1 \\ 0 & 0 & 1 & -3 \\ 1 & 1 & 1 & 2\end{array}\right|=-\left|\begin{array}{ccc} 1 & -1 & -5 \\ 1 & -2 & -1 \\ 0 & 1 & -3\end{array}\right|$$

Subtrahera rad 1 från rad 2:

$$ -\left|\begin{array}{ccc} 1 & -1 & -5 \\ 1 & -2 & -1 \\ 0 & 1 & -3\end{array}\right|= -\left|\begin{array}{ccc} 1 & -1 & -5 \\ 0 & -1 & 4 \\ 0 & 1 & -3\end{array}\right|$$

Utveckla längs första kolonnen:

$$ -\left|\begin{array}{ccc} 1 & -1 & -5 \\ 0 & -1 & 4 \\ 0 & 1 & -3\end{array}\right|= -\left|\begin{array}{cc} -1 & 4 \\ 1 & -3\end{array}\right|= -((-1)\cdot (-3)-4\cdot 1)=1$$

Svaret är således $1$.

14.14 f)

Tips: Börja med att addera rad 2, 3 och 4 till rad 1.

14.15 a)

Den karaktäristiska ekvationen, dvs $\det (A-\lambda E)=0$, är

$$ \left|\begin{array}{cc} 1-\lambda & -2 \\ -5 & 4-\lambda\end{array}\right|=0$$

Utveckling av determinanten ger

$$ (1-\lambda)(4-\lambda)-(-2)(-5)=0\quad\mbox{eller}\quad \lambda^2-5\lambda -6=0$$

Lösningarna, dvs egenvärdena till matrisen, är $\lambda_{1}=-1$ och $\lambda_{2}=6$. För att bestämma egenvektorerna måste vi lösa systemen $AX=\lambda X$ för de två egenvärdena.

$\mathbf{\lambda_{1}=-1}$:

Här får vi

$$ \left\{\begin{array}{cccccccc} x & - & 2y & = & -x\\ -5x & + & 4y & = & -y\end{array}\right. \quad\mbox{eller}\quad \left\{\begin{array}{cccccccc} 2x & - & 2y & = & 0\\ -5x & + & 5y & = & 0\end{array}\right.$$

Båda ekvationerna är ekvivalenta med $x=y$, så egenvektorerna är $t(1,1)$ för $t\in{\bf R}$, $t\not=0$.

$\mathbf{\lambda_{1}=6}$:

Här får vi

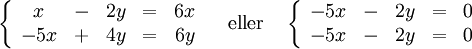
Om vi inför parametern $t$ genom $y=5t$ så blir $x=-2y/5=-2t$. Egenvektorerna är således $t(-2,5)$ för $t\in{\bf R}$, $t\not=0$.

14.15 d)

Den karaktäristiska ekvationen är

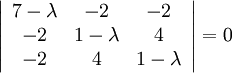
Utveckling av determinanten ger ekvationen

− λ³ + 9λ² + 9λ − 81 = − (λ³ − 9λ² − 9λ + 81) = 0

Här kan man manipulera ekvationen så här:

λ³ − 9λ² − 9λ + 81 = λ²(λ − 9) − 9(λ − 9) = (λ − 9)(λ² − 9) = (λ − 9)(λ + 3)(λ − 3)

Rötterna är tydligen $±3$ och 9 (gissning enligt receptet ovan går förstås bra också).

$\mathbf{\lambda=3}$:

Systemet $AX=\lambda X$ blir

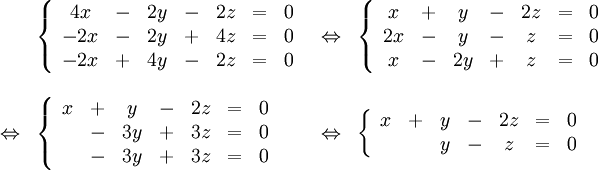
Om man sätter $z=t$ så blir $y=z=t$ och $x=-y+2z=t$. Egenvektorerna är $t(1,1,1)$ för $t\in{\bf R}$, $t\not=0$.

$\mathbf{\lambda=-3}$:

Systemet $AX=\lambda X$ blir

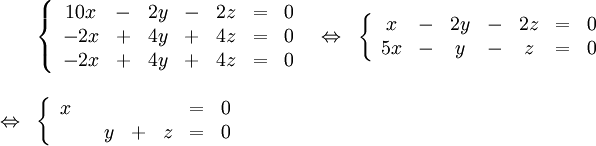
Egenvektorerna är $t(0,1,-1)$ för $t\in{\bf R}$, $t\not=0$.

$\mathbf{\lambda=9}$:

Systemet $AX=\lambda X$ blir

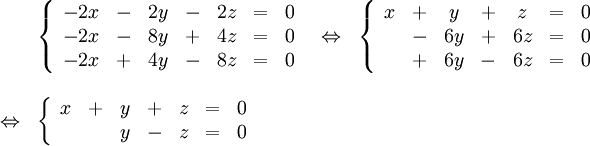
Egenvektorerna är $t(-2 ,1,1)$ för $t\in{\bf R}$, $t\not=0$.

14.15 e)

Den karaktäristiska ekvationen är

Rötterna måste gå jämnt upp i 5, så de enda möjligheterna är $±1$ och $±5$. Prövning ger att de är 1 och 5 (det finns alltså bara 2 olika rötter).

$\mathbf{\lambda =1}$:

Systemet $AX=\lambda X$ blir

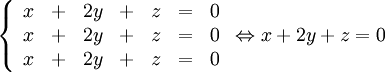
Här måste vi införa två parametrar, t ex genom $y=s,z=t$. Då blir $x=-2y-z=-2s-t$, så att egenvektorerna kan skrivas $(-2s-t,s,t)=s(-2,1,0)+t(-1,0,1)$ för $s,t\in{\bf R}$, $s,t$ ej båda 0.

$\mathbf{\lambda =5}$:

Systemet $AX=\lambda X$ blir

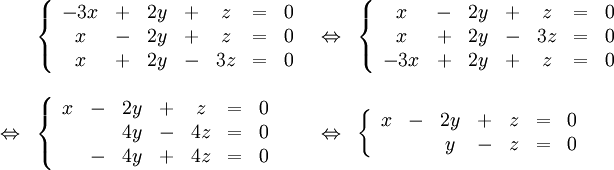
Egenvektorerna är $t(1,1,1)$ för $t\in{\bf R}$, $t\not=0$.

14.15 f)

Den karaktäristiska ekvationen är

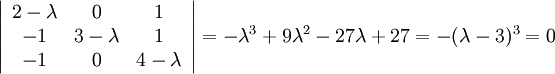
Här finns det tydligen bara en rot, så det enda egenvärdet är $\lambda =3$ (om man inte omedelbart ser att ekvationen kan skrivas $-(\lambda-3)^3=0$ så kan man förstås gissa rötter som ovan). Systemet $AX=\lambda X$ blir

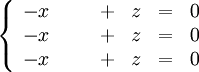
Här kan vi införa parametrar genom t ex $y=s,z=t$ och egenvektorerna blir $(t,s,t)=s(0,1,0)+t(1,0,1)$, där inte både $s$ och $t$ är 0.

14.16.

Den karaktäristiska ekvationen är

Alltså är $a-\lambda=±b$ och egenvärdena är $\lambda=a±b$. Om $b=0$ så finns det alltså bara ett egenvärde. Systemet $AX=\lambda X$ blir bara $ax=ax$ och $ay=ay$, dvs alla $X\not=0$ är egenvektorer. Man kan skriva dem $s(1,0)+t(0,1)$ om man vill. Antag nu att $b\not=0$.

$\mathbf{\lambda=a-b}$:

Systemet $AX=\lambda X$ blir

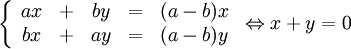
Egenvektorerna är $t(1,-1)$.

$\mathbf{\lambda=a+b}$:

Systemet $AX=\lambda X$ blir

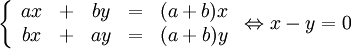
Egenvektorerna är $t(1,1)$.

14.17.b)

Enligt definitionen av karaktäristiskt polynom är

(Lägg märke till att $ad-bc$ är $\det A$. Talet $a+d$ kallas spåret av $A$.) Alltså är

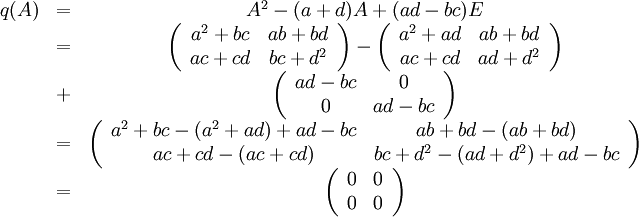
14.21.b)

Direkt uträkning ger

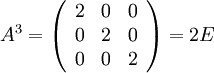
så att $A^3X=2X$ för alla $X$. Det här innebär att populationen fördubblas efter 3 år.

14.21.c)

Antag att $X_{0}$ vore ett sådant startvärde, dvs $AX_{0}=X_{0}$. Detta ger $A^3X_{0}=X_{0}$, men enligt b) har vi $A^3X_{0}=2X_{0}$. Detta är en motsägelse, så svaret är nej.

14.22.

Låt den stabila populationen vara $X_{0}$, så att $AX_{0}=X_{0}$. Om

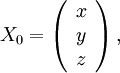
så blir systemet $AX_{0}=X_{0}$

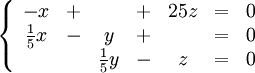
Alltså är $X_{0}=t(25,5,1)$ för $t\in{\bf R}$, $t\not=0$. Proportionerna är således $25:5:1$.

14.23.

Enligt övning 14.16 är egenvärdena $0,6±0,4$, dvs 1 och $0,2$. Motsvarande egenvektorer är $t(1,1)$ och $t(1,-1)$. Startvärdet som gör systemet stabilt är $X_{0}=t(1,1)$ och förhållandet mellan sjuka och friska är $1:1$.

14.25.a)

Låt $b(t)$, $f(t)$ och $p(t)$ beteckna antalet barn, förvärvsarbetande respektive pensionärer efter $t$ tioårsperioder. Enligt texten är

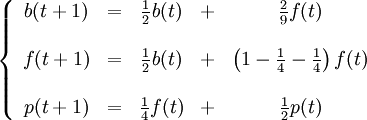
så att övergångsmatrisen är

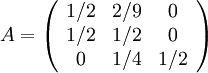
14.25.b)

Vi har $b(0)=62208$, $f(0)=93312$ och $p(0)=69984$. Sätter man

så kontrollerar man omedelbart att

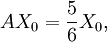
dvs att $X_{0}$ är en egenvektor till $A$ med egenvärde $5/6$. Alltså är

vilket ger att den totala befolkningen efter 50 år är