Lösningar 11
Matematik för naturvetare 15hp
| Versionen från 2 oktober 2007 kl. 09.35 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 2 oktober 2007 kl. 09.36 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 14: | Rad 14: | ||
| Börja med att förlänga med $x-1$: | Börja med att förlänga med $x-1$: | ||
| - | $$ | + | <math> |
| - | \begin{array} | + | \begin{array}{ccccc} |
| \lim_{x\to -1}\frac{\sin(x^2-1)}{x+1}&=& | \lim_{x\to -1}\frac{\sin(x^2-1)}{x+1}&=& | ||
| - | \lim_{x\to -1}(x-1)\frac{\sin(x^2-1)}{x^2-1}= | + | \lim_{x\to -1}(x-1)\frac{\sin(x^2-1)}{x^2-1}&=& |
| \lim_{x\to -1}(x-1)\lim_{x\to -1}\frac{\sin(x^2-1)}{x^2-1}\\ | \lim_{x\to -1}(x-1)\lim_{x\to -1}\frac{\sin(x^2-1)}{x^2-1}\\ | ||
| &=& | &=& | ||
| - | -2\lim_{x\to -1}\frac{\sin(x^2-1)}{x^2-1}\end{array}$$ | + | -2\lim_{x\to -1}\frac{\sin(x^2-1)}{x^2-1}\end{array}&&</math> |
| Sätt $t=x^2-1$; då gäller $t\to 0$ då $x\to -1$. Alltså är | Sätt $t=x^2-1$; då gäller $t\to 0$ då $x\to -1$. Alltså är | ||
Versionen från 2 oktober 2007 kl. 09.36
Lösningar till några övningar till lektion 11
5.1.
Här är det bara att sätta in de olika värdena på $x$ eftersom inga nämnare blir 0.
5.2. a)
Börja med att förlänga med $x-1$:
Misslyckades med att tolka formel. (okänt fel): \begin{array}{ccccc} \lim_{x\to -1}\frac{\sin(x^2-1)}{x+1}&=& \lim_{x\to -1}(x-1)\frac{\sin(x^2-1)}{x^2-1}&=& \lim_{x\to -1}(x-1)\lim_{x\to -1}\frac{\sin(x^2-1)}{x^2-1}\\ &=& -2\lim_{x\to -1}\frac{\sin(x^2-1)}{x^2-1}\end{array}&&
Sätt $t=x^2-1$; då gäller $t\to 0$ då $x\to -1$. Alltså är
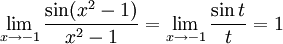
Det sökta gränsvärdet är således $-2$.
5.2. b)
Sätt $x=0$.
5.2. c)
Eftersom $x^2-9=(x-3)(x+3)$ så är
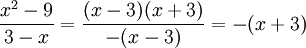
för $x\not=3$. Alltså är
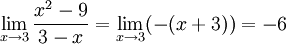
d) Både täljare och nämnare är 0 för $x=-2$ och enligt faktorsatsen är de delbara med $x-(-2)=x+2$. Division ger $x^2+x-2=(x+2)(x-1)$ och $x^2-4=(x+2)(x-2)$. Alltså är \[ \lim_{x\to -2}\frac{x^2+x-2}{x^2-4}=\lim_{x\to -2}\frac{(x+2)(x-1)}{(x+2)(x-2)}= \lim_{x\to -2}\frac{x-1}{x-2}=\frac{-2-1}{-2-2}=\frac{3}{4}.\]
\vskip 2mm
e) Här är knepet att förlänga med $\sqrt{1-x^2}+\sqrt{1+x^2}$:\begin{eqnarray*} \lim_{x\to 0}\frac{\sqrt{1-x^2}-\sqrt{1+x^2}}{x^2}&=& \lim_{x\to 0}\frac{(\sqrt{1-x^2}+\sqrt{1+x^2})(\sqrt{1-x^2}-\sqrt{1+x^2})} {(\sqrt{1-x^2}+\sqrt{1+x^2})x^2}\\ &=& \lim_{x\to 0}\frac{(1-x^2)-(1+x^2)}{(\sqrt{1-x^2}+\sqrt{1+x^2})x^2}\\ &=& \lim_{x\to 0}\frac{-2x^2}{(\sqrt{1-x^2}+\sqrt{1+x^2})x^2}\\ &=& \lim_{x\to 0}\frac{-2}{\sqrt{1-x^2}+\sqrt{1+x^2}}=\frac{-2}{1+1}=-1.\end{eqnarray*}
\vskip 2mm
f) Förläng med $\sqrt x+1$:\begin{eqnarray*} \lim_{x\to 1}\frac{\sqrt x-1}{1-x}&=& \lim_{x\to 1}\frac{(\sqrt x+1)(\sqrt x-1)}{(\sqrt x+1)(1-x)}= \lim_{x\to 1}\frac{x-1}{(\sqrt x+1)(1-x)}\\ &=& \lim_{x\to 1}\left(-\frac{1}{\sqrt x+1}\right)=-\frac{1}{2}.\end{eqnarray*}
\vskip 2mm
5.3.a) Eftersom $|\sin x^2|\le 1$ så är gränsvärdet 0.
\vskip 2mm
b) Skriv $\ln x^2=2\ln x$ och använd ett standardgränsvärde.
\vskip 2mm
c) Standardgränsvärde.
\vskip 2mm
d) Sätt $x=-t$. Då har vi $t\to\infty$ då $x\to-\infty$, så gränsvärdet är \[ \lim_{x\to-\infty}x^3e^x=\lim_{t\to\infty}(-t)^3e^{-t}= -\lim_{t\to\infty}t^3e^{-t}=0\] enligt ett standardgränsvärde.
\vskip 2mm
e) Förkorta med $x^2$: \[ \lim_{x\to\infty}\frac{x^2-3x}{3-2x^2}= \lim_{x\to\infty}\frac{1-3/x}{3/x^2-2}=\frac{1}{-2}=-\frac{1}{2}.\]
\vskip 2mm
f) Förkorta med $x^3$.
\vskip 2mm
5.4.a) Här kan man t ex sätta $t=x-1$, så att $t\to 0$ då $x\to 1$. Vi har $x^3-x=(t+1)^3-(t+1)=t^3+3t^2+2t=t(t^2+3t+2)$, så \begin{eqnarray*} \lim_{x\to 1}\frac{\sin(x-1)}{x^3-x}&=& \lim_{t\to 0}\frac{\sin t}{t(t^2+3t+2)}\\ &=& \lim_{t\to 0}\frac{\sin t}{t}\cdot \lim_{t\to 0}\frac{1}{t^2+3t+2}= 1\cdot\frac{1}{0+0+2}=\frac{1}{2}.\end{eqnarray*}
\vskip 2mm
b) \[ \lim_{x\to 0}\frac{\tan(x-¹)}{x}= \lim_{x\to 0}\frac{\sin(x-¹)}{x\cos(x-¹)}= \lim_{x\to 0}\frac{-\sin x}{-x\cos x}= \lim_{x\to 0}\frac{\sin x}{x}\cdot\lim_{x\to 0}\frac{1}{\cos x}=1\]
\vskip 2mm
c) Nämnaren, men inte täljaren, är 0 för $x=2$, så gränsvärdet existerar inte.
\vskip 2mm
d) Sätt in $x=-1$.
\vskip 2mm
e) Här måste man förlänga med både $\sqrt{x+1}+1$ och $\sqrt{1-x}+1$. Lite räknande ger \begin{eqnarray*} \frac{\sqrt{x+1}-1}{\sqrt{1-x}-1}&=& \frac{(\sqrt{x+1}-1)(\sqrt{x+1}+1)(\sqrt{1-x}+1)} {(\sqrt{1-x}-1)(\sqrt{1-x}+1)(\sqrt{x+1}+1)}\\ &=& \frac{x(\sqrt{1-x}+1)}{(-x)(\sqrt{x+1}+1)}\\ &=& -\frac{\sqrt{1-x}+1}{\sqrt{x+1}+1}\end{eqnarray*} Gränsvärdet då $x\to 0$ är således $-2/2=-1$.
\vskip 2mm
f) Förkorta med $x^3$ och använd att $x^{-1}\ln x\to 0$ då $x\to\infty$.
\vskip 2mm
5.5.a) Vi har $\arctan t\to±¹/2$ då $t\to±\infty$ och $\arctan 0=0$, så gränsvärdet är $(¹/2-0)/(-¹/2)=-1$.
\vskip 2mm
b) Skriv t ex \[ \frac{x\ln x}{2^x}=\frac{x^{-1}\ln x}{2^x/x^2}.\] Här går täljaren mot 0 och nämnaren mot $\infty$ då $x\to\infty$, så gränsvärdet är 0.
\vskip 2mm
c) Förkortar man med $x^3e^{x}$ så får man \[ \frac{1+x^{-3}e^{-x}}{x^{-1}e^x-2x^{-2}e^{-2x}}.\] Nu gäller att $x^{-3}e^{-x}$ och $2x^{-2}e^{-2x}$ går mot 0 samt att $x^{-1}e^x$ går mot $\infty$ då $x\to\infty$, så gränsvärdet är 0.
\vskip 2mm
d) \[ \lim_{x\to 0}\frac{\sin 4x}{\sin x}=4\lim_{x\to 0}\frac{\sin 4x}{4x}\cdot\frac{x}{\sin x}= 4\lim_{x\to 0}\frac{\sin 4x}{4x}\cdot\lim_{x\to 0}\frac{x}{\sin x}=4\cdot 1\cdot 1=4\]
\vskip 2mm
e) Förläng med $1+\cos x$: \[ \frac{1-\cos x}{x^2}=\frac{1-\cos^2x}{x^2(1+\cos x)}= \frac{\sin^2x}{x^2(1+\cos x)}= \left(\frac{\sin x}{x}\right)^2\frac{1}{1+\cos x}\] Detta går mot $1^2\cdot (1/2)=1/2$ då $x\to 0$. Observera att det här betyder att $1-\cos x\approx x^2/2$ eller $\cos x\approx 1-x^2/2$ då $x$ är nära 0.
\vskip 2mm
f) Jämför med e).
\vskip 2mm
5.6.a) \[ \lim_{x\to 0}\frac{e^{2x}-1}{x}=2\lim_{x\to 0}\frac{e^{2x}-1}{2x}=2\cdot 1=2\]
\vskip 2mm
b) \[ \lim_{x\to 0}\frac{\ln(1-2x)}{x}=(-2)\lim_{x\to 0}\frac{\ln(1-2x)}{-2x}= (-2)\cdot 1=-2\]
\vskip 2mm
c) Sätt $t=x-1$ så att $t\to 0$ då $x\to 1$. Vi får \[ \lim_{x\to 1}\frac{x-1}{\ln x}=\lim_{t\to 0}\frac{t}{\ln(1+t)}=1.\]
\vskip 2mm
d) \[ \lim_{x\to 0}\arctan \frac{\tan x}{x\cos x}=\lim_{x\to 0}\arctan \frac{\sin x}{x\cos^2x}=\arctan 1=\frac{¹}{4}\]
\vskip 2mm
5.7.a) $\ln 1=0$
\vskip 2mm
b) Förkortning med $x-2$ ger \[ \lim_{x\to 2}\ln\frac{x^2-2x}{2x-4}=\lim_{x\to 2}\ln\frac{x(x-2)}{2(x-2)}= \lim_{x\to 2}\ln\frac{x}{2}=\ln \frac{2}{2}=\ln 1=0.\]
\vskip 2mm
c) \begin{eqnarray*} \lim_{x\to\infty}(\ln(2x^2-x)-\ln(x^2-1))&=& \lim_{x\to\infty}\ln\frac{2x^2-x}{x^2-1}= \lim_{x\to\infty}\ln\frac{2-1/x}{1-1/x^2}\\ &=& \ln\frac{2}{1}=\ln 2\end{eqnarray*}
\vskip 2mm
d) \[ \ln\sqrt{x^4-1}+\ln\frac{1}{x^2}=\ln\frac{\sqrt{x^4-1}}{x^2}= \ln\sqrt{\frac{x^4-1}{x^4}}=\ln\sqrt{1-\frac{1}{x^4}}\] Detta går mot $\ln 1=0$ då $x\to-\infty$.
\vskip 2mm
e) Täljaren går mot $¹/2$, så gränsvärdet är 0.
\vskip 2mm
f) Till att börja med har vi \[ \frac{\sin x}{\tan^2x}=\frac{\sin x\cos^2x}{\sin^2x}=\frac{\cos^2x}{\sin x},\] så vi skall undersöka $(x-¹)\cos^2x/\sin x$ då $x\to ¹$. Faktorn $\cos^2x$ går mot $\cos^2¹=(-1)^2=1$. Sätt $t=x-¹$ så att $t\to 0$ då $x\to ¹$. Vi har $\sin x=\sin (t+¹)=-\sin t$, så $(x-¹)/\sin x=t/(-\sin t)\to -1$ då $t\to 0$. Gränsvärdet är således $-1$.
\vskip 2mm
5.16.a) Eftersom $2^n/3^n=(2/3)^n$ och $-1<2/3<1$ så är gränsvärdet 0.
\vskip 2mm
b) Omskrivningen \[ \frac{n}{n-1/\sqrt n}=\frac{1}{1-1/n\sqrt n}\] visar att gränsvärdet är $1/(1-0)=1$.
\vskip 2mm
e) Använd att $\lim_{n\to\infty}(1+x/n)^n=e^x$.
\vskip 2mm
f) Observera att $(1+2/n)^{3n}=((1+2/n)^n)^3$. Gränsvärdet blir $(e^2)^3=e^6$.

