Lösningar 12
Matematik för naturvetare 15hp
| Versionen från 2 oktober 2007 kl. 12.10 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Versionen från 2 oktober 2007 kl. 12.21 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 4: | Rad 4: | ||
| - | 5.10. Vi har \[ | + | '''5.10.''' |
| - | \lim_{x\to 1_{-}}f(x)=\lim_{x\to 1_{-}} ax=a\quad\mbox{och}\quad | + | |
| - | \lim_{x\to 1_{+}}f(x)=\lim_{x\to 1_{+}}(x^2-1)=1^2-1=0.\] | + | Vi har |
| + | |||
| + | |||
| + | <math> | ||
| + | \lim\_{x\to 1_{-}}f(x)=\lim_{x\to 1_{-}} ax=a\quad\mbox{och}\quad | ||
| + | \lim_{x\to 1_{+}}f(x)=\lim_{x\to 1_{+}}(x^2-1)=1^2-1=0</math> | ||
| + | |||
| + | |||
| + | |||
| För kontinuitet krävs att de två gränsvärdena är lika, vilket ger | För kontinuitet krävs att de två gränsvärdena är lika, vilket ger | ||
| villkoret $a=0$. | villkoret $a=0$. | ||
| - | \vskip 2mm | ||
| - | 5.12. Funktionen är inte definierad för $x=-1$ eftersom nämnaren blir | + | |
| + | '''5.12.''' | ||
| + | |||
| + | Funktionen är inte definierad för $x=-1$ eftersom nämnaren blir | ||
| 0 där. Absolutbeloppstecknet får man hantera genom att dela upp i | 0 där. Absolutbeloppstecknet får man hantera genom att dela upp i | ||
| olika intervall. Vi har $x^2-1> 0$ fö $x>1$ och $x<-1$ och | olika intervall. Vi har $x^2-1> 0$ fö $x>1$ och $x<-1$ och | ||
| - | $x^2-1<0$ för $-1<x<1$. Funktionen kan därför skrivas \[ | + | $x^2-1<0$ för $-1<x<1$. Funktionen kan därför skrivas |
| + | |||
| + | |||
| + | <math> | ||
| f(x)=\left\{\begin{array}{ll} | f(x)=\left\{\begin{array}{ll} | ||
| \frac{x^2-1}{x+1}=x-1 & \mbox{för $x<-1$ och $x>1$}\\ \\ | \frac{x^2-1}{x+1}=x-1 & \mbox{för $x<-1$ och $x>1$}\\ \\ | ||
| \frac{-(x^2-1)}{x+1}=-(x-1)=1-x & \mbox{för | \frac{-(x^2-1)}{x+1}=-(x-1)=1-x & \mbox{för | ||
| - | $-1<x<1$}\end{array}\right.\] | + | $-1<x<1$}\end{array}\right</math> |
| + | |||
| + | |||
| + | |||
| Eftersom $f$ inte är definierad för $x=-1$ så är detta en | Eftersom $f$ inte är definierad för $x=-1$ så är detta en | ||
| diskontinuitetspunkt och frågan är om den är hävbar, dvs om det går | diskontinuitetspunkt och frågan är om den är hävbar, dvs om det går | ||
| att definiera $f(-1)$ så att funktionen blir kontinuerlig. För detta | att definiera $f(-1)$ så att funktionen blir kontinuerlig. För detta | ||
| krävs att vänster- och högergränsvärdena då $x\to -1$ är lika. Vi har | krävs att vänster- och högergränsvärdena då $x\to -1$ är lika. Vi har | ||
| - | \[ | + | |
| + | |||
| + | |||
| + | <math> | ||
| \lim_{x\to -1_{-}}f(x)=\lim_{x\to | \lim_{x\to -1_{-}}f(x)=\lim_{x\to | ||
| -1_{-}}(x-1)=-1-1=-2\] | -1_{-}}(x-1)=-1-1=-2\] | ||
| och | och | ||
| - | \[\lim_{x\to -1_{+}}f(x)=\lim_{x\to -1_{+}}(1-x)=1-(-1)=2.\] | + | \[\lim_{x\to -1_{+}}f(x)=\lim_{x\to -1_{+}}(1-x)=1-(-1)=2 |
| + | </math> | ||
| + | |||
| + | |||
| + | |||
| Då gränsvärdena är olika så är diskontinuiteten inte hävbar. En annan | Då gränsvärdena är olika så är diskontinuiteten inte hävbar. En annan | ||
| - | möjlig diskontinuitetspunkt är $x=1$. Vi har \[ | + | möjlig diskontinuitetspunkt är $x=1$. Vi har |
| + | |||
| + | |||
| + | <math> | ||
| \lim_{x\to 1_{-}}f(x)=\lim_{x\to 1_{-}}(1-x)=0,\quad | \lim_{x\to 1_{-}}f(x)=\lim_{x\to 1_{-}}(1-x)=0,\quad | ||
| - | \lim_{x\to 1_{+}}f(x)=\lim_{x\to 1_{+}}(x-1)=0.\] | + | \lim_{x\to 1_{+}}f(x)=\lim_{x\to 1_{+}}(x-1)=0</math> |
| + | |||
| + | |||
| + | |||
| Alltså är $f$ kontinuerlig för $x=1$. Grafen finns i boken. | Alltså är $f$ kontinuerlig för $x=1$. Grafen finns i boken. | ||
| - | \vskip 2mm | ||
| - | 5.14.b) Vi har $y\to 0$ då $x\to±\infty$, så $x$-axeln (linjen $y=0$) | + | |
| + | '''5.14.b)''' | ||
| + | |||
| + | Vi har $y\to 0$ då $x\to±\infty$, så $x$-axeln (linjen $y=0$) | ||
| är en vågrät asymptot. Eftersom $x^2-1=(x-1)(x+1)$ så är linjerna $x=±1$ | är en vågrät asymptot. Eftersom $x^2-1=(x-1)(x+1)$ så är linjerna $x=±1$ | ||
| lodräta asymptoter. | lodräta asymptoter. | ||
| - | \vskip 2mm | ||
| - | c) Här gäller $y\to 1$ då $x\to±\infty$, så linjen $y=1$ är en vågrät | + | |
| + | '''5.14.c)''' | ||
| + | |||
| + | Här gäller $y\to 1$ då $x\to±\infty$, så linjen $y=1$ är en vågrät | ||
| asymptot. Nämnaren $x^2+1$ har inga (reella) nollställen, så lodräta | asymptot. Nämnaren $x^2+1$ har inga (reella) nollställen, så lodräta | ||
| asymptoter saknas. | asymptoter saknas. | ||
| - | \vskip 2mm | ||
| - | d) Eftersom $x^2-1=(x-1)(x+1)$ så skulle man kunna tro att linjerna | + | |
| + | '''5.14.d)''' | ||
| + | |||
| + | Eftersom $x^2-1=(x-1)(x+1)$ så skulle man kunna tro att linjerna | ||
| $x=±1$ är lodräta asymptoter. Men vi har $x^3+1=(x+1)(x^2-x+1)$, så | $x=±1$ är lodräta asymptoter. Men vi har $x^3+1=(x+1)(x^2-x+1)$, så | ||
| för $x\not=-1$ är $y=(x^2-x+1)/(x-1)$, varav framgår att det bara | för $x\not=-1$ är $y=(x^2-x+1)/(x-1)$, varav framgår att det bara | ||
| Rad 57: | Rad 92: | ||
| sneda asymptoter kan försöka visa att linjen $y=x$ är en sådan.) | sneda asymptoter kan försöka visa att linjen $y=x$ är en sådan.) | ||
| - | \vskip 2mm | ||
| - | e) Ledning: Nämnarens nollställen är 2 och $-3$. | ||
| - | \vskip 2mm | + | '''5.14.e)''' |
| + | |||
| + | Ledning: Nämnarens nollställen är 2 och $-3$. | ||
| + | |||
| + | |||
| + | |||
| + | '''5.14.f)''' | ||
| - | f) Ledning: Nämnarens nollställen är 1 och 2. | + | Ledning: Nämnarens nollställen är 1 och 2. |
Versionen från 2 oktober 2007 kl. 12.21
Lösningar till några övningar till lektion 12
5.10.
Vi har
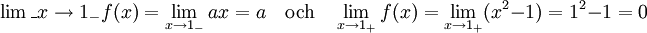
För kontinuitet krävs att de två gränsvärdena är lika, vilket ger villkoret $a=0$.
5.12.
Funktionen är inte definierad för $x=-1$ eftersom nämnaren blir 0 där. Absolutbeloppstecknet får man hantera genom att dela upp i olika intervall. Vi har $x^2-1> 0$ fö $x>1$ och $x<-1$ och $x^2-1<0$ för $-1<x<1$. Funktionen kan därför skrivas
Misslyckades med att tolka formel. (okänt fel): f(x)=\left\{\begin{array}{ll} \frac{x^2-1}{x+1}=x-1 & \mbox{för $x<-1$ och $x>1$}\\ \\ \frac{-(x^2-1)}{x+1}=-(x-1)=1-x & \mbox{för $-1<x<1$}\end{array}\right
Eftersom $f$ inte är definierad för $x=-1$ så är detta en
diskontinuitetspunkt och frågan är om den är hävbar, dvs om det går
att definiera $f(-1)$ så att funktionen blir kontinuerlig. För detta
krävs att vänster- och högergränsvärdena då $x\to -1$ är lika. Vi har
Misslyckades med att tolka formel. (okänt fel): \lim_{x\to -1_{-}}f(x)=\lim_{x\to -1_{-}}(x-1)=-1-1=-2\] och \[\lim_{x\to -1_{+}}f(x)=\lim_{x\to -1_{+}}(1-x)=1-(-1)=2
Då gränsvärdena är olika så är diskontinuiteten inte hävbar. En annan
möjlig diskontinuitetspunkt är $x=1$. Vi har
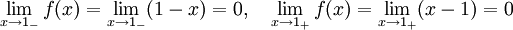
Alltså är $f$ kontinuerlig för $x=1$. Grafen finns i boken.
5.14.b)
Vi har $y\to 0$ då $x\to±\infty$, så $x$-axeln (linjen $y=0$) är en vågrät asymptot. Eftersom $x^2-1=(x-1)(x+1)$ så är linjerna $x=±1$ lodräta asymptoter.
5.14.c)
Här gäller $y\to 1$ då $x\to±\infty$, så linjen $y=1$ är en vågrät asymptot. Nämnaren $x^2+1$ har inga (reella) nollställen, så lodräta asymptoter saknas.
5.14.d)
Eftersom $x^2-1=(x-1)(x+1)$ så skulle man kunna tro att linjerna $x=±1$ är lodräta asymptoter. Men vi har $x^3+1=(x+1)(x^2-x+1)$, så för $x\not=-1$ är $y=(x^2-x+1)/(x-1)$, varav framgår att det bara är $x=1$ som är lodrät asymptot. För $x=-1$ har funktionen en hävbar diskontinuitet. Någon vågrät asymptot finns inte, eftersom $y\to ±\infty$ då $x\to±\infty$. (Den som läste anmärkningen ovan om sneda asymptoter kan försöka visa att linjen $y=x$ är en sådan.)
5.14.e)
Ledning: Nämnarens nollställen är 2 och $-3$.
5.14.f)
Ledning: Nämnarens nollställen är 1 och 2.

