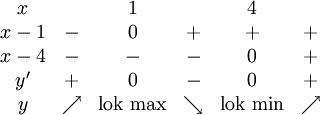Lösningar 14
Matematik för naturvetare 15hp
| Versionen från 16 oktober 2007 kl. 07.43 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (16 oktober 2007 kl. 08.34) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) |
||
| (11 mellanliggande versioner visas inte.) | |||
| Rad 5: | Rad 5: | ||
| - | 6.14.<math> | + | '''6.14.''' |
| + | |||
| + | <math> | ||
| h\frac{dM}{dh}=h\cdot 90\cdot 3h^2=3\cdot 90h^3=3M</math> | h\frac{dM}{dh}=h\cdot 90\cdot 3h^2=3\cdot 90h^3=3M</math> | ||
| - | 6.15. Med $V=V(r)=4\epsilon (\sigma^{12}r^{-12}-\sigma^6r^{-6})$ får | + | '''6.15.''' |
| - | vi <math> | + | |
| + | Med $V=V(r)=4\epsilon (\sigma^{12}r^{-12}-\sigma^6r^{-6})$ får | ||
| + | vi | ||
| + | |||
| + | <math> | ||
| F=-\frac{dV}{dr}=-4\epsilon (\sigma^{12}(-12r^{-13})-\sigma^6 | F=-\frac{dV}{dr}=-4\epsilon (\sigma^{12}(-12r^{-13})-\sigma^6 | ||
| (-6r^{-7}))= | (-6r^{-7}))= | ||
| -4\epsilon\left(\frac{6\sigma^6}{r^7}-\frac{12\sigma^{12}}{r^{13}}\right)</math> | -4\epsilon\left(\frac{6\sigma^6}{r^7}-\frac{12\sigma^{12}}{r^{13}}\right)</math> | ||
| - | När $F=0$ så måste parentesen vara 0, vilket ger <math> | + | |
| + | |||
| + | När $F=0$ så måste parentesen vara 0, vilket ger | ||
| + | |||
| + | <math> | ||
| \frac{6\sigma^6}{r^7}=\frac{12\sigma^{12}}{r^{13}} | \frac{6\sigma^6}{r^7}=\frac{12\sigma^{12}}{r^{13}} | ||
| \quad\mbox{dvs}\quad | \quad\mbox{dvs}\quad | ||
| r^6=2\sigma^6</math> | r^6=2\sigma^6</math> | ||
| + | |||
| + | |||
| Villkoret är alltså $r=2^{1/6} \sigma$. | Villkoret är alltså $r=2^{1/6} \sigma$. | ||
| - | 6.16. Medelhastigheten för tillväxten mellan tidpunkterna $t_{1}$ och | + | '''6.16.''' |
| - | $t_{2}$ är <math> | + | |
| - | \frac{H(t_{2})-H(t_{1})}{t_{2}-t_{1}}.</math> | + | Medelhastigheten för tillväxten mellan tidpunkterna $t_{1}$ och |
| - | Medelhastigheten mellan 4:e och 6:e veckan blir <math> | + | $t_{2}$ är |
| + | |||
| + | <math> | ||
| + | \frac{H(t_{2})-H(t_{1})}{t_{2}-t_{1}} | ||
| + | </math> | ||
| + | |||
| + | Medelhastigheten mellan 4:e och 6:e veckan blir | ||
| + | |||
| + | <math> | ||
| \frac{H(6)-H(4)}{6-4}=\frac{6^2/4+6-(4^2/4+4)}{6-4}= | \frac{H(6)-H(4)}{6-4}=\frac{6^2/4+6-(4^2/4+4)}{6-4}= | ||
| \frac{15-8}{2}=3,5\quad\mbox{mm per vecka}</math> | \frac{15-8}{2}=3,5\quad\mbox{mm per vecka}</math> | ||
| + | |||
| + | |||
| Tillväxthastigheten när vecka 5 börjar är $H'(5)=5/2+1=3,5$ mm per | Tillväxthastigheten när vecka 5 börjar är $H'(5)=5/2+1=3,5$ mm per | ||
| vecka. Att värdena blir desamma beror på att tangenten i $t=5$ är | vecka. Att värdena blir desamma beror på att tangenten i $t=5$ är | ||
| Rad 35: | Rad 57: | ||
| - | 6.18. Löser vi ut $T$ så får vi $T(V)=kV^{-0,4}$ och alltså | + | '''6.18.''' |
| - | $T'(V)=-0,4kV^{-1,4}$. Alltså är <math> | + | |
| + | Löser vi ut $T$ så får vi $T(V)=kV^{-0,4}$ och alltså | ||
| + | $T'(V)=-0,4kV^{-1,4}$. Alltså är | ||
| + | |||
| + | <math> | ||
| \frac{V}{T}\cdot\frac{dT}{dV}=\frac{V}{kV^{-0,4}}\cdot | \frac{V}{T}\cdot\frac{dT}{dV}=\frac{V}{kV^{-0,4}}\cdot | ||
| (-0,4kV^{-1,4})=-0,4.</math> | (-0,4kV^{-1,4})=-0,4.</math> | ||
| - | Ett annat sätt är att logaritmera sambandet, $\ln T+0,4\ln V=\ln k$, | + | |
| - | och sedan derivera: <math> | + | |
| - | \frac{T'(V)}{T}+0,4\cdot\frac{1}{V}=0.</math> | + | Ett annat sätt är att först logaritmera sambandet: $\ln T=\ln k - 0,4\ln V$, |
| + | och sedan derivera: | ||
| + | |||
| + | <math> | ||
| + | \frac{T'(V)}{T}=-0,4\cdot\frac{1}{V}</math> | ||
| + | |||
| + | |||
| Detta ger efter omskrivning $VT'(V)/T=-0,4$. | Detta ger efter omskrivning $VT'(V)/T=-0,4$. | ||
| - | 6.19. Om $f(x_{0})=5$ så är $(f^{-1})'(5)=1/f'(x_{0})$. Vi måste | + | '''6.19.''' |
| + | |||
| + | Om $f(x_{0})=5$ så är $(f^{-1})'(5)=1/f'(x_{0})$. Vi måste | ||
| alltså lösa ekvationen $f(x_{0})=3-2x^5=5$. Vi får $x_{0}=-1$ och | alltså lösa ekvationen $f(x_{0})=3-2x^5=5$. Vi får $x_{0}=-1$ och | ||
| alltså $(f^{-1})'(5)=1/(-2\cdot 5(-1)^4)=-1/10$. | alltså $(f^{-1})'(5)=1/(-2\cdot 5(-1)^4)=-1/10$. | ||
| Rad 52: | Rad 86: | ||
| - | 6.20. Som i förra uppgiften måste vi lösa $f(x_{0})=3$. Vi får | + | '''6.20.''' |
| - | $x_{0}=5$ och eftersom <math> | + | |
| + | Som i förra uppgiften måste vi lösa $f(x_{0})=3$. Vi får | ||
| + | $x_{0}=5$ och eftersom | ||
| + | |||
| + | <math> | ||
| f'(x)=\frac{1(x-2)-1(x+4)}{(x-2)^2}=-\frac{6}{(x-2)^2}</math> | f'(x)=\frac{1(x-2)-1(x+4)}{(x-2)^2}=-\frac{6}{(x-2)^2}</math> | ||
| + | |||
| + | |||
| så får vi $(f^{-1})'(3)=1/f'(5)=-(5-2)^2/6=-3/2$. | så får vi $(f^{-1})'(3)=1/f'(5)=-(5-2)^2/6=-3/2$. | ||
| - | 6.24. Derivering av sambandet $x^2-y^2=8$ ger $2x-2yy'=0$, varav | + | '''6.24.''' |
| + | |||
| + | Derivering av sambandet $x^2-y^2=8$ ger $2x-2yy'=0$, varav | ||
| $y'=x/y$. Alltså är $y'(3)=3/1=3$. Tangentens ekvation är | $y'=x/y$. Alltså är $y'(3)=3/1=3$. Tangentens ekvation är | ||
| $y-1=3(x-3)$ eller $y=3x-8$. | $y-1=3(x-3)$ eller $y=3x-8$. | ||
| Rad 65: | Rad 107: | ||
| - | 6.27.b) Om funktionen betecknas med $f$ så är <math> | + | '''6.27.b)''' |
| + | |||
| + | Om funktionen betecknas med $f$ så är | ||
| + | |||
| + | <math> | ||
| \ln |f(x)|=2\ln|\sin x|+3\ln|\cos x|-\ln|\sin 3x|-2\ln|\cos 2x|</math> | \ln |f(x)|=2\ln|\sin x|+3\ln|\cos x|-\ln|\sin 3x|-2\ln|\cos 2x|</math> | ||
| - | och deriverar vi detta så får vi <math> | + | |
| + | |||
| + | och deriverar vi detta så får vi | ||
| + | |||
| + | <math> | ||
| \frac{f'(x)}{f(x)}=\frac{2\cos x}{\sin x}-\frac{3\sin x}{\cos | \frac{f'(x)}{f(x)}=\frac{2\cos x}{\sin x}-\frac{3\sin x}{\cos | ||
| x}-\frac{3\cos 3x}{\sin 3x}+\frac{4\sin 2x}{\cos 2x}= | x}-\frac{3\cos 3x}{\sin 3x}+\frac{4\sin 2x}{\cos 2x}= | ||
| - | \frac{2}{\tan x}-3\tan x-\frac{3}{\tan 3x}+4\tan 2x.</math> | + | \frac{2}{\tan x}-3\tan x-\frac{3}{\tan 3x}+4\tan 2x</math> |
| + | |||
| + | |||
| Multiplikation av båda leden med $f(x)$ ger resultatet. | Multiplikation av båda leden med $f(x)$ ger resultatet. | ||
| - | c) Om $f(x)=x^3e^{\sin x}$ så är $\ln|f(x)|=3\ln |x|+\sin x$, så <math> | + | '''6.27.c)''' |
| + | |||
| + | Om $f(x)=x^3e^{\sin x}$ så är $\ln|f(x)|=3\ln |x|+\sin x$, så | ||
| + | |||
| + | <math> | ||
| \frac{f'(x)}{f(x)}=\frac{3}{x}+\cos x.</math> | \frac{f'(x)}{f(x)}=\frac{3}{x}+\cos x.</math> | ||
| - | d) Med $f(x)=x^{\cos x}$ så är $\ln|f(x)|=\cos x\ln|x|$, alltså <math> | + | '''6.27.d)''' |
| + | |||
| + | Med $f(x)=x^{\cos x}$ så är $\ln|f(x)|=\cos x\ln|x|$, alltså | ||
| + | |||
| + | <math> | ||
| f'(x)=-\sin x\ln |x|+\frac{\cos x}{x}.</math> | f'(x)=-\sin x\ln |x|+\frac{\cos x}{x}.</math> | ||
| - | 7.1, 7.2.a) Derivatan är $y'=3x^2-12x+9=3(x^2-4x+3)$ med nollställena | + | '''7.1, 7.2.a)''' |
| + | |||
| + | Derivatan är $y'=3x^2-12x+9=3(x^2-4x+3)$ med nollställena | ||
| $x=2±\sqrt{2^2-3}=2±1$, alltså 1 och 3. Enligt faktorsatsen är | $x=2±\sqrt{2^2-3}=2±1$, alltså 1 och 3. Enligt faktorsatsen är | ||
| - | $y'=3(x-1)(x-3)$. Vi gör ett teckenschema:<math>\begin{array}{cccccccccc} | + | $y'=3(x-1)(x-3)$. Vi gör ett teckenschema: |
| - | x & & 1 & & 3 \\ | + | |
| - | \hline \\ | + | |
| + | <math>\begin{array}{cccccc} | ||
| + | x & & 1 & & 3 &\\ | ||
| 3 & + & + & + & + & + \\ | 3 & + & + & + & + & + \\ | ||
| x-1 & - & 0 & + & + & + \\ | x-1 & - & 0 & + & + & + \\ | ||
| Rad 96: | Rad 160: | ||
| y &\nearrow &\mbox{lok max} &\searrow &\mbox{lok min} | y &\nearrow &\mbox{lok max} &\searrow &\mbox{lok min} | ||
| &\nearrow\end{array}</math> | &\nearrow\end{array}</math> | ||
| + | |||
| + | |||
| (Det är ju egentligen onödigt att ta med faktorn 3 i schemat, eftersom | (Det är ju egentligen onödigt att ta med faktorn 3 i schemat, eftersom | ||
| den är positiv överallt och därför inte kan påverka tecknet. Hade det | den är positiv överallt och därför inte kan påverka tecknet. Hade det | ||
| Rad 103: | Rad 169: | ||
| - | c) Skriver vi $y=1+1/x$ så ser vi genast att funktionen är avtagande | + | '''7.2.c)''' |
| + | |||
| + | Skriver vi $y=1+1/x$ så ser vi genast att funktionen är avtagande | ||
| överallt där den är definierad, dvs för $x\not=0$. Derivatan är | överallt där den är definierad, dvs för $x\not=0$. Derivatan är | ||
| $y'=-1/x^2$, som ju mycket riktigt är $<0$ för alla $x\not=0$. | $y'=-1/x^2$, som ju mycket riktigt är $<0$ för alla $x\not=0$. | ||
| Rad 109: | Rad 177: | ||
| - | e) Derivatan är $y'=2/x-2x=2(1-x^2)/x=-2(x+1)(x-1)/x$. Funktionen är | + | '''7.2.e)''' |
| + | |||
| + | Derivatan är $y'=2/x-2x=2(1-x^2)/x=-2(x+1)(x-1)/x$. Funktionen är | ||
| definierad bara för $x>0$ och i det området är $(x+1)/x>0$. | definierad bara för $x>0$ och i det området är $(x+1)/x>0$. | ||
| - | Teckenschemat blir alltså ganska enkelt:<math>\begin{array}{cccccccccc} | + | Teckenschemat blir alltså ganska enkelt: |
| - | x & & 1 \\ | + | |
| - | \hline\\ | + | |
| + | <math>\begin{array}{cccc} | ||
| + | x & & 1 &\\ | ||
| -2 & - & - & - \\ | -2 & - & - & - \\ | ||
| x-1 & - & 0 & + \\ | x-1 & - & 0 & + \\ | ||
| Rad 121: | Rad 193: | ||
| - | g) Derivatan är <math> | + | '''7.2.g)''' |
| - | y'=e^x(x^2-2x+2)+e^x(2x-2)=x^2e^x</math> | + | |
| + | Derivatan är | ||
| + | |||
| + | <math> | ||
| + | y'=e^x(x^2-2x+2)+e^x(2x-2)=x^2e^x | ||
| + | </math> | ||
| + | |||
| + | |||
| som är $>0$ för $x\not =0$ och 0 för $x=0$. Alltså är funktionen | som är $>0$ för $x\not =0$ och 0 för $x=0$. Alltså är funktionen | ||
| strängt avtagande och $x=0$ en terrasspunkt. | strängt avtagande och $x=0$ en terrasspunkt. | ||
| Rad 128: | Rad 207: | ||
| - | 7.4.a) Derivatan är $y'=8x^3+1$ som har ett nollställe $x=-1/2$. | + | '''7.4.a)''' |
| + | |||
| + | Derivatan är $y'=8x^3+1$ som har ett nollställe $x=-1/2$. | ||
| Enligt faktorsatsen är $8x^3+1$ delbart med $x-(-1/2)=x+1/2$, dvs | Enligt faktorsatsen är $8x^3+1$ delbart med $x-(-1/2)=x+1/2$, dvs | ||
| även med $2x+1$ och utför vi divisionen så får vi | även med $2x+1$ och utför vi divisionen så får vi | ||
| Rad 137: | Rad 218: | ||
| - | d) Derivatan är $y'=4-4x-3x^2$ med nollställena $x=-2$ och $x=2/3$. | + | '''7.4.d)''' |
| + | |||
| + | Derivatan är $y'=4-4x-3x^2$ med nollställena $x=-2$ och $x=2/3$. | ||
| Alltså är $y'=(-3)(x^2+4x/3-4/3)=(-3)(x-(-2))(x-2/3)=(-3)(x+2)(x-2/3)$. | Alltså är $y'=(-3)(x^2+4x/3-4/3)=(-3)(x-(-2))(x-2/3)=(-3)(x+2)(x-2/3)$. | ||
| - | Teckenschemat se ut så här:<math>\begin{array}{ccccccccccccc} | + | Teckenschemat se ut så här: |
| - | x & & -2& & 2/3 \\ | + | |
| - | \hline \\ | + | |
| + | <math>\begin{array}{cccccc} | ||
| + | x & & -2& & 2/3 &\\ | ||
| -3 & - & - & - & - & - \\ | -3 & - & - & - & - & - \\ | ||
| x+2& - & 0 & + & + & + \\ | x+2& - & 0 & + & + & + \\ | ||
| Rad 151: | Rad 236: | ||
| - | 7.5.b) En funktion $f(x)=g(x)^2$ som är kvadraten på | + | |
| + | '''7.5.b)''' | ||
| + | |||
| + | En funktion $f(x)=g(x)^2$ som är kvadraten på | ||
| en annan funktion kan man derivera antingen genom att använda | en annan funktion kan man derivera antingen genom att använda | ||
| produktregeln eller genom att använda kedjeregeln. Det första sättet | produktregeln eller genom att använda kedjeregeln. Det första sättet | ||
| Rad 157: | Rad 245: | ||
| $f'(x)=2g(x)\cdot g'(x)$ eftersom den inre derivatan är $g'(x)$. Med | $f'(x)=2g(x)\cdot g'(x)$ eftersom den inre derivatan är $g'(x)$. Med | ||
| $g(x)=\sin x$ ger detta $f'(x)=2\sin x\cos x=\sin 2x$. Lösningarna till | $g(x)=\sin x$ ger detta $f'(x)=2\sin x\cos x=\sin 2x$. Lösningarna till | ||
| - | ekvationen $\sin 2x=0$ är $2x=n¹$, dvs $x=n¹/2$, där $n=0,±1,±2,\ldots$. | + | ekvationen $\sin 2x=0$ är $2x=n\pi$, dvs $x=n\pi/2$, där $n=0,±1,±2,\ldots$. |
| Teckenväxlingen är $-0+$ när $n$ är jämnt och $+0-$ då $n$ är udda. | Teckenväxlingen är $-0+$ när $n$ är jämnt och $+0-$ då $n$ är udda. | ||
| - | För $n=2m$, dvs $x=m¹$, har vi således lokala minima och för $n=2m+1$, | + | För $n=2m$, dvs $x=m\pi$, har vi således lokala minima och för $n=2m+1$, |
| - | dvs $x=¹/2+m¹$, har vi lokala maxima. | + | dvs $x=\pi/2+m\pi$, har vi lokala maxima. |
| - | d) Derivatan är $y'=(e^x-e^{-x})/2$ som har ett enda nollställe | + | '''7.5.d)''' |
| + | |||
| + | Derivatan är $y'=(e^x-e^{-x})/2$ som har ett enda nollställe | ||
| $x=0$. Teckenväxligen är $-0+$, varför detta är ett lokalt minimum. | $x=0$. Teckenväxligen är $-0+$, varför detta är ett lokalt minimum. | ||
| - | 7.7.a) Vi börjar med att undersöka funktionens nollställen och | + | '''7.7.a)''' |
| + | |||
| + | Vi börjar med att undersöka funktionens nollställen och | ||
| tecken (sådan information är alltid användbar när man skall rita | tecken (sådan information är alltid användbar när man skall rita | ||
| grafer). Vi har förstås $y=0$ för $x=0$ och $x=-1$. Eftersom | grafer). Vi har förstås $y=0$ för $x=0$ och $x=-1$. Eftersom | ||
| - | $y=x(x+1)$ så får vi teckenschemat <math>\begin{array}{ccccccccc} | + | $y=x(x+1)$ så får vi teckenschemat |
| - | x & & -1 & & 0 \\ | + | |
| - | \hline\\ | + | |
| + | <math>\begin{array}{cccccc} | ||
| + | x & & -1 & & 0 &\\ | ||
| x+1 & - & 0 & + & + & + \\ | x+1 & - & 0 & + & + & + \\ | ||
| x & - & - & - & 0 & + \\ | x & - & - & - & 0 & + \\ | ||
| y & + & 0 & - & 0 & + | y & + & 0 & - & 0 & + | ||
| \end{array}</math> | \end{array}</math> | ||
| + | |||
| + | |||
| Vi har $y=x^2+x=x^2(1+1/x)$, vilket visar att $y\to\infty$ då | Vi har $y=x^2+x=x^2(1+1/x)$, vilket visar att $y\to\infty$ då | ||
| $x\to±\infty$. Derivatan är $y'=2x+1$ som är 0 för $x=-1/2$. | $x\to±\infty$. Derivatan är $y'=2x+1$ som är 0 för $x=-1/2$. | ||
| Rad 184: | Rad 280: | ||
| Inga asymptoter finns. | Inga asymptoter finns. | ||
| Anmärkning: Ett annat sätt är förstås att kvadratkomplettera, vilket | Anmärkning: Ett annat sätt är förstås att kvadratkomplettera, vilket | ||
| - | ger <math> | + | ger |
| + | |||
| + | <math> | ||
| y=x^2+x=x^2+2\cdot \frac{1}{2}\cdot x+\left(\frac{1}{2}\right)^2- | y=x^2+x=x^2+2\cdot \frac{1}{2}\cdot x+\left(\frac{1}{2}\right)^2- | ||
| \left(\frac{1}{2}\right)^2=\left(x+\frac{1}{2}\right)^2- | \left(\frac{1}{2}\right)^2=\left(x+\frac{1}{2}\right)^2- | ||
| - | \frac{1}{4}.</math> | + | \frac{1}{4}</math> |
| + | |||
| + | |||
| Här ser vi direkt att $y$ har ett lokalt minimum för $x=-1/2$ och | Här ser vi direkt att $y$ har ett lokalt minimum för $x=-1/2$ och | ||
| värdet är $-1/4$. | värdet är $-1/4$. | ||
| Rad 193: | Rad 293: | ||
| - | c) Lägg först märke till att funktionen inte är definierad för | + | '''7.7.c)''' |
| + | |||
| + | Lägg först märke till att funktionen inte är definierad för | ||
| $x=-2$. Vi har $y\to 0$ då $x\to\infty$, så $x$-axeln är en vågrät asymptot. | $x=-2$. Vi har $y\to 0$ då $x\to\infty$, så $x$-axeln är en vågrät asymptot. | ||
| Vidare gäller $y\to±\infty$ då $x\to -2_{±}$, så linjen $x=-2$ är en | Vidare gäller $y\to±\infty$ då $x\to -2_{±}$, så linjen $x=-2$ är en | ||
| Rad 202: | Rad 304: | ||
| - | d) Funktionen har ett enda nollställe $x=0$. Nämnaren är 0 för $x=1$ | + | '''7.7.d)''' |
| + | |||
| + | Funktionen har ett enda nollställe $x=0$. Nämnaren är 0 för $x=1$ | ||
| och där är funktionen således inte definierad. Vi har | och där är funktionen således inte definierad. Vi har | ||
| $x^3-1=(x-1)(x^2+x+1)$, där polynomet $x^2+x+1=(x+1/2)^2+3/4$ är positivt | $x^3-1=(x-1)(x^2+x+1)$, där polynomet $x^2+x+1=(x+1/2)^2+3/4$ är positivt | ||
| för alla $x$. Alltså är $y<0$ då $x<1$ och $y>0$ då $x>1$. | för alla $x$. Alltså är $y<0$ då $x<1$ och $y>0$ då $x>1$. | ||
| - | Omskrivningen <math> | + | Omskrivningen |
| + | |||
| + | <math> | ||
| y=\frac{x^2}{x^3-1}=\frac{1/x}{1-1/x^3}</math> | y=\frac{x^2}{x^3-1}=\frac{1/x}{1-1/x^3}</math> | ||
| + | |||
| + | |||
| visar att $y\to 0$ då $x\to±\infty$, varför $x$-axeln är en vågrät asymptot. | visar att $y\to 0$ då $x\to±\infty$, varför $x$-axeln är en vågrät asymptot. | ||
| Linjen $x=1$ är en lodrät asymptot eftersom $y\to±\infty$ då $x\to | Linjen $x=1$ är en lodrät asymptot eftersom $y\to±\infty$ då $x\to | ||
| - | 1_{±}$. Vi deriverar: <math> | + | 1_{±}$. Vi deriverar: |
| + | |||
| + | <math> | ||
| y'=\frac{2x(x^3-1)-x^2\cdot 3x^2}{(x^3-1)^2}=\frac{-x^4-2x}{(x^3-1)^2}= | y'=\frac{2x(x^3-1)-x^2\cdot 3x^2}{(x^3-1)^2}=\frac{-x^4-2x}{(x^3-1)^2}= | ||
| \frac{-x(x^3+2)}{(x^3-1)^2}</math> | \frac{-x(x^3+2)}{(x^3-1)^2}</math> | ||
| + | |||
| + | |||
| Derivatans nollställen är alltså 0 och $-\root3\of 2$. | Derivatans nollställen är alltså 0 och $-\root3\of 2$. | ||
| Nämnaren är $\ge 0$ för alla $x$, så den behöver vi inte ta med i | Nämnaren är $\ge 0$ för alla $x$, så den behöver vi inte ta med i | ||
| - | teckenschemat: <math>\begin{array}{ccccccccccc} | + | teckenschemat: |
| - | x & & -\root3\of 2 & & 0 \\ | + | |
| - | \hline\\ | + | |
| + | <math>\begin{array}{cccccc} | ||
| + | x & & - \sqrt[3]{2} & & 0 &\\ | ||
| -1 & - & - & - & - & - \\ | -1 & - & - & - & - & - \\ | ||
| x & - & - & - & 0 & + \\ | x & - & - & - & 0 & + \\ | ||
| Rad 223: | Rad 337: | ||
| y' & - & 0 & + & 0 & - \\ | y' & - & 0 & + & 0 & - \\ | ||
| y &\searrow &\mbox{lok min} & \searrow & \mbox{lok max} &\searrow \end{array}</math> | y &\searrow &\mbox{lok min} & \searrow & \mbox{lok max} &\searrow \end{array}</math> | ||
| + | |||
| + | |||
| Eventuellt kan man ta med punkten $x=1$ i teckenschemat, som en | Eventuellt kan man ta med punkten $x=1$ i teckenschemat, som en | ||
| påminnelse om att funktionen inte är definierad där. | påminnelse om att funktionen inte är definierad där. | ||
| Rad 228: | Rad 344: | ||
| - | f) Funktionen är inte definierad för $x=1$ och har ett enda | + | '''7.7.f)''' |
| - | nollställe $x=4/3$. Teckenschema för funktionen: <math> | + | |
| - | \begin{array}{ccccccccccccc} | + | Funktionen är inte definierad för $x=1$ och har ett enda |
| - | x & & 1 & & 4/3 \\ | + | nollställe $x=4/3$. Teckenschema för funktionen: |
| - | \hline\\ | + | |
| + | |||
| + | <math> | ||
| + | \begin{array}{cccccc} | ||
| + | x & & 1 & & 4/3 &\\ | ||
| 4-3x & + & + & + & 0 & - \\ | 4-3x & + & + & + & 0 & - \\ | ||
| 1-x & + & 0 & - & - & - \\ | 1-x & + & 0 & - & - & - \\ | ||
| y & + & \mbox{ej def.} & - & 0 & + | y & + & \mbox{ej def.} & - & 0 & + | ||
| \end{array}</math> | \end{array}</math> | ||
| + | |||
| + | |||
| Vi har $y\to\infty$ då $x\to 1_{-}$ och $y\to-\infty$ då $x\to | Vi har $y\to\infty$ då $x\to 1_{-}$ och $y\to-\infty$ då $x\to | ||
| 1_{+}$, så linjen $x=1$ är en lodrät asymptot. Förkortar vi uttrycket | 1_{+}$, så linjen $x=1$ är en lodrät asymptot. Förkortar vi uttrycket | ||
| - | för $y$ med $x$ så får vi <math> | + | för $y$ med $x$ så får vi |
| + | |||
| + | <math> | ||
| y=\frac{4/x-3}{1/x-1},</math> | y=\frac{4/x-3}{1/x-1},</math> | ||
| + | |||
| + | |||
| som går mot $(-3)/(-1)=3$ då $x\to±\infty$. Linjen $y=3$ är således en | som går mot $(-3)/(-1)=3$ då $x\to±\infty$. Linjen $y=3$ är således en | ||
| - | vågrät asymptot. Derivatan är <math> | + | vågrät asymptot. Derivatan är |
| - | y'=\frac{(-3)(1-x)-(-1)(4-3x)}{(1-x)^2}=\frac{1}{(1-x)^2},</math> | + | |
| + | <math> | ||
| + | y'=\frac{(-3)(1-x)-(-1)(4-3x)}{(1-x)^2}=\frac{1}{(1-x)^2}</math> | ||
| + | |||
| + | |||
| som saknar nollställen. Funktionen har därför inga lokala | som saknar nollställen. Funktionen har därför inga lokala | ||
| extremvärden. | extremvärden. | ||
| Rad 259: | Rad 389: | ||
| - | g) Eftersom $4-x^2=(2-x)(2+x)$ så är funktionen inte definierad för | + | '''7.7.g)''' |
| + | |||
| + | Eftersom $4-x^2=(2-x)(2+x)$ så är funktionen inte definierad för | ||
| $x=±2$. Den har ett enda nollställe för $x=5/2$. Vi börjar med att | $x=±2$. Den har ett enda nollställe för $x=5/2$. Vi börjar med att | ||
| göra ett teckenschema för | göra ett teckenschema för | ||
| - | $y=-(2x-5)/(x+2)(x-2)$:<math>\begin{array}{cccccccccccc} | + | $y=-(2x-5)/(x+2)(x-2)$: |
| - | x & & -2 & & 2 & & 5/2 \\ | + | |
| - | \hline \\ | + | |
| + | <math>\begin{array}{cccccccc} | ||
| + | x & & -2 & & 2 & & 5/2 & \\ | ||
| -1 & - & - & - & - & - & - & - \\ | -1 & - & - & - & - & - & - & - \\ | ||
| x+2 & - & 0 & + & + & + & + & + \\ | x+2 & - & 0 & + & + & + & + & + \\ | ||
| Rad 270: | Rad 404: | ||
| 2x-5& - & - & - & - & - & 0 & + \\ | 2x-5& - & - & - & - & - & 0 & + \\ | ||
| y & + &\mbox{ej def.} & - & \mbox{ej def.} & + & 0 & - \end{array}</math> | y & + &\mbox{ej def.} & - & \mbox{ej def.} & + & 0 & - \end{array}</math> | ||
| + | |||
| + | |||
| Eftersom täljaren har lägre grad än nämnaren, så gäller $y\to 0$ då | Eftersom täljaren har lägre grad än nämnaren, så gäller $y\to 0$ då | ||
| $x\to±\infty$. Alltså är $x$-axeln en vågrät asymptot. Lodräta | $x\to±\infty$. Alltså är $x$-axeln en vågrät asymptot. Lodräta | ||
| Rad 277: | Rad 413: | ||
| - | Derivatan är <math> | + | Derivatan är |
| + | |||
| + | <math> | ||
| y'=\frac{2(4-x^2)-(2x-5)(-2x)}{(4-x^2)^2}=\frac{2x^2-10x+8}{(4-x^2)^2}= | y'=\frac{2(4-x^2)-(2x-5)(-2x)}{(4-x^2)^2}=\frac{2x^2-10x+8}{(4-x^2)^2}= | ||
| \frac{2(x-1)(x-4)}{(4-x^2)^2}</math> | \frac{2(x-1)(x-4)}{(4-x^2)^2}</math> | ||
| + | |||
| + | |||
| som har nollställena $x=1$ och $x=4$. Nämnaren är $\ge 0$ för alla $x$ | som har nollställena $x=1$ och $x=4$. Nämnaren är $\ge 0$ för alla $x$ | ||
| och man behöver därför inte ta med den i teckenschemat, men man måste | och man behöver därför inte ta med den i teckenschemat, men man måste | ||
| ha i minnet att varken funktionen eller derivatan är definierad för | ha i minnet att varken funktionen eller derivatan är definierad för | ||
| - | $x=±2$.<math>\begin{array}{ccccccccccc} | + | $x=±2$. |
| - | x & & 1 & & 4 \\ | + | |
| - | \hline\\ | + | |
| + | <math>\begin{array}{cccccc} | ||
| + | x & & 1 & & 4 &\\ | ||
| x-1 & - & 0 & + & + & + \\ | x-1 & - & 0 & + & + & + \\ | ||
| x-4 & - & - & - & 0 & + \\ | x-4 & - & - & - & 0 & + \\ | ||
Nuvarande version
[redigera] Lösningar till några övningar till lektion 14
6.14.
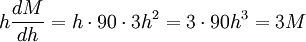
6.15.
Med $V=V(r)=4\epsilon (\sigma^{12}r^{-12}-\sigma^6r^{-6})$ får vi
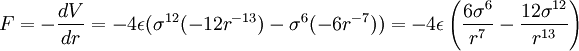
När $F=0$ så måste parentesen vara 0, vilket ger
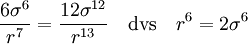
Villkoret är alltså $r=2^{1/6} \sigma$.
6.16.
Medelhastigheten för tillväxten mellan tidpunkterna $t_{1}$ och $t_{2}$ är
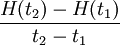
Medelhastigheten mellan 4:e och 6:e veckan blir
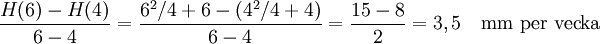
Tillväxthastigheten när vecka 5 börjar är $H'(5)=5/2+1=3,5$ mm per
vecka. Att värdena blir desamma beror på att tangenten i $t=5$ är
parallell med linjen genom $(4,H(4))$ och $(6,H(6))$.
6.18.
Löser vi ut $T$ så får vi $T(V)=kV^{-0,4}$ och alltså $T'(V)=-0,4kV^{-1,4}$. Alltså är
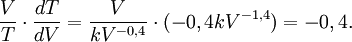
Ett annat sätt är att först logaritmera sambandet: $\ln T=\ln k - 0,4\ln V$,
och sedan derivera:
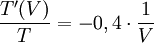
Detta ger efter omskrivning $VT'(V)/T=-0,4$.
6.19.
Om $f(x_{0})=5$ så är $(f^{-1})'(5)=1/f'(x_{0})$. Vi måste alltså lösa ekvationen $f(x_{0})=3-2x^5=5$. Vi får $x_{0}=-1$ och alltså $(f^{-1})'(5)=1/(-2\cdot 5(-1)^4)=-1/10$.
6.20.
Som i förra uppgiften måste vi lösa $f(x_{0})=3$. Vi får $x_{0}=5$ och eftersom
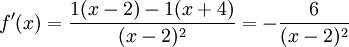
så får vi $(f^{-1})'(3)=1/f'(5)=-(5-2)^2/6=-3/2$.
6.24.
Derivering av sambandet $x^2-y^2=8$ ger $2x-2yy'=0$, varav $y'=x/y$. Alltså är $y'(3)=3/1=3$. Tangentens ekvation är $y-1=3(x-3)$ eller $y=3x-8$.
6.27.b)
Om funktionen betecknas med $f$ så är
ln | f(x) | = 2ln | sinx | + 3ln | cosx | − ln | sin3x | − 2ln | cos2x |
och deriverar vi detta så får vi
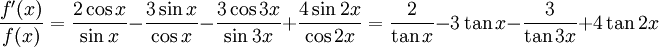
Multiplikation av båda leden med $f(x)$ ger resultatet.
6.27.c)
Om $f(x)=x^3e^{\sin x}$ så är $\ln|f(x)|=3\ln |x|+\sin x$, så
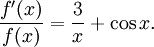
6.27.d)
Med $f(x)=x^{\cos x}$ så är $\ln|f(x)|=\cos x\ln|x|$, alltså
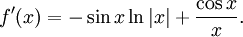
7.1, 7.2.a)
Derivatan är $y'=3x^2-12x+9=3(x^2-4x+3)$ med nollställena $x=2±\sqrt{2^2-3}=2±1$, alltså 1 och 3. Enligt faktorsatsen är $y'=3(x-1)(x-3)$. Vi gör ett teckenschema:
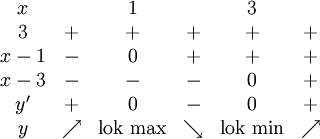
(Det är ju egentligen onödigt att ta med faktorn 3 i schemat, eftersom
den är positiv överallt och därför inte kan påverka tecknet. Hade det
i stället stått t ex $-3$, så hade det varit nödvändigt att ta med
den i schemat.)
7.2.c)
Skriver vi $y=1+1/x$ så ser vi genast att funktionen är avtagande överallt där den är definierad, dvs för $x\not=0$. Derivatan är $y'=-1/x^2$, som ju mycket riktigt är $<0$ för alla $x\not=0$.
7.2.e)
Derivatan är $y'=2/x-2x=2(1-x^2)/x=-2(x+1)(x-1)/x$. Funktionen är definierad bara för $x>0$ och i det området är $(x+1)/x>0$. Teckenschemat blir alltså ganska enkelt:

7.2.g)
Derivatan är
y' = ex(x2 − 2x + 2) + ex(2x − 2) = x2ex
som är $>0$ för $x\not =0$ och 0 för $x=0$. Alltså är funktionen
strängt avtagande och $x=0$ en terrasspunkt.
7.4.a)
Derivatan är $y'=8x^3+1$ som har ett nollställe $x=-1/2$. Enligt faktorsatsen är $8x^3+1$ delbart med $x-(-1/2)=x+1/2$, dvs även med $2x+1$ och utför vi divisionen så får vi $y'=(2x+1)(4x^2-2x+1)$. Den andra faktorn är $>0$ för alla $x$, så $y'<0$ för $x<-1/2$ och $y'>0$ för $x>-1/2$. Alltså är $x=-1/2$ ett lokalt minimum och vi har $y(-1/2)=-19/8$.
7.4.d)
Derivatan är $y'=4-4x-3x^2$ med nollställena $x=-2$ och $x=2/3$. Alltså är $y'=(-3)(x^2+4x/3-4/3)=(-3)(x-(-2))(x-2/3)=(-3)(x+2)(x-2/3)$. Teckenschemat se ut så här:
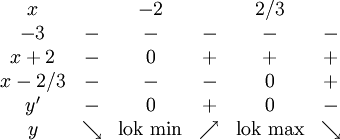
7.5.b)
En funktion $f(x)=g(x)^2$ som är kvadraten på en annan funktion kan man derivera antingen genom att använda produktregeln eller genom att använda kedjeregeln. Det första sättet ger $f'(x)=g'(x)g(x)+g(x)g'(x)=2g'(x)g(x)$ och det andra $f'(x)=2g(x)\cdot g'(x)$ eftersom den inre derivatan är $g'(x)$. Med $g(x)=\sin x$ ger detta $f'(x)=2\sin x\cos x=\sin 2x$. Lösningarna till ekvationen $\sin 2x=0$ är $2x=n\pi$, dvs $x=n\pi/2$, där $n=0,±1,±2,\ldots$. Teckenväxlingen är $-0+$ när $n$ är jämnt och $+0-$ då $n$ är udda. För $n=2m$, dvs $x=m\pi$, har vi således lokala minima och för $n=2m+1$, dvs $x=\pi/2+m\pi$, har vi lokala maxima.
7.5.d)
Derivatan är $y'=(e^x-e^{-x})/2$ som har ett enda nollställe $x=0$. Teckenväxligen är $-0+$, varför detta är ett lokalt minimum.
7.7.a)
Vi börjar med att undersöka funktionens nollställen och tecken (sådan information är alltid användbar när man skall rita grafer). Vi har förstås $y=0$ för $x=0$ och $x=-1$. Eftersom $y=x(x+1)$ så får vi teckenschemat

Vi har $y=x^2+x=x^2(1+1/x)$, vilket visar att $y\to\infty$ då
$x\to±\infty$. Derivatan är $y'=2x+1$ som är 0 för $x=-1/2$.
Teckenväxlingen är $-0+$, så funktionen har ett lokalt minimum där.
Inga asymptoter finns.
Anmärkning: Ett annat sätt är förstås att kvadratkomplettera, vilket
ger
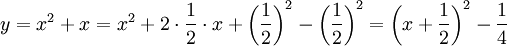
Här ser vi direkt att $y$ har ett lokalt minimum för $x=-1/2$ och
värdet är $-1/4$.
7.7.c)
Lägg först märke till att funktionen inte är definierad för $x=-2$. Vi har $y\to 0$ då $x\to\infty$, så $x$-axeln är en vågrät asymptot. Vidare gäller $y\to±\infty$ då $x\to -2_{±}$, så linjen $x=-2$ är en lodrät asymptot. Derivatan är $y'=-1/(x+2)^2$, som är $<0$ för $x\not=0$. Några lokala extremvärden finns alltså inte. Funktionen har inga nollställen och vi har $y<0$ för $x<-2$ och $y>0$ för $x>-2$.
7.7.d)
Funktionen har ett enda nollställe $x=0$. Nämnaren är 0 för $x=1$ och där är funktionen således inte definierad. Vi har $x^3-1=(x-1)(x^2+x+1)$, där polynomet $x^2+x+1=(x+1/2)^2+3/4$ är positivt för alla $x$. Alltså är $y<0$ då $x<1$ och $y>0$ då $x>1$. Omskrivningen
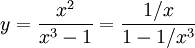
visar att $y\to 0$ då $x\to±\infty$, varför $x$-axeln är en vågrät asymptot.
Linjen $x=1$ är en lodrät asymptot eftersom $y\to±\infty$ då $x\to
1_{±}$. Vi deriverar:
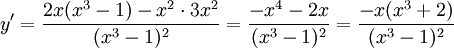
Derivatans nollställen är alltså 0 och $-\root3\of 2$.
Nämnaren är $\ge 0$ för alla $x$, så den behöver vi inte ta med i
teckenschemat:
![\begin{array}{cccccc} x & & - \sqrt[3]{2} & & 0 &\\ -1 & - & - & - & - & - \\ x & - & - & - & 0 & + \\ x^3+2 & - & 0 & + & + & + \\ y' & - & 0 & + & 0 & - \\ y &\searrow &\mbox{lok min} & \searrow & \mbox{lok max} &\searrow \end{array}](/wikis/mm1001_0701/images/math/5/4/3/54307f9902850df2c7ca5b8232998cbe.png)
Eventuellt kan man ta med punkten $x=1$ i teckenschemat, som en
påminnelse om att funktionen inte är definierad där.
7.7.f)
Funktionen är inte definierad för $x=1$ och har ett enda nollställe $x=4/3$. Teckenschema för funktionen:
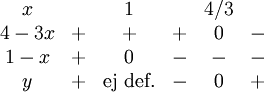
Vi har $y\to\infty$ då $x\to 1_{-}$ och $y\to-\infty$ då $x\to
1_{+}$, så linjen $x=1$ är en lodrät asymptot. Förkortar vi uttrycket
för $y$ med $x$ så får vi
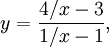
som går mot $(-3)/(-1)=3$ då $x\to±\infty$. Linjen $y=3$ är således en
vågrät asymptot. Derivatan är
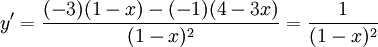
som saknar nollställen. Funktionen har därför inga lokala
extremvärden.
Anmärkning: Man kan se allt det här även genom att göra
en liten omskrivning: 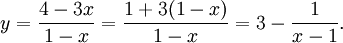 Grafen till $y=1/(x-1)$ får man genom att skjuta grafen till $y=1/x$
ett steg åt höger och grafen till $y=-1/(x-1)$ får man sedan genom att
spegla i $y$-axeln. Grafen till $y=3-1(x-1)$ får man till sist genom
att förskjuta 3 steg uppåt längs $y$-axeln.
Grafen till $y=1/(x-1)$ får man genom att skjuta grafen till $y=1/x$
ett steg åt höger och grafen till $y=-1/(x-1)$ får man sedan genom att
spegla i $y$-axeln. Grafen till $y=3-1(x-1)$ får man till sist genom
att förskjuta 3 steg uppåt längs $y$-axeln.
7.7.g)
Eftersom $4-x^2=(2-x)(2+x)$ så är funktionen inte definierad för $x=±2$. Den har ett enda nollställe för $x=5/2$. Vi börjar med att göra ett teckenschema för $y=-(2x-5)/(x+2)(x-2)$:
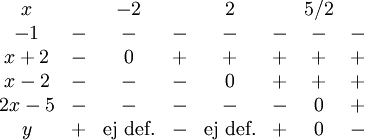
Eftersom täljaren har lägre grad än nämnaren, så gäller $y\to 0$ då
$x\to±\infty$. Alltså är $x$-axeln en vågrät asymptot. Lodräta
asymptoter är linjerna $x=±2$ eftersom $y\to\infty$ då $x\to -2_{-}$
och då $x\to 2_{+}$ och $y\to -\infty$ då $x\to -2_{+}$ och då $x\to 2_{-}$.
Derivatan är
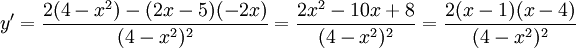
som har nollställena $x=1$ och $x=4$. Nämnaren är $\ge 0$ för alla $x$
och man behöver därför inte ta med den i teckenschemat, men man måste
ha i minnet att varken funktionen eller derivatan är definierad för
$x=±2$.