Lösningar 16
Matematik för naturvetare 15hp
| Versionen från 2 oktober 2007 kl. 13.34 (redigera) Clas Löfwall (Diskussion | bidrag) (Ny sida: ==Lösningar till några övningar till lektion 16== Tillbaka till lösningarna) ← Gå till föregående ändring |
Versionen från 16 oktober 2007 kl. 13.59 (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) Gå till nästa ändring → |
||
| Rad 2: | Rad 2: | ||
| [[Exempellösningar|Tillbaka till lösningarna]] | [[Exempellösningar|Tillbaka till lösningarna]] | ||
| + | |||
| + | |||
| + | ETT RÅD: Du kan alltid kontrollera svaret genom att derivera. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.1.e)''' | ||
| + | |||
| + | Observera att $\sqrt x=x^{1/2}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.1.f)''' | ||
| + | |||
| + | Skriv $3/x^3=3x^{-3}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.1.g)''' | ||
| + | |||
| + | Multiplicera först ihop. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.1.i)''' | ||
| + | |||
| + | Skriv $2/e^x=2e^{-x}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.e)''' | ||
| + | |||
| + | Börja med att utveckla kvadraten. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.f)''' | ||
| + | |||
| + | Gå över till den naturliga exponentialfunktionen: | ||
| + | $2^x=(e^{\ln 2})^x=e^{x\ln 2}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.g)''' | ||
| + | |||
| + | $(1+e^{-2x})e^{2x}=e^{2x}+1$ | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.h)''' | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int(2-3x)^{-3}\, dx&=&\left\{\begin{array}{ccc} | ||
| + | t&=&2-3x\\ | ||
| + | x&=&(2-t)/3\\ | ||
| + | dx&=&-dt/3\end{array}\right\}= | ||
| + | -\frac{1}{3}\int t^{-3}\, dt\\ | ||
| + | &=& \frac{1}{6t^2}+C=\frac{1}{6(2-3x)^2}+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.i)''' | ||
| + | |||
| + | Man kan först förenkla något: | ||
| + | |||
| + | <math> | ||
| + | \sin\left(\frac{¹x}{4}-\frac{¹}{2}\right)= | ||
| + | -\sin\left(\frac{¹}{2}-\frac{¹x}{4}\right)= | ||
| + | -\cos\frac{¹x}{4}</math> | ||
| + | |||
| + | De primitiva funktionerna är således | ||
| + | |||
| + | <math> | ||
| + | -\frac{4\sin(\pi x/4)}{\pi}+C.</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.j)''' | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\frac{1}{1-3x}\, dx&=&\left\{\begin{array}{ccc} | ||
| + | t&=&1-3x\\ | ||
| + | x&=&(1-t)/3\\ | ||
| + | dx&=&-dt/3\end{array}\right\}= | ||
| + | -\frac{1}{3}\int | ||
| + | \frac{dt}{t}\\ | ||
| + | &=&-\frac{1}{3}\ln|t|+C=-\frac{\ln|1-3x|}{3}+C\end{array} | ||
| + | |||
| + | |||
| + | |||
| + | '''9.2.k)''' | ||
| + | |||
| + | Funktionen är lika med $1/(2x^2+1)$. | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\frac{dx}{1+2x^2}&=&\left\{\begin{array}{ccc} | ||
| + | t&=&\sqrt 2\, x\\ | ||
| + | dt&=&\frac{1}{\sqrt 2}\, dx\end{array}\right\}= | ||
| + | \frac{1}{\sqrt 2}int\frac{dt}{1+t^2}\\ | ||
| + | &=&\frac{1}{\sqrt 2}\arctan t+C=\frac{1}{\sqrt 2}\arctan(\sqrt 2\, x)+C\end{array} | ||
| + | |||
| + | |||
| + | |||
| + | '''9.3.a)''' | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int e^{2x}(2x-5)^2\, dx&=&\left\{\begin{array}{ccc} | ||
| + | 2x-5&=&t\\ | ||
| + | 2\, dx&=& dt\\ | ||
| + | dx&=& dt/2\end{array}\right\}= | ||
| + | \int e^{t+5}t^2\, dt/2\\ | ||
| + | &=& | ||
| + | (e^5/2)\int t^2e^t\, dt=(e^5/2)t^2e^t-(e^5/2)\int 2te^t\, dt\\ | ||
| + | &=& | ||
| + | (e^5/2)t^2e^t-e^5te^t+e^5\int e^t\, dt \\ | ||
| + | &=& | ||
| + | (e^5/2)t^2e^t-e^5te^t+e^5+e^t+C\\ | ||
| + | &=& | ||
| + | e^5(2x-5)^2e^{2x-t}/2-e^5(2x-5)e^{2x-5}+e^5e^{2x-5}+C\\ | ||
| + | &=& | ||
| + | (2x-5)^2e^{2x}/2-(2x-5)e^{2x}+e^{2x}+C\\ | ||
| + | &=& | ||
| + | 2x^2e^{2x}-12xe^{2x}-(37/2)e^{2x}+C\end{array} | ||
| + | |||
| + | |||
| + | |||
| + | '''9.3.b)''' | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int (3x^3-5)\ln x\, dx&=&(3x^4/4-5x)\ln x-\int (3x^4/4-5x)(1/x)\, | ||
| + | dx\\ | ||
| + | &=& | ||
| + | (3x^4/4-5x)\ln x-\int(3x^3/4-5)\, dx\\ &=& | ||
| + | (3x^4/4-5x)\ln x-3x^4/16+5x+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''9.3.c)''' | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\ln(x-1)\, dx&=&(x-1)\ln(x-1)-\int (x-1)\cdot\frac{1}{x-1}\, dx\\ | ||
| + | &=& | ||
| + | (x-1)\ln(x-1)-\int 1\, dx=(x-1)\ln(x-1)-x+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''9.3.d)''' | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int e^{-x}\cos x\, dx&=&-e^{-x}\cos x-\int(-e^{-x})(\sin x)\, dx\\ | ||
| + | &=& | ||
| + | -e^{-x}\cos x-\int e^{-x}\sin x\, dx\\ | ||
| + | &=& | ||
| + | -e^{-x}\cos x+e^{-x}\sin x-\int e^{-x}\cos x\, dx+C\end{array}</math> | ||
| + | |||
| + | |||
| + | Alltså är | ||
| + | |||
| + | <math> | ||
| + | 2\int e^{-x}\cos x\, dx=-e^{-x}\cos x+e^{-x}\sin x+C=e^{-x}(\sin | ||
| + | x-\cos x)+C\] | ||
| + | och \[ | ||
| + | \int e^{-x}\cos x\, dx=\frac{1}{2}e^{-x}(\sin | ||
| + | x-\cos x)+C'</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''9.3.e)''' | ||
| + | |||
| + | Använd sambandet $\cos^2x=(1+\cos 2x)/2$: | ||
| + | |||
| + | <math> | ||
| + | \int e^{2x}\cos^2x\, dx= | ||
| + | \frac{1}{2}\int e^{2x}(1+\cos 2x)\, dx= | ||
| + | \frac{1}{4}e^{2x}+\frac{1}{2}\int e^{2x}\cos 2x\, dx</math> | ||
| + | |||
| + | Som en liten finess kan vi använda d) för att beräkna integralen: | ||
| + | |||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int e^{2x}\cos 2x\, dx&=&\left\{\begin{array}{ccccc} | ||
| + | 2x&=&-t\\ | ||
| + | x&=&-t/2\\ | ||
| + | dx&=&-dt/2\end{array}\right\}= | ||
| + | -\frac{1}{2}\int e^{-t}\cos(-t)\, dt\\ | ||
| + | &=& | ||
| + | -\frac{1}{2}\int e^{-t}\cos t\, dt= | ||
| + | -\frac{1}{2}\cdot \left(\frac{1}{2}e^{-t}(\sin t-\cos t)\right)+C\\ | ||
| + | &=& | ||
| + | -\frac{1}{4}e^{-t}(\sin t-\cos t)+C\\ | ||
| + | &=& | ||
| + | -\frac{1}{4}e^{2x}(\sin(-2x)-\cos(-2t))+C\\ | ||
| + | &=& | ||
| + | \frac{1}{4}e^{2x}(\sin 2x+\cos 2t)+C | ||
| + | \end{array}</math> | ||
| + | |||
| + | Svaret är således <math>\begin{array}{lll} | ||
| + | \int e^{2x}\cos^2x\, dx&=&\frac{1}{4}e^{2x}+\frac{1}{2}\cdot | ||
| + | \frac{1}{4}e^{2x}(\sin 2x+\cos 2t)+C\\ | ||
| + | &=& | ||
| + | \frac{1}{8}e^{2x}(2+\sin 2x+\cos 2x)+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | f) Om vi sätter $f(x)=\ln x$, så är integranden $f'(x)f(x)$, vilket | ||
| + | enligt kedjeregeln | ||
| + | är derivatan av $(f(x))^2/2$. Svaret är således $(\ln x)^2/2+C$. | ||
| + | |||
| + | |||
| + | |||
| + | g) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\ln(x^2+1)\, dx&=& | ||
| + | x\ln(x^2+1)-\int x\cdot \frac{2x}{x^2+1}\, dx\\ | ||
| + | &=& | ||
| + | x\ln(x^2+1)-2\int\left(1-\frac{1}{x^2+1}\right)\, dx\\ | ||
| + | &=& | ||
| + | x\ln(x^2+1)-2(x-\arctan x)+C\\ | ||
| + | &=& | ||
| + | x\ln(x^2+1)+2\arctan x-2x+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | 9.4.f) | ||
| + | |||
| + | <math> | ||
| + | \int\sin 2x\cos 2x\, dx=\frac{1}{2}\int\sin 4x\, dx=-\frac{1}{8}\cos | ||
| + | 4x+C</math> | ||
| + | |||
| + | |||
| + | |||
| + | h) | ||
| + | |||
| + | <math> | ||
| + | \int\frac{1}{8+2x^2}\, dx=\frac{1}{8}\int\frac{1}{1+(x/2)^2}\, dx= | ||
| + | \frac{1}{8}\cdot | ||
| + | 2\arctan\frac{x}{2}+C=\frac{1}{4}\arctan\frac{x}{2}+C</math> | ||
| + | |||
| + | |||
| + | |||
| + | i) | ||
| + | |||
| + | <math> | ||
| + | \int\frac{1}{x^2-4x+5}\, dx=\int\frac{1}{1+(x-2)^2}\, dx= | ||
| + | \arctan (x-2)+C</math> | ||
| + | |||
| + | |||
| + | |||
| + | j) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\frac{\sqrt{4-2x^2}}{x^2-2}\, dx&=& | ||
| + | -\sqrt | ||
| + | 2\int\frac{\sqrt{2-x^2}}{2-x^2}\, dx | ||
| + | = | ||
| + | -\sqrt 2\int\frac{1}{\sqrt{2-x^2}}\, dx\\&=& | ||
| + | -\int\frac{1}{\sqrt{1-(x/\sqrt 2)^2}}\, dx | ||
| + | = | ||
| + | -\sqrt 2\arcsin\frac{x}{\sqrt 2}+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | k) | ||
| + | |||
| + | <math> | ||
| + | \int\frac{1}{1-\cos x}\, dx=\int\frac{1}{2\sin^2(x/2)}\, dx= | ||
| + | -\frac{1}{2}\cdot 2\, \frac{1}{\tan(x/2)}+C= | ||
| + | -\frac{1}{\tan(x/2)}+C</math> | ||
| + | |||
| + | |||
| + | |||
| + | l) Använd trigonometriska ettan. | ||
| + | |||
| + | |||
| + | |||
| + | 9.5.a) Använder vi Exempel 9.26 så får vi | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\sqrt{4-x^2}\, dx&=&2\int\sqrt{1-(x/2)^2}\, | ||
| + | dx=\left\{\begin{array}{ccccc} | ||
| + | x/2&=&t\\ | ||
| + | dx&=&2\, dt\end{array}\right\}\\ | ||
| + | &=& | ||
| + | 4\int\sqrt{1-t^2}\, dt=4\left(\frac{1}{2}\arcsin | ||
| + | t+\frac{t}{2}\sqrt{1-t^2}\right)+C\\ | ||
| + | &=& | ||
| + | 2\arcsin\frac{x}{2}+x\sqrt{1-\frac{x^2}{4}}+C.\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | b) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\sqrt{1-\cos x}\, dx&=& | ||
| + | \int\sqrt{2\sin^2(x/2)}\, dx= | ||
| + | \sqrt 2 \int\sin(x/2)\, dx\\ | ||
| + | &=& | ||
| + | -2\sqrt 2\cos(x/2)+C\end{array}</math> | ||
| + | |||
| + | Observera att $\sin(x/2)\ge 0$ då $x\in\left[0,2¹\right]$, så att | ||
| + | |||
| + | <math> | ||
| + | \sqrt{\sin^2(x/2)}=|\sin(x/2)|=\sin(x/2).</math> | ||
| + | |||
| + | |||
| + | |||
| + | c) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\frac{x(x+1)}{x^2+1}\, dx&=&\int\frac{x^2+1+x-1}{x^2+1}\, dx\\ | ||
| + | &=& | ||
| + | \int\left(1+\frac{x}{x^2+1}-\frac{1}{x^2+1}\right)\, dx\\ | ||
| + | &=& | ||
| + | x+\frac{1}{2}\, \ln(x^2+1)-\arctan x+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | d) Integranden är $f(x)f'(x)$, där $f(x)=\arctan x$, som är | ||
| + | derivatan av $(f(x))^2/2$. Svaret är således $(\arctan x)^2/2+C$. | ||
| + | |||
| + | |||
| + | |||
| + | e) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\cos x\ln|\sin x|\, dx&=&\left\{\begin{array}{cccccc} | ||
| + | \sin x&=&t\\ | ||
| + | \cos x\, dx&=&dt\end{array}\right\} | ||
| + | =\int\ln|t|\, dt\\ | ||
| + | &=& | ||
| + | t\ln |t|-t+C=\sin x\ln|\sin x|-\sin x+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | f) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\cos x\cos 2x\, dx&=& | ||
| + | \int\cos x(1-2\sin^2x)\, dx=\left\{\begin{array}{ccccc} | ||
| + | t&=&\sin x\\ | ||
| + | dt&=&\cos x\, dx\end{array}\right\}\\ | ||
| + | &=& | ||
| + | \int(1-2t^2)\, dt=t-\frac{2t^3}{3}+C\\ | ||
| + | &=& | ||
| + | \sin x-\frac{2\sin^2x}{3}+C\end{array}</math> | ||
| + | |||
| + | Ett annat sätt är att använda additionsformeln för cosinus: | ||
| + | |||
| + | <math> | ||
| + | \cos (u+v)+\cos (u-v)=2\cos u\cos v,</math> | ||
| + | |||
| + | som ger | ||
| + | |||
| + | <math> | ||
| + | \cos x\cos 2x=\frac{1}{2}(\cos 3x+\cos x)</math> | ||
| + | |||
| + | |||
| + | och alltså | ||
| + | |||
| + | <math> | ||
| + | \int\cos x\cos 3x\, dx=\frac{\sin 3x}{6}+\frac{\sin x}{2}+C.</math> | ||
| + | |||
| + | |||
| + | Verifiera gärna att de två svaren är lika. | ||
| + | |||
| + | |||
| + | |||
| + | g) Eftersom $1+\tan^2x=1/\cos^2x$, så är | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\sin x\ln\left(\frac{2}{1+\tan^2x}\right)\, dx&=& | ||
| + | \int\sin x\ln (2\cos^2x)\, dx\\ | ||
| + | &=& | ||
| + | (\ln 2)\int\sin x\, dx+2\int\sin x\ln\cos x\, dx\end{array}</math> | ||
| + | |||
| + | |||
| + | Den första integralen är $-(\ln 2)\cos x+C$ och den andra | ||
| + | |||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\sin x\ln (2\cos^2x)\, dx&=&\left\{\begin{array}{cccc} | ||
| + | \cos x&=&t\\ | ||
| + | \sin x\, dx&=&-dt\end{array}\right\}= | ||
| + | -\int\ln t\, dt\\ | ||
| + | &=& | ||
| + | -(t\ln t-t)+C= | ||
| + | -\cos x\ln\cos x+\cos x+C\end{array}</math> | ||
| + | |||
| + | |||
| + | Svaret är således | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | &&-(\ln 2)\cos x+2(-\cos x\ln\cos x+\cos x)+C\\ | ||
| + | &=& | ||
| + | \cos x(2-\ln 2-2\ln \cos x)+C= | ||
| + | \cos x(2-\ln(2\cos^2 x))+C.\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | h) Sätt $t=x^2$. | ||
| + | |||
| + | |||
| + | |||
| + | i) Sätt $t=x^3$. | ||
| + | |||
| + | |||
| + | |||
| + | 9.6.c) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int\frac{x^3}{\sqrt{1-x^4}}\, dx&=& | ||
| + | \left\{\begin{array}{ccccc} | ||
| + | x^4&=&t\\ | ||
| + | x^3\, dx&=&dt/4\end{array}\right\}= | ||
| + | \frac{1}{4}\int\frac{1}{\sqrt{1-t}}\, dt\\ | ||
| + | &=& | ||
| + | \frac{1}{4}\int(1-t)^{-1/2}\, dt= | ||
| + | -\frac{1}{2}(1-t)^{1/2}+C | ||
| + | =-\frac{\sqrt{1-x^4}}{2}+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | d) Sätt $t=\cos x$. | ||
| + | |||
| + | |||
| + | |||
| + | e) Partialintegrera två gånger: | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int e^{2x}\cos 3x\, dx&=&\frac{1}{2}e^{2x}\cos | ||
| + | 3x+\frac{3}{2}\int e^{2x}\sin 3x\, dx\\ | ||
| + | &=& | ||
| + | \frac{1}{2}e^{2x}\cos 3x+\frac{3}{4}e^{2x}\sin 3x- | ||
| + | \frac{9}{4}\int e^{2x}\cos 3x\, dx\end{array}</math> | ||
| + | |||
| + | |||
| + | (Lägg märke till att de primitiva funktionerna i första och sista | ||
| + | ledet inte behöver vara lika.) | ||
| + | Löser man ut $\int e^{2x}\cos 3x\, dx$ så får man | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int e^{2x}\cos 3x\, dx&=&-\frac{4}{13}\left( | ||
| + | \frac{1}{2}e^{2x}\cos 3x+\frac{3}{4}e^{2x}\sin 3x\right)\\ | ||
| + | &=& | ||
| + | -\frac{1}{13}e^{2x}\left(2\cos 3x+3\sin 3x\right)+C.\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | f) | ||
| + | |||
| + | <math>\begin{array}{lll} | ||
| + | \int x\arctan \frac{1}{x}\, dx&=& | ||
| + | \frac{x^2}{2}\arctan\frac{1}{x}-\int\frac{x^2}{2}\left(-\frac{1}{x^2}\right) | ||
| + | \frac{1}{1+1/x^2}\, dx\\ | ||
| + | &=& | ||
| + | \frac{x^2}{2}\arctan\frac{1}{x}+\frac{1}{2}\int\frac{x^2}{1+x^2}\, | ||
| + | dx\\ | ||
| + | &=& | ||
| + | \frac{x^2}{2}\arctan\frac{1}{x}+\frac{1}{2}\int\left(1-\frac{1}{1+x^2}\right)\, dx\\ | ||
| + | &=& | ||
| + | \frac{x^2}{2}\arctan\frac{1}{x}+\frac{1}{2}(x-\arctan | ||
| + | x)+C\end{array}</math> | ||
| + | |||
| + | |||
| + | |||
| + | 9.8. I intervallet $0\le t\le 5$ är $V'(t)\ge 0$, så den maximala | ||
| + | volymen fås för $t=5$. Vi har | ||
| + | |||
| + | <math> | ||
| + | V(t)=\frac{1}{20}\left(\frac{5t^3}{3}-\frac{t^4}{4}\right)+C</math> | ||
| + | |||
| + | |||
| + | och eftersom $V(0)=0,5$ så måste $C=0,5$. Den maximala volymen är | ||
| + | således | ||
| + | |||
| + | <math> | ||
| + | V(5)=\frac{1}{20}\left(\frac{5\cdot 5^3}{3}-\frac{5^4}{4}\right)+ | ||
| + | 0,5=\frac{149}{48}\approx 3\quad\mbox{liter}.</math> | ||
| + | |||
| + | |||
| + | |||
| + | 9.9. Vi studerar först derivatans nollställen och teckenväxlingarna. | ||
| + | Vi har $P_{d}'(t)=0\Leftrightarrow 1664-144t-t^3=0$. För att hitta | ||
| + | rötterna till tredjegradsekvationen gissar vi heltalsrötter. En | ||
| + | heltalsrot måste dela 1664 och man hittar roten $t=8$. Då är $t-8$ en | ||
| + | faktor i $1664-144t-t^3$ och division ger | ||
| + | $1664-144t-t^3=(8-t)(t^2+8t+208)$. Den andra faktorn har inga | ||
| + | nollställen. Vi har alltså | ||
| + | |||
| + | <math> | ||
| + | P_{d}'(t)=\frac{(8-t)(t^2+8t+208)}{4(144+t^2)}</math> | ||
| + | |||
| + | |||
| + | och teckenväxlingen vid 8 är $+0-$, vilket visar att 8 är ett lokalt | ||
| + | maximum. Syrekoncentrationen är alltså störst 8 timmar efter gryningen. | ||
| + | |||
| + | |||
| + | |||
| + | Vi ska nu bestämma funktionen $P_{d}$. Division ger | ||
| + | |||
| + | <math> | ||
| + | P_{d}'(t)=\frac{416}{144+t^2}-\frac{t}{4}=\frac{26/9}{1+(t/12)^2} | ||
| + | -\frac{t}{4},</math> | ||
| + | |||
| + | |||
| + | vilket ger | ||
| + | |||
| + | <math> | ||
| + | P_{d}(t)=\frac{416}{144}\cdot 12\arctan\frac{t}{12}-\frac{t^2}{8}+C= | ||
| + | \frac{104}{3}\arctan\frac{t}{12}-\frac{t^2}{8}+C.</math> | ||
| + | |||
| + | |||
| + | Det minsta värdet av $P_{d}$ antas antingen för $t=0$ eller för | ||
| + | $t=12$ (eftersom det finns exakt ett lokalt maximum). Nu är | ||
| + | |||
| + | <math> | ||
| + | P_{d}(12)=\frac{26¹}{3}-18+C,</math> | ||
| + | |||
| + | |||
| + | vilket är $>P_{d}(0)=C$. Det minsta värdet är tydligen $C$, dvs | ||
| + | $C=13$. Då $0\le t\le 12$ är således | ||
| + | |||
| + | <math> | ||
| + | P_{d}(t)\frac{104}{3}\arctan\frac{t}{12}-\frac{t^2}{8}+13.</math> | ||
| + | |||
| + | |||
| + | För $12\le t\le 24$ avtar $P_{d}$ linjärt på så sätt att | ||
| + | $P_{d}(12)=26¹/3-5$ och $P_{d}(24)=P_{d}(0)=13$. Detta ger | ||
| + | |||
| + | <math> | ||
| + | P_{d}(t)-13=\frac{26¹/3-5-13}{12-24}(x-24)\quad\mbox{eller}\quad | ||
| + | P_{d}(t)=\frac{27-13¹}{18}t+\frac{26¹}{3}-23.</math> | ||
Versionen från 16 oktober 2007 kl. 13.59
Lösningar till några övningar till lektion 16
ETT RÅD: Du kan alltid kontrollera svaret genom att derivera.
9.1.e)
Observera att $\sqrt x=x^{1/2}$.
9.1.f)
Skriv $3/x^3=3x^{-3}$.
9.1.g)
Multiplicera först ihop.
9.1.i)
Skriv $2/e^x=2e^{-x}$.
9.2.e)
Börja med att utveckla kvadraten.
9.2.f)
Gå över till den naturliga exponentialfunktionen: $2^x=(e^{\ln 2})^x=e^{x\ln 2}$.
9.2.g)
$(1+e^{-2x})e^{2x}=e^{2x}+1$
9.2.h)
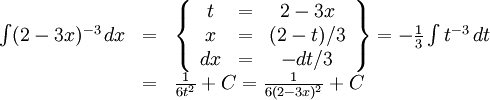
9.2.i)
Man kan först förenkla något:

De primitiva funktionerna är således
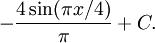
9.2.j)
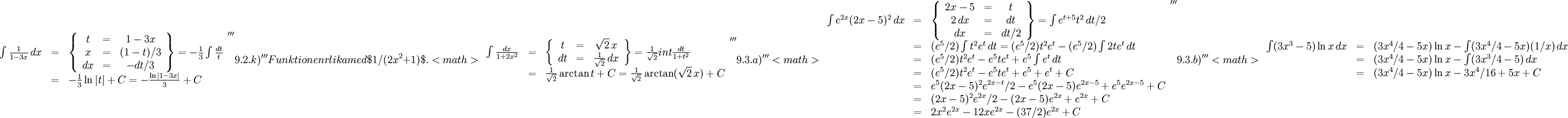
9.3.c)

9.3.d)
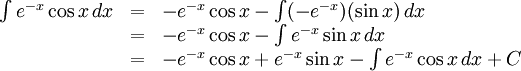
Alltså är
Misslyckades med att tolka formel. (okänt fel): 2\int e^{-x}\cos x\, dx=-e^{-x}\cos x+e^{-x}\sin x+C=e^{-x}(\sin x-\cos x)+C\] och \[ \int e^{-x}\cos x\, dx=\frac{1}{2}e^{-x}(\sin x-\cos x)+C'
9.3.e)
Använd sambandet $\cos^2x=(1+\cos 2x)/2$:

Som en liten finess kan vi använda d) för att beräkna integralen:

Svaret är således 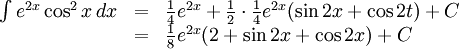
f) Om vi sätter $f(x)=\ln x$, så är integranden $f'(x)f(x)$, vilket enligt kedjeregeln är derivatan av $(f(x))^2/2$. Svaret är således $(\ln x)^2/2+C$.
g)
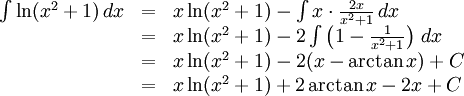
9.4.f)
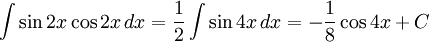
h)
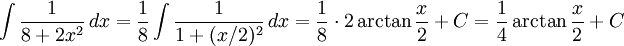
i)
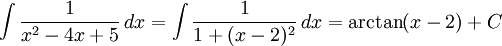
j)
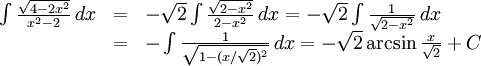
k)
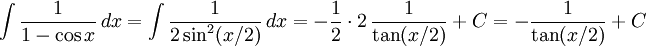
l) Använd trigonometriska ettan.
9.5.a) Använder vi Exempel 9.26 så får vi
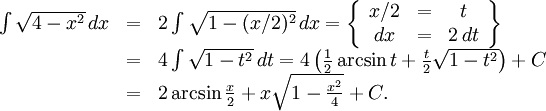
b)
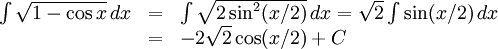
Observera att $\sin(x/2)\ge 0$ då $x\in\left[0,2¹\right]$, så att

c)
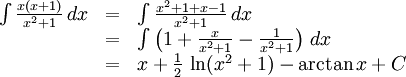
d) Integranden är $f(x)f'(x)$, där $f(x)=\arctan x$, som är derivatan av $(f(x))^2/2$. Svaret är således $(\arctan x)^2/2+C$.
e)
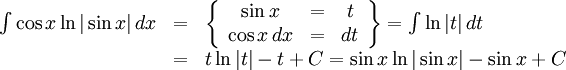
f)
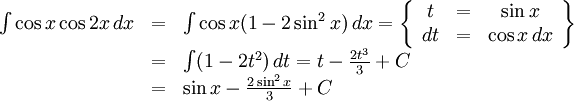
Ett annat sätt är att använda additionsformeln för cosinus:
cos(u + v) + cos(u − v) = 2cosucosv,
som ger
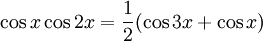
och alltså
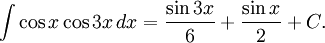
Verifiera gärna att de två svaren är lika.
g) Eftersom $1+\tan^2x=1/\cos^2x$, så är
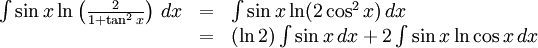
Den första integralen är $-(\ln 2)\cos x+C$ och den andra
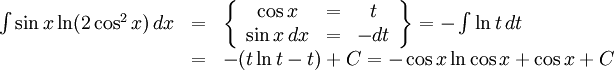
Svaret är således
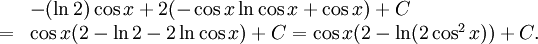
h) Sätt $t=x^2$.
i) Sätt $t=x^3$.
9.6.c)
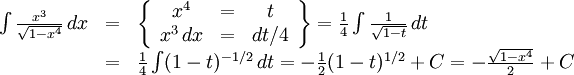
d) Sätt $t=\cos x$.
e) Partialintegrera två gånger:
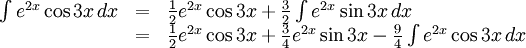
(Lägg märke till att de primitiva funktionerna i första och sista
ledet inte behöver vara lika.)
Löser man ut $\int e^{2x}\cos 3x\, dx$ så får man
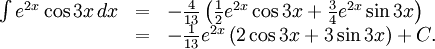
f)

9.8. I intervallet $0\le t\le 5$ är $V'(t)\ge 0$, så den maximala volymen fås för $t=5$. Vi har
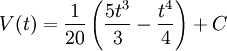
och eftersom $V(0)=0,5$ så måste $C=0,5$. Den maximala volymen är
således
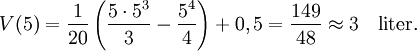
9.9. Vi studerar först derivatans nollställen och teckenväxlingarna. Vi har $P_{d}'(t)=0\Leftrightarrow 1664-144t-t^3=0$. För att hitta rötterna till tredjegradsekvationen gissar vi heltalsrötter. En heltalsrot måste dela 1664 och man hittar roten $t=8$. Då är $t-8$ en faktor i $1664-144t-t^3$ och division ger $1664-144t-t^3=(8-t)(t^2+8t+208)$. Den andra faktorn har inga nollställen. Vi har alltså
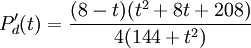
och teckenväxlingen vid 8 är $+0-$, vilket visar att 8 är ett lokalt
maximum. Syrekoncentrationen är alltså störst 8 timmar efter gryningen.
Vi ska nu bestämma funktionen $P_{d}$. Division ger
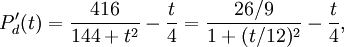
vilket ger
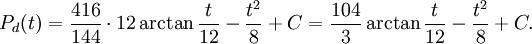
Det minsta värdet av $P_{d}$ antas antingen för $t=0$ eller för
$t=12$ (eftersom det finns exakt ett lokalt maximum). Nu är
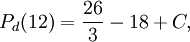
vilket är $>P_{d}(0)=C$. Det minsta värdet är tydligen $C$, dvs
$C=13$. Då $0\le t\le 12$ är således
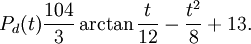
För $12\le t\le 24$ avtar $P_{d}$ linjärt på så sätt att
$P_{d}(12)=26¹/3-5$ och $P_{d}(24)=P_{d}(0)=13$. Detta ger


