Lektion 4
Matematik för naturvetare 15hp
| Versionen från 25 augusti 2007 kl. 08.55 (redigera) Clas Löfwall (Diskussion | bidrag) ← Gå till föregående ändring |
Nuvarande version (27 augusti 2007 kl. 14.49) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) |
||
| (En mellanliggande version visas inte.) | |||
| Rad 1: | Rad 1: | ||
| + | [[Läsanvisningar | Tillbaka till läsanvisningarna]] | ||
| + | |||
| ==Välkommen till Lektion 4!== | ==Välkommen till Lektion 4!== | ||
| Rad 14: | Rad 16: | ||
| '''Viktiga saker att tänka på när du läser''' | '''Viktiga saker att tänka på när du läser''' | ||
| + | '''Avsnitt 2.1''' | ||
| + | |||
| + | |||
| + | Definitionen av talföljd i boken är något kryptisk, men egentligen är | ||
| + | det något väldigt enkelt: en talföljd är helt enkelt en följd | ||
| + | av tal $a_{1},a_{2},a_{3},\ldots$. Talen $a_{n}$, som kallas | ||
| + | följdens ''element'', kan vara heltal, reella tal | ||
| + | eller komplexa tal och följden kan vara ändlig eller oändlig, även om | ||
| + | det senare är det vanligaste i matematiken. När man | ||
| + | allmänt diskuterar talföljder så brukar numreringen av elementen | ||
| + | $a_{n}$ börja på $n=1$, men det är inte nödvändigt; ibland kan det | ||
| + | vara ändamålsenligt att numrera dem på något annat sätt. Det finns | ||
| + | flera olika sätt att definiera elementen i en talföljd: | ||
| + | |||
| + | |||
| + | * Med hjälp av en formel som i Exempel 2.1 och 2.2. | ||
| + | |||
| + | |||
| + | *''Rekursivt'', vilket innebär att $a_{n}$ uttrycks med hjälp | ||
| + | av ett eller flera av de föregående elementen. Följderna i Exempel | ||
| + | 2.9, 2.10 och 2.11 är rekursivt definierade. | ||
| + | |||
| + | |||
| + | * Genom någon egenskap, t ex att kvoten mellan två på varandra | ||
| + | följande element alltid har samma värde (dvs en geometrisk talföljd, se | ||
| + | nedan och boken Exempel 2.5 samt avsnitt 2.2). | ||
| + | |||
| + | |||
| + | * På något annat, mer eller mindre fantasifullt sätt. Exempelvis | ||
| + | skulle man kunna låta $a_{n}$ vara antalet bokstäver i ord nummer $n$ | ||
| + | i ''Krig och fred''. Tolstojs roman är visserligen ganska tjock, men | ||
| + | följden blir förstås ändå ändlig. | ||
| + | |||
| + | |||
| + | |||
| + | Däremot kan man inte säga att en talföljd är given om man bara ger några termer, som t.ex. i Exempel 2.5. Vad punkterna står för kan man bara gissa. Det kan vara formeln som står i boken som bestämmer talföljden, dvs att nästa tal fås genom att multiplicera föregående tal med 3, men det skulle kunna vara något helt annat. En annan formel som stämmer är | ||
| + | |||
| + | |||
| + | <math>a_n=2+4(n-1)+4(n-1)(n-2)+8/3(n-1)(n-2)(n-3)</math> | ||
| + | |||
| + | |||
| + | (kontrollera gärna genom att stoppa in $n=1,2,3,4$) men då skulle det gälla att <math>a_5=130</math> och inte $3\cdot54=162$. I själva verket kan man för ett godtyckligt antal termer alltid hitta ett polynomuttryck av ovanstående typ, så att formeln stämmer för dessa termer. I övning 2.2 är alltså de svar som anges i facit bara förslag, det finns andra svar som är lika korrekta. | ||
| + | |||
| + | |||
| + | |||
| + | '''Avsnitt 2.2''' | ||
| + | |||
| + | |||
| + | Aritmetiska följder och summor är, till skillnad från geometriska, | ||
| + | inte så vanliga i tillämpningar. Sats 2.2 är därför betydligt | ||
| + | viktigare än Sats 2.1. Ett sätt att komma ihåg formeln i Sats 2.1 är att lära sig följande sätt att läsa formeln: | ||
| + | |||
| + | |||
| + | ''antalet termer gånger första plus sista genom två'' | ||
| + | |||
| + | |||
| + | Observera att de $n$ första talen i den geometriska talföljden $a, ak,ak^2,ak^3,\ldots,ak^n,\ldots$, som det står om i Sats 2.2, är $a, ak,ak^2,ak^3,\ldots,ak^{n-1}$. Den n:te termen är alltså $ak^{n-1}$ och inte $ak^{n}$. Formeln för summan i fallet $k\ne1$ kan skrivas | ||
| + | |||
| + | |||
| + | <math>\frac{k\cdot ak^{n-1}-a}{k-1} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | och därför kan man lära sig följande läsning av fomeln i Sats 2.2 | ||
| + | |||
| + | |||
| + | ''k gånger sista minus första genom k minus 1'' | ||
| + | |||
| + | |||
| + | Detta kan med fördel användas t.ex. när man skall lösa Testproblem 3 d). | ||
| + | |||
| + | |||
| + | Sist i Sats 2.1 och 2.2 står en mening som inte är så bra formulerad. I Sats 2.1 bör den lyda så här i stället: "Summan $S_n$ kallas en aritmetisk summa." | ||
| + | Och i Sats 2.2 bör den lyda så här: "Summan $S_n$ kallas en geometrisk summa." | ||
| + | |||
| + | |||
| + | Efter Exempel 2.17 införs det viktiga | ||
| + | begreppet ''serie''. En ''summa'' har alltid bara ändligt många | ||
| + | termer, medan en serie kan ha oändligt många. Eftersom man inte kan | ||
| + | lägga ihop oändligt många termer, så är det inte självklart vad man | ||
| + | skall mena med "summan av en serie". I kapitlet om gränsvärden kommer | ||
| + | detta att diskuteras. Att man måste vara aktsam när man manipulerar | ||
| + | serier framgår av följande halsbrytande räkning: | ||
| + | |||
| + | Betrakta talföljden | ||
| + | $a_{n}=(-1)^n$, $n=0,1,2,\ldots$ och motsvarande serie | ||
| + | $a_{0}+a_{1}+a_{2}+\ldots=1-1+1-1+1-1+\ldots$. Låt oss sätta in | ||
| + | parenteser på två olika sätt och försöka räkna ut summan: å ena sidan | ||
| + | är $$ | ||
| + | 1-1+1-1+1-1+\ldots =(1-1)+(1-1)+(1-1)+\ldots=0+0+0+\ldots =0$$ | ||
| + | och å den andra sidan är $$ | ||
| + | 1-1+1-1+1-1+\ldots =1-(1-1)-(1-1)-\ldots=1-0-0-\ldots =1$$ | ||
| + | |||
| + | Har vi funnit en motsägelse i matematiken? Nej, lösningen på den här | ||
| + | paradoxen är att ''man får inte manipulera serier på samma sätt som ändliga summor''. | ||
| + | |||
| + | |||
| + | |||
| + | '''Avsnitt 2.3''' | ||
| + | |||
| + | |||
| + | Summasymbolen $\sum$ känner du förmodligen till sedan tidigare, och om | ||
| + | inte, så är det bra om du lär dig använda den nu. Produkttecknet $\prod$ är ett stort pi. En | ||
| + | särskilt viktig produkt är ''fakulteten'' $n!$ som definieras på sid 71. | ||
| + | |||
| + | Således är $1!=1$ (då har produkten bara en enda faktor), $2!=1\cdot | ||
| + | 2=2$, $3!=1\cdot 2\cdot 3=6$ osv. Räkna ut $4!$, $5!$ och $6!$ själv. | ||
| + | Observera att för $n\ge 2$ gäller | ||
| + | |||
| + | $$ | ||
| + | n!=1\cdot 2\cdot 3\cdot\ldots \cdot (n-1)\cdot n=(n-1)!\cdot n$$ | ||
| + | |||
| + | |||
| + | Den här formeln kan man använda man för att motivera definitionen av $0!$ på sid 78. Om vi vill | ||
| + | att formeln skall gälla även då $n=1$, så måste | ||
| + | |||
| + | $$ | ||
| + | 1!=(1-1)!\cdot 1=0!$$ | ||
| + | |||
| + | och därför väljer man att definiera $0!$ som 1. | ||
| + | Jämför detta med hur man gör för att definiera $a^0$. | ||
| + | |||
| + | |||
| + | |||
| + | Fakulteter uppträder naturligt i många matematiska sammanhang, som du | ||
| + | kommer att se i kursen. En tillämpning är att $n!$ är antalet sätt man kan ordna $n$ element. T.ex. kan fem personer ordna upp sig i en kö på $5!=120$ sätt. En annan tillämpning finns på sid 222, som behandlar högre derivator: Låt $f(x)=(1+x)^n$, där $n$ är ett positivt heltal, dvs $n=1,2,3,\ldots$. | ||
| + | Deriverar vi $f$ upprepade gånger så får vi | ||
| + | |||
| + | |||
| + | <math>\displaystyle | ||
| + | f'(x)=n(1+x)^{n-1}</math> | ||
| + | |||
| + | <math>\displaystyle f''(x)=n(n-1)(1+x)^{n-2}</math> | ||
| + | |||
| + | <math>\displaystyle f^{(3)}(x)=n(n-1)(n-2)(1+x)^{n-3}</math> | ||
| + | |||
| + | <math>\displaystyle f^{(4)}(x)=n(n-1)(n-2)(n-3)(1+x)^{n-4}</math> | ||
| + | |||
| + | <math>\displaystyle f^{(5)}(x)=n(n-1)(n-2)(n-3)(n-4)(1+x)^{n-5}</math> | ||
| + | |||
| + | |||
| + | |||
| + | och allmänt | ||
| + | |||
| + | |||
| + | <math> | ||
| + | f^{(k)}(x)=n(n-1)\ldots (n-(k-1))(1+x)^{n-k}</math> | ||
| + | |||
| + | |||
| + | (beteckningen $f^{(k)}$ betyder alltså derivatan av ordning $k$ till | ||
| + | $f$). Derivatan av ordning $n$ blir således | ||
| + | |||
| + | |||
| + | <math> | ||
| + | f^{(n)}(x)=n(n-1)\ldots 2\cdot 1\cdot (1+x)^{n-n}=n!</math> | ||
| + | |||
| + | |||
| + | Även produkten $n(n-1)\ldots (n-(k-1))$ kan uttryckas med hjälp av | ||
| + | fakulteter: | ||
| + | |||
| + | |||
| + | <math> | ||
| + | n(n-1)\ldots (n-(k-1)) | ||
| + | =\frac{n(n-1)\ldots (n-(k-1))\cdot | ||
| + | (n-k)(n-k-1)\ldots 2\cdot 1}{(n-k)(n-k-1)\ldots 2\cdot 1} | ||
| + | =\frac{n!}{(n-k)!}</math> | ||
| + | |||
| + | |||
| + | Sammanfattningsvis är alltså | ||
| + | |||
| + | |||
| + | <math> | ||
| + | f^{(k)}(x)=\frac{n!}{(n-k)!}\, (1+x)^{n-k}</math> | ||
| + | |||
| + | |||
| + | |||
| + | '''Avsnitt 2.5''' | ||
| + | |||
| + | |||
| + | Ett ''binom'' är ett uttryck med två termer, t ex $a+b$. Enligt | ||
| + | kvadreringsregeln är | ||
| + | |||
| + | $$ | ||
| + | (a+b)^2=a^2+2ab+b^2$$ | ||
| + | |||
| + | och "kuberingsregeln" säger att | ||
| + | |||
| + | $$ | ||
| + | (a+b)^3=a^3+3a^2b+3ab^2+b^3$$ | ||
| + | |||
| + | |||
| + | Jämför detta med "första kubregeln" på sid 42 som säger att $a^3+b^3=(a+b)(a^2-ab+b^2)$ vilket är något helt annat än "kuberingsregeln". Det gäller alltså ''inte'' att $(a+b)^3=a^3+b^3$ (och inte heller att $(a+b)^2=a^2+b^2$). | ||
| + | |||
| + | Den viktiga ''binomialsatsen'', som formuleras i Sats 2.5 och längst ned på sid 81, är generaliseringen av de här | ||
| + | formlerna till högre potenser $(a+b)^n$. | ||
| + | |||
| + | Studera utvecklingarna på sid 76. Hur får man t.ex. den sista raden från raden ovanför? Jo, de fyra termerna i utvecklingen av $(a+b)^3$ skall alla multipliceras med dels $a$ och dels $b$. Hur uppstår då termer på formen $a^2b^2$? Jo, genom att antingen multiplicera termen $3a^2b$ med $b$ eller att multiplicera termen $3ab^2$ med $a$ (och summera). Alltså förstår vi att talet 6 framför $a^2b^2$ har uppkommit genom att summera de två treorna på raden ovanför. På samma sätt ser vi att fyran framför $a^3b$ (eller framför $ab^3$) uppstår genom att summera ettan och trean på raden ovanför. Ettan längst till vänster (eller höger) uppstår genom att föra ned ettan på raden ovanför (och om man så vill summera en osynlig nolla). | ||
| + | |||
| + | Man inser att detta är ett generellt sätt att resonera, så vi kan nu lätt hitta utvecklingen av $(a+b)^5$ genom att summera intilliggande tal i den sista raden. Då får vi koefficienterna 1, 5, 10, 10, 5, 1 (och vi har därmed genomfört uppmaningen i boken efter utvecklingarna). Utan att snegla på sid 77, så kan du försöka skriva upp raden av koefficienter i utvecklingen av $(a+b)^6$. | ||
| + | |||
| + | Boken inför nu beteckningen <math>\binom nk</math> som utläses "n över k" och kallas binomialkoefficienter och som alltså är en beteckning för koefficienten framför $a^{n-k}b^k$ i utvecklingen av $(a+b)^n$. Utvecklingen av $(a+b)^4$ kan alltså skrivas | ||
| + | |||
| + | |||
| + | <math>\binom 40 a^4+\binom 41 a^3b+\binom 42 a^2b^2+\binom 43 ab^3+\binom 44 b^4</math> | ||
| + | |||
| + | |||
| + | och allmänt gäller utvecklingen som står längst ned på sid 81, med eller utan användning av summa-symbolen. Eftersom första och sista koefficienten alltid är 1 och eftersom utvecklingen är symmetrisk (det blir samma om man läser från vänster eller höger), så har vi följande samband | ||
| + | |||
| + | |||
| + | <math>\binom n0=1\quad\binom nn=1\quad\binom nk=\binom n{n-k}</math> | ||
| + | |||
| + | |||
| + | Dessutom gäller den viktiga egenskapen <math>{\rm II.}</math> som står i rutan på sid 81. Det är den egenskapen som vi diskuterade oss fram till ovan och som bestämmer koefficienterna rad för rad. Om vi placerar binomialkoefficienterna i form av "Pascals triangel" som på sid 77, så kan alltså denna egenskap utläsas som | ||
| + | |||
| + | |||
| + | ''en binomialkoefficient är summan av dess två grannar på raden ovanför i Pascals traingel'' | ||
| + | |||
| + | |||
| + | Binomialkoefficienten <math>\binom nk</math> kan också ges en kombinatorisk tolkning. Den utgör antalet sätt att välja $k$ element ur $n$ element (utan att ta hänsyn till ordningen mellan elementen). Till exempel finns det <math>\binom 63=20</math> sätt att bland sex personer välja en kommitté bestående av tre personer (utan inbördes rangordning). Om en provfråga har fem svarsalternativ och man vet att precis två är rätt, så behövs maximalt <math>\binom 52=10</math> försök innan man fått rätt svar. Det är inte så konstigt att binomialkoefficienterna har denna tolkning, eftersom utvecklingen av $(a+b)^n$ fås genom att multiplicera ihop $n$ st parenteser $(a+b)$ och detta sker genom att ur varje parentes välja antingen $a$ eller $b$ (och multiplicera). Antalet termer på formen $a^{n-k}b^{k}$ är därför antalet sätt att välja ut $k$ parenteser ur $n$ (de parenteser där man väljer $b$). | ||
| + | |||
| + | Nu kan vi det mesta man behöver veta om binomialsatsen och binomialkoefficienterna, men det finns ytterligare en nyttig sak att lära sig, nämligen en explicit formel för binomialkoefficienterna. För att i praktiken räkna ut binomialkoefficienter så duger Pascals triangel utmärkt, men i vissa teoretiska ssammanhang så ger en formel mer information. Formeln som jag tänker på hittar du överst på sid 78. Genom att förkorta med $(n-k)!$ kan formeln också skrivas | ||
| + | |||
| + | |||
| + | <math>\binom nk=\frac{n(n-1)(n-2)\cdots(n-k+1)}{k!}</math> | ||
| + | |||
| + | |||
| + | Ett sätt att kombinatoriskt resonera sig fram till att denna formel uttrycker antalet sätt att välja $k$ parenteser bland $n$ parenteser är följande (=överkurs). | ||
| + | |||
| + | Den första parentesen kan väljas på $n$ sätt. Oberoende av det valet kan vi välja nästa parentes på $n-1$ sätt, dvs de två första parenteserna kan väljas på $n(n-1)$ sätt. Fortsätter man på detta sätt finner man att man kan välja $k$ parenteser i ordning bland $n$ parenteser på $n(n-1)(n-2)\cdots(n-k+1)$ sätt. Men vi är inte intresserade av vilken ordning vi väljer parenteserna. Det går att ordna $k$ parenteser på $k!$ sätt (se ovan). Alltså kommer varje val av $k$ parenteser att räknas $k!$ gånger, vilket motiverar att vi skall dividera med $k!$ för att få svaret. | ||
| + | |||
| + | Bokens bevis går ut på följande (också överkurs). Inför beteckningen <math>{\rm binom}(n,k)=\frac{n!}{k!(n-k)!}</math>. Vi vill alltså visa att <math>\binom nk={\rm binom}(n,k)</math>. Genom att stoppa in $k=0$ och $k=n$ i formeln (och utnyttja definitionen $0!=1$) så får vi att | ||
| + | ${\rm binom}(n,0)={\rm binom}(n,n)=1$. Lemma 2.1 säger att ${\rm binom}(n+1,k)={\rm binom}(n,k)+{\rm binom}(n,k-1)$. Detta betyder att ${\rm binom}(n,k)$ kan beräknas successivt på samma sätt som <math>\binom nk</math> via Pascals triangel och de måste därför vara lika. | ||
| + | |||
| + | |||
| + | Låt oss till slut föregripa lite om "Maclaurinserier" (se sid 220) och kombinera resultatet ovan om de högre derivatorna av funktionen $f(x)=(1+x)^n$ med binomialsatsen. Enligt ovan har vi att | ||
| + | |||
| + | |||
| + | |||
| + | <math>f^{(k)}(x)=\frac{n!}{(n-k)!}\,(1+x)^{n-k}</math> | ||
| + | |||
| + | |||
| + | för $k\le n$ och $\displaystyle f^{(k)}(x)=0$ för $k>n$. Alltså gäller | ||
| + | |||
| + | |||
| + | <math>f^{(k)}(0)=\frac{n!}{(n-k)!}</math> | ||
| + | |||
| + | |||
| + | för $k\le n$ och $\displaystyle f^{(k)}(0)=0$ för $k>n$ vilket ger att | ||
| + | |||
| + | |||
| + | <math>\frac{f^{(k)}(0)}{k!}=\frac{n!}{k!(n-k)!}=\binom nk</math> | ||
| + | |||
| + | |||
| + | för $k\le n$ och | ||
| + | |||
| + | |||
| + | <math>\frac{f^{(k)}(0)}{k!}=0</math> | ||
| + | |||
| + | |||
| + | för $k>n$. Maclaurinserien för funktionen $f$ är därför | ||
| + | |||
| + | |||
| + | <math>f(x)=\sum_{k=0}^\infty \frac{f^{(k)}(0)}{k!} x^k=\sum_{k=0}^n \binom nk x^k</math> | ||
| + | |||
| + | |||
| + | medan binomialsatsen tillämpad på $f(x)=(1+x)^n$ ger | ||
| + | |||
| + | |||
| + | <math>f(x)=\sum_{k=0}^n \binom nk x^k</math> | ||
| + | |||
| + | |||
| + | Vi får alltså samma resultat, vilket ju känns tryggt. | ||
Nuvarande version
Tillbaka till läsanvisningarna
[redigera] Välkommen till Lektion 4!
I den här lektionen ska vi titta närmare på talföljder och serier. Vi ska även lära oss ett viktigt matematiskt resultat som kallas för Binomialsatsen.
Du ska studera följande kapitel i boken:
- 2.1 Följder av tal
- 2.2 Summor och serier
- 2.3 Symboler för summa och produkt
- 2.5 Binomialsatsen (ej bevis)
Viktiga saker att tänka på när du läser
Avsnitt 2.1
Definitionen av talföljd i boken är något kryptisk, men egentligen är
det något väldigt enkelt: en talföljd är helt enkelt en följd
av tal $a_{1},a_{2},a_{3},\ldots$. Talen $a_{n}$, som kallas
följdens element, kan vara heltal, reella tal
eller komplexa tal och följden kan vara ändlig eller oändlig, även om
det senare är det vanligaste i matematiken. När man
allmänt diskuterar talföljder så brukar numreringen av elementen
$a_{n}$ börja på $n=1$, men det är inte nödvändigt; ibland kan det
vara ändamålsenligt att numrera dem på något annat sätt. Det finns
flera olika sätt att definiera elementen i en talföljd:
- Med hjälp av en formel som i Exempel 2.1 och 2.2.
- Rekursivt, vilket innebär att $a_{n}$ uttrycks med hjälp
av ett eller flera av de föregående elementen. Följderna i Exempel 2.9, 2.10 och 2.11 är rekursivt definierade.
- Genom någon egenskap, t ex att kvoten mellan två på varandra
följande element alltid har samma värde (dvs en geometrisk talföljd, se nedan och boken Exempel 2.5 samt avsnitt 2.2).
- På något annat, mer eller mindre fantasifullt sätt. Exempelvis
skulle man kunna låta $a_{n}$ vara antalet bokstäver i ord nummer $n$ i Krig och fred. Tolstojs roman är visserligen ganska tjock, men följden blir förstås ändå ändlig.
Däremot kan man inte säga att en talföljd är given om man bara ger några termer, som t.ex. i Exempel 2.5. Vad punkterna står för kan man bara gissa. Det kan vara formeln som står i boken som bestämmer talföljden, dvs att nästa tal fås genom att multiplicera föregående tal med 3, men det skulle kunna vara något helt annat. En annan formel som stämmer är
an = 2 + 4(n − 1) + 4(n − 1)(n − 2) + 8 / 3(n − 1)(n − 2)(n − 3)
(kontrollera gärna genom att stoppa in $n=1,2,3,4$) men då skulle det gälla att a5 = 130 och inte $3\cdot54=162$. I själva verket kan man för ett godtyckligt antal termer alltid hitta ett polynomuttryck av ovanstående typ, så att formeln stämmer för dessa termer. I övning 2.2 är alltså de svar som anges i facit bara förslag, det finns andra svar som är lika korrekta.
Avsnitt 2.2
Aritmetiska följder och summor är, till skillnad från geometriska,
inte så vanliga i tillämpningar. Sats 2.2 är därför betydligt
viktigare än Sats 2.1. Ett sätt att komma ihåg formeln i Sats 2.1 är att lära sig följande sätt att läsa formeln:
antalet termer gånger första plus sista genom två
Observera att de $n$ första talen i den geometriska talföljden $a, ak,ak^2,ak^3,\ldots,ak^n,\ldots$, som det står om i Sats 2.2, är $a, ak,ak^2,ak^3,\ldots,ak^{n-1}$. Den n:te termen är alltså $ak^{n-1}$ och inte $ak^{n}$. Formeln för summan i fallet $k\ne1$ kan skrivas
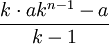
och därför kan man lära sig följande läsning av fomeln i Sats 2.2
k gånger sista minus första genom k minus 1
Detta kan med fördel användas t.ex. när man skall lösa Testproblem 3 d).
Sist i Sats 2.1 och 2.2 står en mening som inte är så bra formulerad. I Sats 2.1 bör den lyda så här i stället: "Summan $S_n$ kallas en aritmetisk summa."
Och i Sats 2.2 bör den lyda så här: "Summan $S_n$ kallas en geometrisk summa."
Efter Exempel 2.17 införs det viktiga
begreppet serie. En summa har alltid bara ändligt många
termer, medan en serie kan ha oändligt många. Eftersom man inte kan
lägga ihop oändligt många termer, så är det inte självklart vad man
skall mena med "summan av en serie". I kapitlet om gränsvärden kommer
detta att diskuteras. Att man måste vara aktsam när man manipulerar
serier framgår av följande halsbrytande räkning:
Betrakta talföljden $a_{n}=(-1)^n$, $n=0,1,2,\ldots$ och motsvarande serie $a_{0}+a_{1}+a_{2}+\ldots=1-1+1-1+1-1+\ldots$. Låt oss sätta in parenteser på två olika sätt och försöka räkna ut summan: å ena sidan är $$ 1-1+1-1+1-1+\ldots =(1-1)+(1-1)+(1-1)+\ldots=0+0+0+\ldots =0$$ och å den andra sidan är $$ 1-1+1-1+1-1+\ldots =1-(1-1)-(1-1)-\ldots=1-0-0-\ldots =1$$
Har vi funnit en motsägelse i matematiken? Nej, lösningen på den här paradoxen är att man får inte manipulera serier på samma sätt som ändliga summor.
Avsnitt 2.3
Summasymbolen $\sum$ känner du förmodligen till sedan tidigare, och om
inte, så är det bra om du lär dig använda den nu. Produkttecknet $\prod$ är ett stort pi. En
särskilt viktig produkt är fakulteten $n!$ som definieras på sid 71.
Således är $1!=1$ (då har produkten bara en enda faktor), $2!=1\cdot 2=2$, $3!=1\cdot 2\cdot 3=6$ osv. Räkna ut $4!$, $5!$ och $6!$ själv. Observera att för $n\ge 2$ gäller
$$ n!=1\cdot 2\cdot 3\cdot\ldots \cdot (n-1)\cdot n=(n-1)!\cdot n$$
Den här formeln kan man använda man för att motivera definitionen av $0!$ på sid 78. Om vi vill
att formeln skall gälla även då $n=1$, så måste
$$ 1!=(1-1)!\cdot 1=0!$$
och därför väljer man att definiera $0!$ som 1. Jämför detta med hur man gör för att definiera $a^0$.
Fakulteter uppträder naturligt i många matematiska sammanhang, som du kommer att se i kursen. En tillämpning är att $n!$ är antalet sätt man kan ordna $n$ element. T.ex. kan fem personer ordna upp sig i en kö på $5!=120$ sätt. En annan tillämpning finns på sid 222, som behandlar högre derivator: Låt $f(x)=(1+x)^n$, där $n$ är ett positivt heltal, dvs $n=1,2,3,\ldots$. Deriverar vi $f$ upprepade gånger så får vi
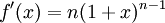

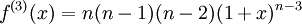
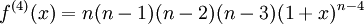
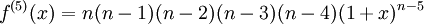
och allmänt
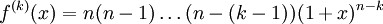
(beteckningen $f^{(k)}$ betyder alltså derivatan av ordning $k$ till
$f$). Derivatan av ordning $n$ blir således

Även produkten $n(n-1)\ldots (n-(k-1))$ kan uttryckas med hjälp av
fakulteter:
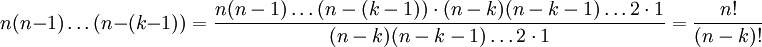
Sammanfattningsvis är alltså
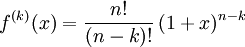
Avsnitt 2.5
Ett binom är ett uttryck med två termer, t ex $a+b$. Enligt
kvadreringsregeln är
$$ (a+b)^2=a^2+2ab+b^2$$
och "kuberingsregeln" säger att
$$ (a+b)^3=a^3+3a^2b+3ab^2+b^3$$
Jämför detta med "första kubregeln" på sid 42 som säger att $a^3+b^3=(a+b)(a^2-ab+b^2)$ vilket är något helt annat än "kuberingsregeln". Det gäller alltså inte att $(a+b)^3=a^3+b^3$ (och inte heller att $(a+b)^2=a^2+b^2$).
Den viktiga binomialsatsen, som formuleras i Sats 2.5 och längst ned på sid 81, är generaliseringen av de här formlerna till högre potenser $(a+b)^n$.
Studera utvecklingarna på sid 76. Hur får man t.ex. den sista raden från raden ovanför? Jo, de fyra termerna i utvecklingen av $(a+b)^3$ skall alla multipliceras med dels $a$ och dels $b$. Hur uppstår då termer på formen $a^2b^2$? Jo, genom att antingen multiplicera termen $3a^2b$ med $b$ eller att multiplicera termen $3ab^2$ med $a$ (och summera). Alltså förstår vi att talet 6 framför $a^2b^2$ har uppkommit genom att summera de två treorna på raden ovanför. På samma sätt ser vi att fyran framför $a^3b$ (eller framför $ab^3$) uppstår genom att summera ettan och trean på raden ovanför. Ettan längst till vänster (eller höger) uppstår genom att föra ned ettan på raden ovanför (och om man så vill summera en osynlig nolla).
Man inser att detta är ett generellt sätt att resonera, så vi kan nu lätt hitta utvecklingen av $(a+b)^5$ genom att summera intilliggande tal i den sista raden. Då får vi koefficienterna 1, 5, 10, 10, 5, 1 (och vi har därmed genomfört uppmaningen i boken efter utvecklingarna). Utan att snegla på sid 77, så kan du försöka skriva upp raden av koefficienter i utvecklingen av $(a+b)^6$.
Boken inför nu beteckningen  som utläses "n över k" och kallas binomialkoefficienter och som alltså är en beteckning för koefficienten framför $a^{n-k}b^k$ i utvecklingen av $(a+b)^n$. Utvecklingen av $(a+b)^4$ kan alltså skrivas
som utläses "n över k" och kallas binomialkoefficienter och som alltså är en beteckning för koefficienten framför $a^{n-k}b^k$ i utvecklingen av $(a+b)^n$. Utvecklingen av $(a+b)^4$ kan alltså skrivas
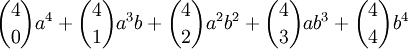
och allmänt gäller utvecklingen som står längst ned på sid 81, med eller utan användning av summa-symbolen. Eftersom första och sista koefficienten alltid är 1 och eftersom utvecklingen är symmetrisk (det blir samma om man läser från vänster eller höger), så har vi följande samband
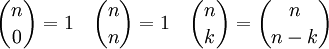
Dessutom gäller den viktiga egenskapen II. som står i rutan på sid 81. Det är den egenskapen som vi diskuterade oss fram till ovan och som bestämmer koefficienterna rad för rad. Om vi placerar binomialkoefficienterna i form av "Pascals triangel" som på sid 77, så kan alltså denna egenskap utläsas som
en binomialkoefficient är summan av dess två grannar på raden ovanför i Pascals traingel
Binomialkoefficienten  kan också ges en kombinatorisk tolkning. Den utgör antalet sätt att välja $k$ element ur $n$ element (utan att ta hänsyn till ordningen mellan elementen). Till exempel finns det
kan också ges en kombinatorisk tolkning. Den utgör antalet sätt att välja $k$ element ur $n$ element (utan att ta hänsyn till ordningen mellan elementen). Till exempel finns det 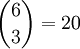 sätt att bland sex personer välja en kommitté bestående av tre personer (utan inbördes rangordning). Om en provfråga har fem svarsalternativ och man vet att precis två är rätt, så behövs maximalt
sätt att bland sex personer välja en kommitté bestående av tre personer (utan inbördes rangordning). Om en provfråga har fem svarsalternativ och man vet att precis två är rätt, så behövs maximalt 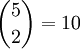 försök innan man fått rätt svar. Det är inte så konstigt att binomialkoefficienterna har denna tolkning, eftersom utvecklingen av $(a+b)^n$ fås genom att multiplicera ihop $n$ st parenteser $(a+b)$ och detta sker genom att ur varje parentes välja antingen $a$ eller $b$ (och multiplicera). Antalet termer på formen $a^{n-k}b^{k}$ är därför antalet sätt att välja ut $k$ parenteser ur $n$ (de parenteser där man väljer $b$).
försök innan man fått rätt svar. Det är inte så konstigt att binomialkoefficienterna har denna tolkning, eftersom utvecklingen av $(a+b)^n$ fås genom att multiplicera ihop $n$ st parenteser $(a+b)$ och detta sker genom att ur varje parentes välja antingen $a$ eller $b$ (och multiplicera). Antalet termer på formen $a^{n-k}b^{k}$ är därför antalet sätt att välja ut $k$ parenteser ur $n$ (de parenteser där man väljer $b$).
Nu kan vi det mesta man behöver veta om binomialsatsen och binomialkoefficienterna, men det finns ytterligare en nyttig sak att lära sig, nämligen en explicit formel för binomialkoefficienterna. För att i praktiken räkna ut binomialkoefficienter så duger Pascals triangel utmärkt, men i vissa teoretiska ssammanhang så ger en formel mer information. Formeln som jag tänker på hittar du överst på sid 78. Genom att förkorta med $(n-k)!$ kan formeln också skrivas
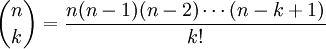
Ett sätt att kombinatoriskt resonera sig fram till att denna formel uttrycker antalet sätt att välja $k$ parenteser bland $n$ parenteser är följande (=överkurs).
Den första parentesen kan väljas på $n$ sätt. Oberoende av det valet kan vi välja nästa parentes på $n-1$ sätt, dvs de två första parenteserna kan väljas på $n(n-1)$ sätt. Fortsätter man på detta sätt finner man att man kan välja $k$ parenteser i ordning bland $n$ parenteser på $n(n-1)(n-2)\cdots(n-k+1)$ sätt. Men vi är inte intresserade av vilken ordning vi väljer parenteserna. Det går att ordna $k$ parenteser på $k!$ sätt (se ovan). Alltså kommer varje val av $k$ parenteser att räknas $k!$ gånger, vilket motiverar att vi skall dividera med $k!$ för att få svaret.
Bokens bevis går ut på följande (också överkurs). Inför beteckningen 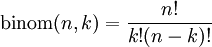 . Vi vill alltså visa att
. Vi vill alltså visa att  . Genom att stoppa in $k=0$ och $k=n$ i formeln (och utnyttja definitionen $0!=1$) så får vi att
${\rm binom}(n,0)={\rm binom}(n,n)=1$. Lemma 2.1 säger att ${\rm binom}(n+1,k)={\rm binom}(n,k)+{\rm binom}(n,k-1)$. Detta betyder att ${\rm binom}(n,k)$ kan beräknas successivt på samma sätt som
. Genom att stoppa in $k=0$ och $k=n$ i formeln (och utnyttja definitionen $0!=1$) så får vi att
${\rm binom}(n,0)={\rm binom}(n,n)=1$. Lemma 2.1 säger att ${\rm binom}(n+1,k)={\rm binom}(n,k)+{\rm binom}(n,k-1)$. Detta betyder att ${\rm binom}(n,k)$ kan beräknas successivt på samma sätt som  via Pascals triangel och de måste därför vara lika.
via Pascals triangel och de måste därför vara lika.
Låt oss till slut föregripa lite om "Maclaurinserier" (se sid 220) och kombinera resultatet ovan om de högre derivatorna av funktionen $f(x)=(1+x)^n$ med binomialsatsen. Enligt ovan har vi att
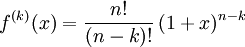
för $k\le n$ och $\displaystyle f^{(k)}(x)=0$ för $k>n$. Alltså gäller

för $k\le n$ och $\displaystyle f^{(k)}(0)=0$ för $k>n$ vilket ger att
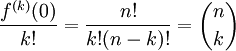
för $k\le n$ och
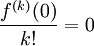
för $k>n$. Maclaurinserien för funktionen $f$ är därför
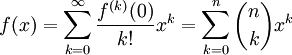
medan binomialsatsen tillämpad på $f(x)=(1+x)^n$ ger
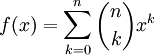
Vi får alltså samma resultat, vilket ju känns tryggt.
Lämpliga övningsuppgifter till Lektion 4
Välj bland följande uppgifter i boken: 2.1-2.2, 2.4-2.23, 2.30-2.35

