Lektion 3
Matematik för naturvetare 15hp
| Versionen från 23 augusti 2007 kl. 09.53 (redigera) KTH.SE:u17xlk1r (Diskussion | bidrag) (Ny sida: ==Välkommen till Lektion #!== I den här lektionen... Du ska studera följande kapitel i boken: * '''Viktiga saker att tänka på när du läser''' '''Lämpliga övningsuppgifter t...) ← Gå till föregående ändring |
Nuvarande version (25 augusti 2007 kl. 16.20) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag) |
||
| (4 mellanliggande versioner visas inte.) | |||
| Rad 1: | Rad 1: | ||
| - | ==Välkommen till Lektion #!== | + | [[Läsanvisningar | Tillbaka till läsanvisningarna]] |
| - | I den här lektionen... | + | ==Välkommen till Lektion 3!== |
| + | |||
| + | I den här lektionen ska vi studera potenser, logaritmer, formler och kurvritning. | ||
| Du ska studera följande kapitel i boken: | Du ska studera följande kapitel i boken: | ||
| - | * | + | * 1.5 Potenser |
| + | * 1.6 Logaritmer | ||
| + | * 1.8 Formler och kurvritning | ||
| '''Viktiga saker att tänka på när du läser''' | '''Viktiga saker att tänka på när du läser''' | ||
| + | |||
| + | I avsnitt 1.5 behandlas potenser $a^b$ där $a$ är ett positivt reellt tal och $b$ är ett godtyckligt reellt tal. Komplettera gärna bokens framställning med stencilen Potenser. Definitionen i boken av potenser görs bara i fallet att $b$ är ett positivt heltal, eller 0 eller -1. Definitionen av $a^b$ då $b$ är ett negativt heltal och då $b$ är ett rationellt tal är som följer. | ||
| + | |||
| + | $$a^{-n}=1/a^n\quad\text{om }n\text{ är ett positivt heltal}$$ | ||
| + | |||
| + | $$a^{p/q}=\root{q}\of{a^p}\quad\text{om }q\text{ är ett positivt heltal och }p\text{ är ett heltal}$$ | ||
| + | |||
| + | Vidare gäller att $\root{q}\of{c}$ definieras som den entydiga positiva lösningen till ekvationen $x^q=c$. | ||
| + | |||
| + | Definitionen av $a^b$ då $b$ är irrationellt görs med hjälp av gränsvärden. Det irrationella talet $b$ kan approximeras godtyckligt noggrant med rationella tal (t.ex. genom decimalutveckling av $b$). | ||
| + | |||
| + | Nu kan du göra övning 1.16, dvs bevisa Sats 1.2 för rationella exponenter (men det är inte någon enkel uppgift, kanske kan det räcka med att bevisa satsen för godtyckliga heltal, börja i så fall med positiva heltal och låt sedan b och/eller c vara negativa heltal eller 0). | ||
| + | |||
| + | I Sats 1.2 kan man också lägga till ytterligare en lag, nämligen | ||
| + | |||
| + | $$(ab)^c=a^c*b^c \quad\text{där }a>0\text{ och }b>0$$ | ||
| + | |||
| + | |||
| + | Logaritmer behöver man när man skall lösa ekvationer där den obekanta står som exponent, t.ex. <math>2^x=10</math>. Man kan visa att det finns precis ett reellt tal som löser ekvationen och detta tal skrives <math>\log_210</math> och utläses "två-logaritmen för tio". Det gäller alltså att "två-logaritmen för tio" är "det tal som två skall upphöjas till för att bli tio". Det är bra att lära sig den frasen utantill (med möjlighet förstås att byta ut två och tio mot andra positiva tal). Exempelvis är "tre-logaritmen för sju" lika med "det tal som tre skall upphöjas till för att bli sju", det skrives <math>\log_37</math> och är lösningen till ekvationen <math>3^x=7</math>; "pi-logaritmen för e" är "det tal som pi skall upphöjas till för att bli e", det skrives $\log_\pi e$ och är lösningen till ekvationen $\pi^x=e$. Ett närmevärde kan man få genom att använda något räknetekniskt hjälpmedel, t.ex. gäller $\log_37\approx1,77$, $3^{1,77}\approx6,99$; $\log_\pi e\approx0,87$, $\pi^{0,87}\approx2,71$; $\log_210\approx3,32$, $2^{3,32}\approx9,99$. | ||
| + | |||
| + | Det finns en analogi mellan logaritmer och rötter. Rötter behöver man när man skall lösa ekvationer av typen <math>x^2=10</math>, <math>x^3=7</math>, $x^\pi=e$ där <math>x</math> är ett positivt tal. Lösningen till <math>x^3=7</math> skrives $\root{3}\of{7}$ och utläses "tredje roten ur sju" och är alltså "det tal som upphöjt till tre blir sju" (jämför detta med frasen ovan som beskriver tre-logaritmen för sju). Lösningen till $x^\pi=e$ skrives $\root{\pi}\of{e}$ och utläses "pi:te roten ur e" och är alltså "det tal som upphöjt till pi blir e". Lösningen till <math>x^2=10</math> skrives $\sqrt{10}$ och utläses "(kvadrat)roten ur tio" (man utelämnar alltså tvåan i det här fallet) och är alltså "det tal som upphöjt till två blir tio". (Observera att vi förutsätter att $x$ är ett positivt tal. Lösningen till ekvationen $x^2=10$ där $x$ är ett godtyckligt reellt tal är $x=\pm\sqrt{10}$.) Även här kan man använda ett räknetekniskt hjälpmedel för att få närmevärden, t.ex. $\root{3}\of{7}\approx1,91$, $1,91^3\approx6,97$; $\root{\pi}\of{e}\approx1,37$, $1,37^\pi\approx2,69$; $\sqrt{10}\approx3,16$, $3,16^2\approx9,99$. | ||
| + | |||
| + | Något som skiljer logaritmer och rötter åt, är att rötter alltid är positiva medan en logaritm kan vara negativ. Det gäller exempelvis att <math>3^{-2}=1/9</math> och därför gäller att tre-logaritmen för <math>1/9</math> är <math>-2</math>, <math>\log_3(1/9)=-2</math>. Genom att utnyttja egenskaper för potenser (Sats 1.2) kan man härleda räknelagar för logaritmer (Sats 1.3). Den första logaritmlagen "motsvarar" den första potenslagen. Vi ger här ett bevis för den första logaritmlagen och lämnar beviset av den andra som övning. | ||
| + | |||
| + | Det gäller alltså att bevisa att | ||
| + | |||
| + | $$\log_a(c\cdot d)=\log_ac+\log_ad$$ | ||
| + | |||
| + | Sätt <math>x=\log_ac</math> och <math>y=\log_ad</math>. Då gäller <math> a^x=c</math> och <math>a^y=d</math>. Enligt första potenslagen gäller <math> a^{x+y}=a^x\cdot a^y</math>. Alltså gäller <math>a^{x+y}=c\cdot d</math>. Enligt definitionen av logaritmer gäller därför att <math>\log_a(c\cdot d)=x+y</math>. Om vi nu stoppar in vad <math>x</math> och <math>y</math> är så får vi det som vi skulle bevisa. | ||
| + | |||
| + | |||
| + | Den sjätte logaritmlagen i Sats 1.3 kan skrivs om på formen | ||
| + | |||
| + | <math>\log_bM=\frac{\log_aM}{\log_ab}</math> | ||
| + | |||
| + | som kan användas för att uttrycka en b-logaritm i a-logaritmer. | ||
| + | |||
| + | Det finns två baser för logaritmer som används oftare än andra, nämligen basen 10 och basen e (jämför fallet med rötter, där kvadratroten är den vanligaste). Som beteckning för 10-logaritmer används lg och som beteckning för e-logaritmer (som också kallas "naturliga logaritmer") används ln. Basen 10 är speciell på grund av att vi använder 10 som bas i vårt positionssystem för att beteckna tal. Tiopotenser är ju "byggstenarna" i talsystemet. Det gäller t.ex. att 10-logaritmen för 1000 är 3, eftersom <math>10^3=1000</math>. Däremot kan 2-logaritmen för 1000 inte anges exakt. Ett exakt värde har istället 2-logaritmen för 1024, nämligen 10, eftersom <math>2^{10}=1024</math>. | ||
| + | |||
| + | Följdsats 1.3 är en tillämpning av regel VI i Sats 1.3, men det är inte uppenbart hur. Den andra formeln | ||
| + | |||
| + | <math>\log_ab=\frac{\ln b}{\ln a}</math> | ||
| + | |||
| + | får man från omskrivningen ovan genom att ersätta a med e och därefter ersätta b med a och M med b. Den första formeln | ||
| + | |||
| + | $$\log_ab=\log_ae\cdot\ln b$$ | ||
| + | |||
| + | får man från regel VI genom att ersätta b med e och därefter M med b (och multiplicera upp nämnaren). | ||
| + | |||
| + | Exempel 1.13 innehåller exempel på exakt beräkning av logaritmer. Den fjärde likheten i lösningen av f) använder sig av regel III i Sats 1.3 (med $c= \log_52$). | ||
| + | |||
| + | I lösningen av Exempel 1.16 ska kommentaren "Vi logaritmerar bägge leden!" placeras på raden ovanför. Något enklare hade det varit att använda 10-logaritemer. Då blir tredje raden $\lg2^{n-1}=\lg10^5=5$. Nästa rad blir då $(n-1)\lg2=5$, varav det följer att $n=5/\lg2+1$. | ||
| + | |||
| + | |||
| + | Att basen e för logaritmer är "naturlig" beror fämst på att derivatan av funktionen $y=\log_ax$ är speciellt enkel för a=e (se Sats 6.2 sid 173). Naturliga logaritmer förekommer också vid beräkning av integraler (se Exempel 9.6 sid 232) och vid lösning av differentialekvationer (se Exempel 13.14 sid 344). | ||
| - | '''Lämpliga övningsuppgifter till Lektion #''' | + | '''Lämpliga övningsuppgifter till Lektion 3''' |
| - | Välj bland följande uppgifter i boken: | + | Välj bland följande uppgifter i boken: 1.13-1.15, 1.19, 1.21-1.23, 1.27 c) d), 1.29-1.31, 1.35, 1.39-1.42 (den fysikintresserade studenten kan även vilja titta på uppgifterna 1.34, 1.36-1.39) |
| [[Läsanvisningar | Tillbaka till läsanvisningarna]] | [[Läsanvisningar | Tillbaka till läsanvisningarna]] | ||
Nuvarande version
Tillbaka till läsanvisningarna
[redigera] Välkommen till Lektion 3!
I den här lektionen ska vi studera potenser, logaritmer, formler och kurvritning.
Du ska studera följande kapitel i boken:
- 1.5 Potenser
- 1.6 Logaritmer
- 1.8 Formler och kurvritning
Viktiga saker att tänka på när du läser
I avsnitt 1.5 behandlas potenser $a^b$ där $a$ är ett positivt reellt tal och $b$ är ett godtyckligt reellt tal. Komplettera gärna bokens framställning med stencilen Potenser. Definitionen i boken av potenser görs bara i fallet att $b$ är ett positivt heltal, eller 0 eller -1. Definitionen av $a^b$ då $b$ är ett negativt heltal och då $b$ är ett rationellt tal är som följer.
$$a^{-n}=1/a^n\quad\text{om }n\text{ är ett positivt heltal}$$
$$a^{p/q}=\root{q}\of{a^p}\quad\text{om }q\text{ är ett positivt heltal och }p\text{ är ett heltal}$$
Vidare gäller att $\root{q}\of{c}$ definieras som den entydiga positiva lösningen till ekvationen $x^q=c$.
Definitionen av $a^b$ då $b$ är irrationellt görs med hjälp av gränsvärden. Det irrationella talet $b$ kan approximeras godtyckligt noggrant med rationella tal (t.ex. genom decimalutveckling av $b$).
Nu kan du göra övning 1.16, dvs bevisa Sats 1.2 för rationella exponenter (men det är inte någon enkel uppgift, kanske kan det räcka med att bevisa satsen för godtyckliga heltal, börja i så fall med positiva heltal och låt sedan b och/eller c vara negativa heltal eller 0).
I Sats 1.2 kan man också lägga till ytterligare en lag, nämligen
$$(ab)^c=a^c*b^c \quad\text{där }a>0\text{ och }b>0$$
Logaritmer behöver man när man skall lösa ekvationer där den obekanta står som exponent, t.ex. 2x = 10. Man kan visa att det finns precis ett reellt tal som löser ekvationen och detta tal skrives log210 och utläses "två-logaritmen för tio". Det gäller alltså att "två-logaritmen för tio" är "det tal som två skall upphöjas till för att bli tio". Det är bra att lära sig den frasen utantill (med möjlighet förstås att byta ut två och tio mot andra positiva tal). Exempelvis är "tre-logaritmen för sju" lika med "det tal som tre skall upphöjas till för att bli sju", det skrives log37 och är lösningen till ekvationen 3x = 7; "pi-logaritmen för e" är "det tal som pi skall upphöjas till för att bli e", det skrives $\log_\pi e$ och är lösningen till ekvationen $\pi^x=e$. Ett närmevärde kan man få genom att använda något räknetekniskt hjälpmedel, t.ex. gäller $\log_37\approx1,77$, $3^{1,77}\approx6,99$; $\log_\pi e\approx0,87$, $\pi^{0,87}\approx2,71$; $\log_210\approx3,32$, $2^{3,32}\approx9,99$.
Det finns en analogi mellan logaritmer och rötter. Rötter behöver man när man skall lösa ekvationer av typen x2 = 10, x3 = 7, $x^\pi=e$ där x är ett positivt tal. Lösningen till x3 = 7 skrives $\root{3}\of{7}$ och utläses "tredje roten ur sju" och är alltså "det tal som upphöjt till tre blir sju" (jämför detta med frasen ovan som beskriver tre-logaritmen för sju). Lösningen till $x^\pi=e$ skrives $\root{\pi}\of{e}$ och utläses "pi:te roten ur e" och är alltså "det tal som upphöjt till pi blir e". Lösningen till x2 = 10 skrives $\sqrt{10}$ och utläses "(kvadrat)roten ur tio" (man utelämnar alltså tvåan i det här fallet) och är alltså "det tal som upphöjt till två blir tio". (Observera att vi förutsätter att $x$ är ett positivt tal. Lösningen till ekvationen $x^2=10$ där $x$ är ett godtyckligt reellt tal är $x=\pm\sqrt{10}$.) Även här kan man använda ett räknetekniskt hjälpmedel för att få närmevärden, t.ex. $\root{3}\of{7}\approx1,91$, $1,91^3\approx6,97$; $\root{\pi}\of{e}\approx1,37$, $1,37^\pi\approx2,69$; $\sqrt{10}\approx3,16$, $3,16^2\approx9,99$.
Något som skiljer logaritmer och rötter åt, är att rötter alltid är positiva medan en logaritm kan vara negativ. Det gäller exempelvis att 3 − 2 = 1 / 9 och därför gäller att tre-logaritmen för 1 / 9 är − 2, log3(1 / 9) = − 2. Genom att utnyttja egenskaper för potenser (Sats 1.2) kan man härleda räknelagar för logaritmer (Sats 1.3). Den första logaritmlagen "motsvarar" den första potenslagen. Vi ger här ett bevis för den första logaritmlagen och lämnar beviset av den andra som övning.
Det gäller alltså att bevisa att
$$\log_a(c\cdot d)=\log_ac+\log_ad$$
Sätt x = logac och y = logad. Då gäller ax = c och ay = d. Enligt första potenslagen gäller 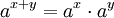 . Alltså gäller
. Alltså gäller 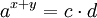 . Enligt definitionen av logaritmer gäller därför att
. Enligt definitionen av logaritmer gäller därför att 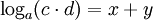 . Om vi nu stoppar in vad x och y är så får vi det som vi skulle bevisa.
. Om vi nu stoppar in vad x och y är så får vi det som vi skulle bevisa.
Den sjätte logaritmlagen i Sats 1.3 kan skrivs om på formen

som kan användas för att uttrycka en b-logaritm i a-logaritmer.
Det finns två baser för logaritmer som används oftare än andra, nämligen basen 10 och basen e (jämför fallet med rötter, där kvadratroten är den vanligaste). Som beteckning för 10-logaritmer används lg och som beteckning för e-logaritmer (som också kallas "naturliga logaritmer") används ln. Basen 10 är speciell på grund av att vi använder 10 som bas i vårt positionssystem för att beteckna tal. Tiopotenser är ju "byggstenarna" i talsystemet. Det gäller t.ex. att 10-logaritmen för 1000 är 3, eftersom 103 = 1000. Däremot kan 2-logaritmen för 1000 inte anges exakt. Ett exakt värde har istället 2-logaritmen för 1024, nämligen 10, eftersom 210 = 1024.
Följdsats 1.3 är en tillämpning av regel VI i Sats 1.3, men det är inte uppenbart hur. Den andra formeln

får man från omskrivningen ovan genom att ersätta a med e och därefter ersätta b med a och M med b. Den första formeln
$$\log_ab=\log_ae\cdot\ln b$$
får man från regel VI genom att ersätta b med e och därefter M med b (och multiplicera upp nämnaren).
Exempel 1.13 innehåller exempel på exakt beräkning av logaritmer. Den fjärde likheten i lösningen av f) använder sig av regel III i Sats 1.3 (med $c= \log_52$).
I lösningen av Exempel 1.16 ska kommentaren "Vi logaritmerar bägge leden!" placeras på raden ovanför. Något enklare hade det varit att använda 10-logaritemer. Då blir tredje raden $\lg2^{n-1}=\lg10^5=5$. Nästa rad blir då $(n-1)\lg2=5$, varav det följer att $n=5/\lg2+1$.
Att basen e för logaritmer är "naturlig" beror fämst på att derivatan av funktionen $y=\log_ax$ är speciellt enkel för a=e (se Sats 6.2 sid 173). Naturliga logaritmer förekommer också vid beräkning av integraler (se Exempel 9.6 sid 232) och vid lösning av differentialekvationer (se Exempel 13.14 sid 344).
Lämpliga övningsuppgifter till Lektion 3
Välj bland följande uppgifter i boken: 1.13-1.15, 1.19, 1.21-1.23, 1.27 c) d), 1.29-1.31, 1.35, 1.39-1.42 (den fysikintresserade studenten kan även vilja titta på uppgifterna 1.34, 1.36-1.39)

