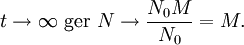Lösningar 19

Matematik för naturvetare 15hp

Versionen från 2 oktober 2007 kl. 13.35 (redigera) Clas Löfwall (Diskussion | bidrag) (Ny sida: ==Lösningar till några övningar till lektion 19== Tillbaka till lösningarna) ← Gå till föregående ändring		Nuvarande version (16 oktober 2007 kl. 15.37) (redigera) (ogör) Clas Löfwall (Diskussion | bidrag)
(8 mellanliggande versioner visas inte.)
Rad 2:		Rad 2:
	[[Exempellösningar|Tillbaka till lösningarna]]		[[Exempellösningar|Tillbaka till lösningarna]]
		+
		+
		+
		+
		+	'''11.1.'''
		+
		+	Att bestämma partialbråksuppdelningar utan ansats är förstås
		+	tramsigt eftersom man i praktiken alltid använder olika ansatser. Lös
		+	därför övningen hur du vill!
		+
		+
		+
		+	'''11.1.a)'''
		+
		+	<math>
		+	\frac{1}{x(x+1)}=\frac{(x+1)-x}{x(x+1)}=\frac{x+1}{x(x+1)}-\frac{x}{x(x+1)}=
		+	\frac{1}{x}-\frac{1}{x+1}</math>
		+
		+
		+
		+	'''11.1.b)'''
		+
		+	<math>\begin{array}{lll}
		+	\frac{1}{x^2(x-1)}&=&\frac{x^2-(x^2-x)-(x-1)}{x^2(x-1)}=
		+	\frac{x^2}{x^2(x-1)}-\frac{x(x-1)}{x^2(x-1)}-\frac{x-1}{x^2(x-1)}\\
		+	&=&
		+	\frac{1}{x-1}-\frac{1}{x}-\frac{1}{x^2}\end{array}</math>
		+
		+
		+
		+	'''11.1.c)'''
		+
		+	<math>
		+	\frac{1}{x(4x^2+1)}=\frac{4x^2+1-4x^2}{x(4x^2+1)}=
		+	\frac{4x^2+1}{x(4x^2+1)}-\frac{4x^2}{x(4x^2+1)}=
		+	\frac{1}{x}-\frac{4x}{4x^2+1}</math>
		+
		+
		+
		+	'''11.2.a.'''
		+
		+	<math>
		+	\int\frac{dx}{x(x+1)}=\int\left(\frac{1}{x}-\frac{1}{x+1}\right)\, dx=
		+	\ln |x|-\ln|x+1|+C=\ln\left|\frac{x}{x+1}\right|+C</math>
		+
		+
		+
		+	'''11.2.b)'''
		+
		+	<math>
		+	\int\frac{dx}{x^2(x-1)}=\int\left(
		+	\frac{1}{x-1}-\frac{1}{x}-\frac{1}{x^2}\right)\, dx=
		+	\ln|x-1|-\ln |x|+\frac{1}{x}+C</math>
		+
		+
		+
		+	'''11.2.c)'''
		+
		+	<math>\begin{array}{lll}
		+	\int\frac{dx}{x(4x^2+1)}&=&\int\left(\frac{1}{x}-\frac{4x}{4x^2+1}\right)\, dx=
		+	\ln|x|-\frac{1}{2}\int\frac{8x}{4x^2+1}\, dx\\
		+	&=&
		+	\ln
		+	|x|-\frac{1}{2}\ln|4x^2+1|+C=\ln\frac{|x|}{\sqrt{4x^2+1}}+C\end{array}</math>
		+
		+
		+
		+	'''11.6.a.'''
		+
		+	Vi har $9-x^2=(3+x)(3-x)$ så uppdelningen har utseendet
		+
		+	<math>
		+	\frac{3}{9-x^2}=\frac{A}{3+x}+\frac{B}{3-x}.</math>
		+
		+
		+	Vi gör liknämnigt:
		+
		+	<math>
		+	\frac{A}{3+x}+\frac{B}{3-x}=\frac{B(3+x)+A(3-x)}{(3+x)(3-x)}=
		+	\frac{(-A+B)x+3(A+B)}{9-x^2}</math>
		+
		+
		+	Detta ger ekvationssystemet
		+
		+	<math>
		+	\left\{\begin{array}{cccc}
		+	-A+B&=&0\\
		+	A+B&=&1\end{array}\right.</math>
		+
		+
		+	som har lösningen $A=B=1/2$. Partialbråksuppdelningen är således
		+
		+	<math>
		+	\frac{3}{9-x^2}=\frac{1}{2}\left(\frac{1}{3+x}+\frac{1}{3-x}\right).</math>
		+
		+
		+
		+	'''11.6.b)'''
		+
		+	Vi faktoriserar nämnaren genom att bestämma dess nollställen:
		+
		+
		+	<math>
		+	6x-x^2-5=0\Leftrightarrow x^2-6x+5=0\Leftrightarrow
		+	x=3\pm\sqrt{9-5}=3\pm2</math>
		+
		+
		+	Nollställena är $x=1$ och $x=5$, så
		+
		+	<math>
		+	6x-x^2-5=-(x-1)(x-5)=(1-x)(x-5).</math>
		+
		+
		+	Partialbråksuppdelningen har utseendet
		+
		+	<math>
		+	\frac{1}{6x-x^2-5}=\frac{A}{1-x}+\frac{B}{x-5}</math>
		+
		+
		+	och gör vi liknämnigt så får vi
		+
		+	<math>
		+	\frac{A}{1-x}+\frac{B}{x-5}=\frac{A(x-5)+B(1-x)}{(1-x)(x-5)}=
		+	\frac{(A-B)x-5A+B}{6x-x^2+5}.</math>
		+
		+
		+	Alltså måste
		+
		+	<math>
		+	\left\{\begin{array}{ccc}
		+	A-B&=&0\\
		+	-5A+B&=&1\end{array}\right.
		+	\Leftrightarrow
		+	A=B=-\frac{1}{4}.</math>
		+
		+
		+	Detta ger
		+
		+	<math>
		+	\frac{1}{6x-x^2-5}=-\frac{1}{4}\left(\frac{1}{1-x}+\frac{1}{x-5}\right).</math>
		+
		+
		+
		+	'''11.6.c)'''
		+
		+	Nämnaren har faktoriseringen $x^3-1=(x-1)(x^2+x+1)$, där
		+	andragradsfaktorn inte har några reella nollställen (och således inte
		+	går att faktorisera vidare). Partialbråksuppdelningen har utseendet
		+
		+	<math>
		+	\frac{1}{x^3-1}=\frac{A}{x-1}+\frac{Bx+C}{x^2+x+1}.</math>
		+
		+
		+	Vi gör liknämnigt i HL:
		+
		+	<math>\begin{array}{lll}
		+	\frac{A}{x-1}+\frac{Bx+C}{x^2+x+1}&=&
		+	\frac{A(x^2+x+1)+(Bx+C)(x-1)}{(x-1)(x^2+x+1)}\\
		+	&=&
		+	\frac{(A+B)x^2+(A-B+C)x+A-C}{x^3-1}.\end{array}</math>
		+
		+
		+	Detta ger ekvationsystemet
		+
		+	<math>
		+	\left\{\begin{array}{cccccccccc}
		+	A&+&B&&&=&0\\
		+	A&-&B&+&C&=&0\\
		+	A&&&-&C&=&1\end{array}\right.\Leftrightarrow
		+	\left\{\begin{array}{cccc}
		+	A&=&1/3\\
		+	B&=&-1/3\\
		+	C&=&-2/3\end{array}\right.
		+	</math>
		+
		+
		+	och vi får till sist
		+
		+	<math>
		+	\frac{1}{x^3-1}=\frac{1}{3}\left(\frac{1}{x-1}-\frac{x+2}{x^2+x+1}\right).</math>
		+
		+
		+
		+	'''11.7.a)'''
		+
		+	<math>
		+	\int\frac{3}{9-x^2}\,
		+	dx=\frac{1}{2}\int\left(\frac{1}{3+x}-\frac{1}{x-3}\right)\, dx=
		+	\frac{1}{2}\left(\ln|x+3|-\ln|x-3|\right)+C</math>
		+
		+
		+
		+	'''11.7.b)'''
		+
		+	<math>\begin{array}{lll}
		+	\int\frac{dx}{6x-x^2-5}&=&\frac{1}{4}\int\left(
		+	\frac{1}{x-1}-\frac{1}{x-5}\right)\, dx\\
		+	&=&
		+	\frac{1}{4}\left(\ln|x-1|-\ln|x-5|\right)+C\end{array}</math>
		+
		+
		+
		+	'''11.7.c)'''
		+
		+	Vi skriver den andra termen i parentesen som
		+
		+	<math>
		+	\frac{x+2}{x^2+x+1}=\frac{1}{2}\left(
		+	\frac{2x+1}{x^2+x+1}+\frac{3}{x^2+x+1}\right).</math>
		+
		+
		+	Här har den första termen utseendet $f'(x)/f(x)$, där $f(x)=x^2+x+1$.
		+	En primitiv funktion är således $\ln|f(x)|=\ln(x^2+x+1)$ (observera
		+	att $x^2+x+1>0$ för alla $x$). För att integrera den andra termen
		+	kvadratkompletterar vi nämnaren:
		+
		+	<math>
		+	x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}=
		+	\frac{3}{4}\left(1+\left(\frac{2x+1}{\sqrt 3}\right)^2\right)</math>
		+
		+
		+	Alltså är
		+
		+	<math>
		+	\int\frac{dx}{x^2+x+1}=\frac{4}{3}\cdot\frac{\sqrt 3}{2}\arctan\frac{2x+1}{\sqrt
		+	3}+C=
		+	\frac{2}{\sqrt 3}\arctan\frac{2x+1}{\sqrt 3}+C</math>
		+
		+
		+	De primitiva funktionerna till $1/(x^3-1)$ är således
		+
		+	<math>
		+	\frac{1}{3}\left(\ln|x-1|-\frac{1}{2}\ln(x^2+x+1)-\sqrt 3
		+	\arctan\frac{2x+1}{\sqrt 3}\right)+C.
		+	</math>
		+
		+
		+
		+	'''11.9.b.'''
		+
		+	Partialbråksuppdela:
		+
		+	<math>
		+	\frac{x+3}{x(x+2)}=\frac{A}{x}+\frac{B}{x+2}=\frac{(A+B)x+2A}{x(x+2)}</math>
		+
		+
		+	Detta ger $A+B=1$, $2A=3$, alltså $A=3/2$, $B=-1/2$. Alltså
		+
		+
		+	<math>\begin{array}{lll}
		+	\int_{1}^2\frac{x+3}{x(x+2)}\, dx&=&
		+	\frac{1}{2}\int_{1}^2\left(\frac{3}{x}-\frac{1}{x+2}\right)\, dx
		+	=
		+	\frac{1}{2}\left[3\ln|x|-\ln|x+2|\right]_{1}^2\\
		+	&=&
		+	\frac{1}{2}(3\ln 2-\ln 4-3\ln 1+\ln 3)=
		+	\frac{1}{2}\ln 6\end{array}</math>
		+
		+
		+
		+	'''11.9.d)'''
		+
		+	Den andra faktorn kan faktoriseras: $x^2+2x-3=(x-1)(x+3)$.
		+	Partialbråksuppdelning:
		+
		+	<math>
		+	\frac{1}{(x+1)(x^2+2x-3)}=\frac{1}{(x+1)(x-1)(x+3)}=
		+	\frac{A}{x+1}+\frac{B}{x-1}+\frac{C}{x+3}.</math>
		+
		+
		+	Ekvationsystemet blir
		+
		+	<math>
		+	\left\{\begin{array}{ccccccc}
		+	A&+&B&+&C&=&0\\
		+	A&+&2B&&&=&0\\
		+	-3A&+&3B&-&C&=&1\end{array}\right.\Leftrightarrow
		+	\left\{\begin{array}{ccc}
		+	A&=&-1/4\\
		+	B&=&1/8\\
		+	C&=&1/8\end{array}\right.</math>
		+
		+
		+	Alltså
		+
		+	<math>\begin{array}{lll}
		+	\int\frac{dx}{(x+1)(x^2+2x-3)}&=&
		+	-\frac{1}{4}\ln|x+1|+\frac{1}{8}\ln|x-1|+\frac{1}{8}\ln|x+3|+C\\
		+	&=&
		+	\frac{1}{8}\ln\frac{|(x-1)(x+3)|}{(x+1)^2}+C\end{array}</math>
		+
		+
		+	Vi har
		+
		+	<math>
		+	\lim_{x\to\infty}\ln\frac{|(x-1)(x+3)|}{(x+1)^2}=
		+	\lim_{x\to\infty}\ln\frac{(1-1/x)(1+3/x)}{(1+1/x)^2}=
		+	\ln 1=0,</math>
		+
		+
		+	så
		+
		+	<math>\begin{array}{lll}
		+	\int_{2}^{\infty}\frac{dx}{(x+1)(x^2+2x-3)}&=&
		+	\left[\frac{1}{8}\ln\frac{|(x-1)(x+3)|}{(x+1)^2}\right]_{2}^{\infty}\\
		+	&=&
		+	-\frac{1}{8}\ln\frac{1\cdot
		+	5}{3^2}=\frac{1}{8}\ln\frac{9}{5}.\end{array}</math>
		+
		+
		+
		+	'''11.9.e)'''
		+
		+	Här är partialbråksuppdelningen
		+
		+	<math>
		+	\frac{17x^2-x-26}{(x^2-1)(x^2-4)}=\frac{1}{3}\left(
		+	-\frac{4}{x+1}+\frac{5}{x-1}-\frac{11}{x+2}+\frac{10}{x-2}\right)</math>
		+
		+	och integralen blir
		+
		+	<math>\begin{array}{lll}
		+	&\frac{1}{3}\left[-4\ln|x+1|+5\ln|x-1|-11\ln|x+2|+10\ln|x-2|\right]_{3}^4&\\
		+	&=\frac{1}{3}(7\ln 5-6\ln 3+2\ln 2).&\end{array}</math>
		+
		+
		+
		+	'''11.10.'''
		+
		+	Partialbråksuppdelning ger
		+
		+	<math>\begin{array}{lll}
		+	t&=&\int_{N_{0}}^{N}\frac{K\, dn}{n(M-n)}=
		+	\frac{K}{M}\int_{N_{0}}^{N}\left(\frac{1}{n}+\frac{1}{M-n}\right)\,
		+	dn\\
		+	&=&
		+	\frac{K}{M}\left[\ln |n|-\ln|M-n|\right]_{N_{0}}^{N}=
		+	\frac{K}{M}\left(\ln\frac{N}{M-N}-\ln\frac{N_{0}}{M-N_{0}}\right)
		+	\end{array}</math>
		+
		+
		+	Detta ger i sin tur
		+
		+	<math>
		+	\frac{N}{M-N}=\frac{N_{0}}{M-N_{0}}\, e^{Mt/K}\quad
		+	\mbox{och}\quad N=\frac{N_{0}Me^{Mt/K}}{N_{0}(e^{Mt/K}-1)+M}.</math>
		+
		+
		+	För att kunna se vad som händer då $t\to\infty$ förkortar vi med
		+	$e^{Mt/K}$:
		+
		+	<math>
		+	N=\frac{N_{0}M}{N_{0}(1-e^{-Mt/K})+Me^{-Mt/K}}.</math>
		+
		+
		+	Eftersom $e^{-Mt/K}\to 0$ då $t\to\infty$, så får vi
		+
		+	<math>
		+	t\to\infty\text{ ger }N\to\frac{N_{0}M}{N_{0}}=M.</math>

---

Nuvarande version

[redigera] Lösningar till några övningar till lektion 19

Tillbaka till lösningarna

11.1.

Att bestämma partialbråksuppdelningar utan ansats är förstås tramsigt eftersom man i praktiken alltid använder olika ansatser. Lös därför övningen hur du vill!

11.1.a)

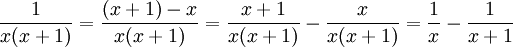
11.1.b)

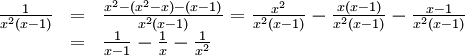
11.1.c)

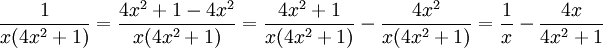
11.2.a.

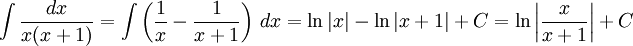
11.2.b)

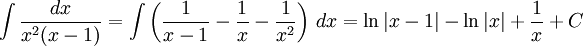
11.2.c)

11.6.a.

Vi har $9-x^2=(3+x)(3-x)$ så uppdelningen har utseendet

Vi gör liknämnigt:

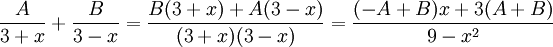
Detta ger ekvationssystemet

som har lösningen $A=B=1/2$. Partialbråksuppdelningen är således

11.6.b)

Vi faktoriserar nämnaren genom att bestämma dess nollställen:

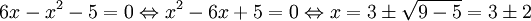
Nollställena är $x=1$ och $x=5$, så

6x − x² − 5 = − (x − 1)(x − 5) = (1 − x)(x − 5).

Partialbråksuppdelningen har utseendet

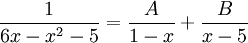
och gör vi liknämnigt så får vi

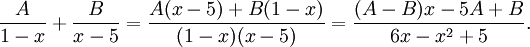
Alltså måste

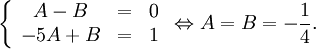
Detta ger

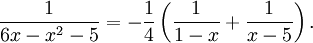
11.6.c)

Nämnaren har faktoriseringen $x^3-1=(x-1)(x^2+x+1)$, där andragradsfaktorn inte har några reella nollställen (och således inte går att faktorisera vidare). Partialbråksuppdelningen har utseendet

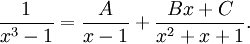
Vi gör liknämnigt i HL:

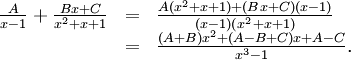
Detta ger ekvationsystemet

och vi får till sist

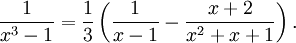
11.7.a)

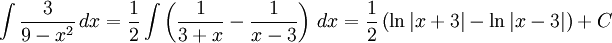
11.7.b)

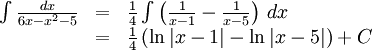
11.7.c)

Vi skriver den andra termen i parentesen som

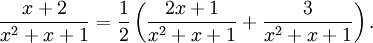
Här har den första termen utseendet $f'(x)/f(x)$, där $f(x)=x^2+x+1$. En primitiv funktion är således $\ln|f(x)|=\ln(x^2+x+1)$ (observera att $x^2+x+1>0$ för alla $x$). För att integrera den andra termen kvadratkompletterar vi nämnaren:

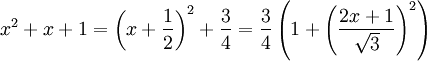
Alltså är

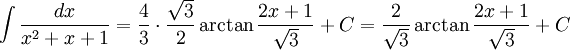
De primitiva funktionerna till $1/(x^3-1)$ är således

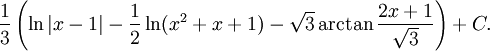
11.9.b.

Partialbråksuppdela:

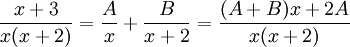
Detta ger $A+B=1$, $2A=3$, alltså $A=3/2$, $B=-1/2$. Alltså

11.9.d)

Den andra faktorn kan faktoriseras: $x^2+2x-3=(x-1)(x+3)$. Partialbråksuppdelning:

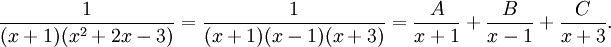
Ekvationsystemet blir

Alltså

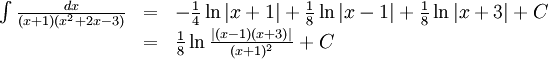
Vi har

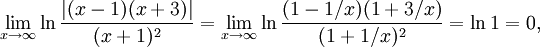
så

11.9.e)

Här är partialbråksuppdelningen

och integralen blir

11.10.

Partialbråksuppdelning ger

Detta ger i sin tur

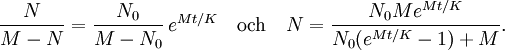
För att kunna se vad som händer då $t\to\infty$ förkortar vi med $e^{Mt/K}$:

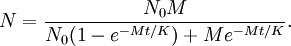
Eftersom $e^{-Mt/K}\to 0$ då $t\to\infty$, så får vi